
二离散型随机变量函数的分布教学.ppt

快乐****蜜蜂







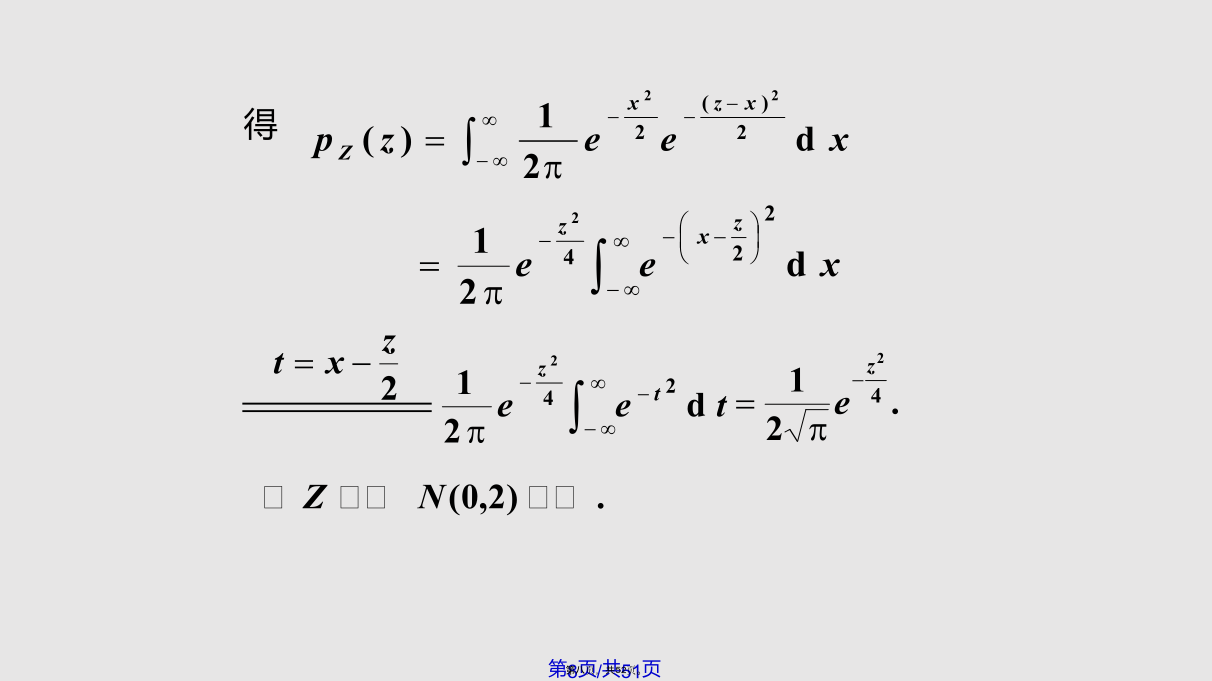


亲,该文档总共52页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

二离散型随机变量函数的分布教学.ppt
为了解决类似(lèisì)的问题,下面我们讨论两个随机变量函数的分布.例1设两个独立的随机变量X与Y的分布律为结论(jiélùn)由此可得概率密度函数为例4设两个独立(dúlì)的随机变量X与Y都服从标准正态分布,求Z=X+Y的概率密度.说明(shuōmíng)为确定积分限,先找出使被积函数不为(bùwéi)0的区域为确定积分限,先找出使被积函数(hánshù)不为0的区域同理可得当X,Y独立(dúlì)时,解得所求密度(mìdù)函数3.极值(jízhí)分布则有故有推广(tuīguǎng)若X与Y相互

二离散型随机变量函数分布.ppt
为了解决类似的问题下面我们讨论随机变量(suíjībiànliànɡ)函数的分布.二、离散(lísàn)型随机变量函数的分布概率结论(jiélùn)例2设两个独立的随机变量(suíjībiànliànꞬ)X与Y的分布律为例3设相互独立的两个随机变量X,Y具有同一分布律,且X的分布律为由此可得概率密度函数为由公式说明(shuōmíng)解此时(cǐshí)/例6证明(zhèngmíng)///同理可得当X,Y独立(dúlì)时,解得所求密度函数则有故有推广(tuīguǎng)解////四、小结(xiǎoji

离散型随机变量及分布函数.pptx
会计学二、随机变量的概念1、有些试验结果本身与数值有关(本身就是一个数).2、在有些试验中,试验结果看来与数值无关,但我们可以引进一个变量来表示它的各种结果.也就是说,把试验结果数值化.二、随机变量的概念随机变量随着试验的结果不同而取不同的值,由于试验的各个结果的出现具有一定的概率,因此随机变量的取值也有一定的概率规律.随机事件包容在随机变量这个范围更广的概念之内.或者说:随机事件是从静态的观点来研究随机现象,而随机变量则是从动态的观点来研究随机现象.例1掷一个硬币,观察出现的面,共有两个结果:例2在有两

离散型随机变量及其分布函数.ppt
一、离散型随机变量的分布函数一、离散型随机变量的分布函数实例2若随机变量X记为“连续射击,直至命中时的射击次数”,则X的可能值是:实例2随机变量X为“测量某零件尺寸时的测误差”.说明离散型随机变量的分布律也可表示为例1设一汽车在开往目的地的路上需经过四盏信号灯.每盏灯以的概率禁止汽车通过.以表示汽车首次停下时已经过的信号灯盏数(信号灯的工作是相互独立的),求的分布律.分布函数二、常见离散型随机变量的概率分布两点分布是最简单的一种分布,任何一个只有两种可能结果的随机现象,比如新生婴儿是男还是女、明天是否下雨

离散型随机变量及其分布函数.ppt
一、离散型随机变量的分布函数一、离散型随机变量的分布函数实例2若随机变量X记为“连续射击,直至命中时的射击次数”,则X的可能值是:实例2随机变量X为“测量某零件尺寸时的测误差”.说明离散型随机变量的分布律也可表示为例1设一汽车在开往目的地的路上需经过四盏信号灯.每盏灯以的概率禁止汽车通过.以表示汽车首次停下时已经过的信号灯盏数(信号灯的工作是相互独立的),求的分布律.分布函数二、常见离散型随机变量的概率分布两点分布是最简单的一种分布,任何一个只有两种可能结果的随机现象,比如新生婴儿是男还是女、明天是否下雨
