随机过程分析.pptx

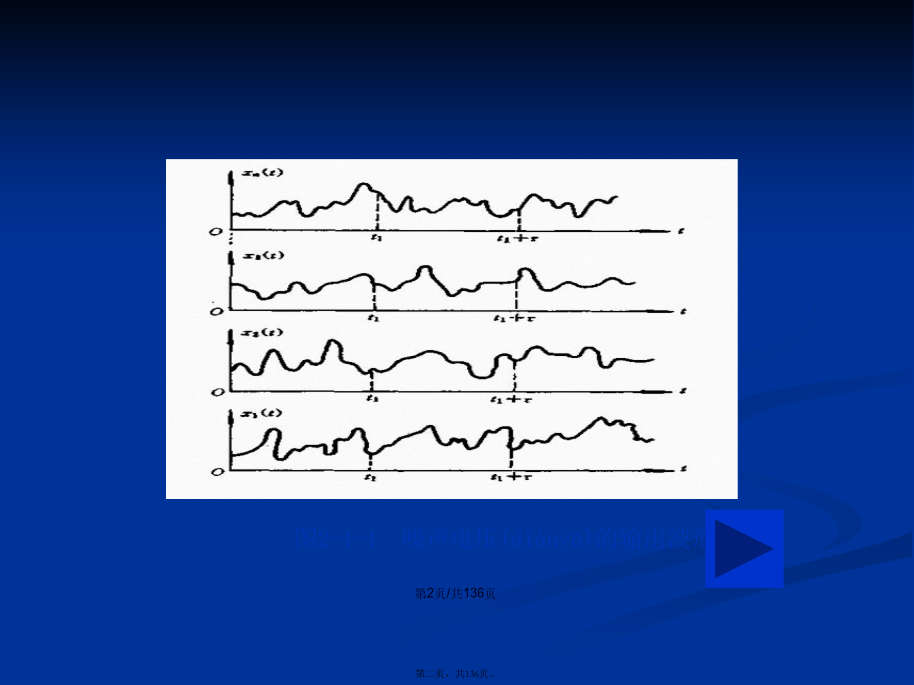
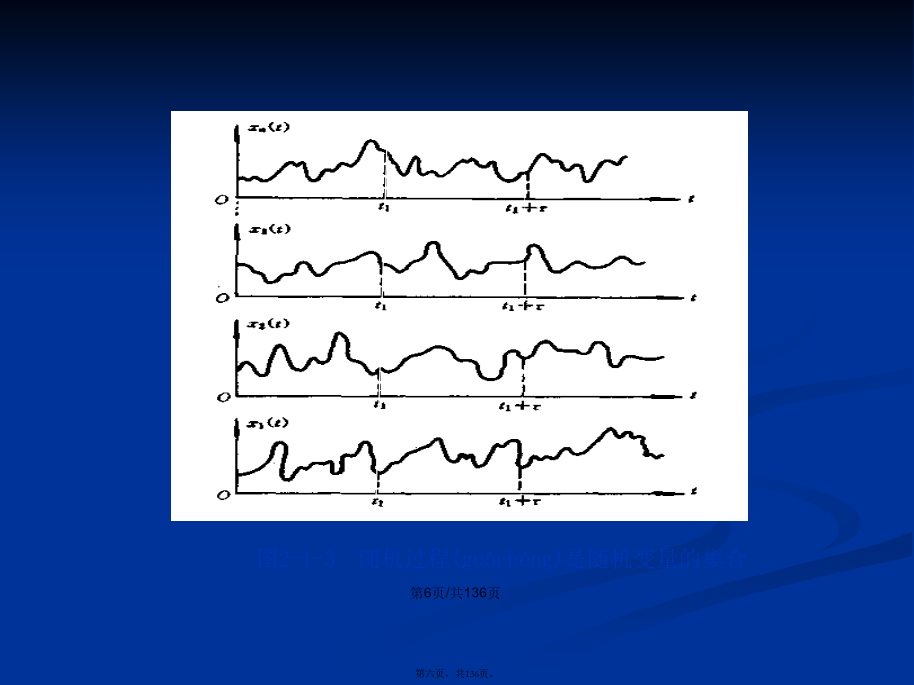
会计学图2-1-1噪声电压(diànyā)的输出波形定义1设随机试验E的样本空间为，如果对于每一个样本，总可以依某种规则确定一时间t的函数(T是时间t的变化范围)与之对应。于是，对于所有的来说，就得到一族时间t的函数，称此族时间的函数为随机过程（也称随机信号(xìnhào)）X，而族中的每一个函数称为该随机过程的样本函数。图2-1-2随机过程是样本(yàngběn)函数的集合

定义(dìngyì)2如果对于每一固定的，都是随机变量，则称是随机过程。

注：样本函数随机变量。

图2-1-3随机过程(guòchéng)是随机变量的集合因此，随机过程(guòchéng)有两种基本的表示方式：
1、样本函数集合表示(定义1)

2、随机变量集合表示(定义2)
具有(jùyǒu)以下四种含义：
1、若和都是变量，则随机过程是一族时间函数，即随机信号；
2、若是变量，而是固定值，则随机过程是一个确定的时间函数，即样本函数；
3、若是固定的，而是变量，则随机过程是一个随机变量，即样本随机变量；
4、若和都是固定值，则随机变量是一个确定值，即样本值。、随机(suíjī)过程的分类§2.2随机(suíjī)过程的统计特征统计特征也可分为：

1、幅值域描述:数学期望、方均值、方差、概率密度函数等；
2、时间(shíjiān)域描述:自相关函数、互相关函数；
3、频率域描述:自功率谱密度函数、互功率谱密度函数；
4、变换域描述：特征函数。、随机过程的概率分布

随机过程，在每一固定时刻(shíkè)，和都是随机变量。

随机事件：，

发生概率：，

1、一维分布函数
与和都有直接的关系，是和的二元函数，记为：

被称为随机(suíjī)过程的一维分布函数。
2、一维概率密度函数
如果存在二元函数，使

成立,则称为随机(suíjī)过程的一维概率密度函数,是和的二元函数，且满足
注：一维概率分布描述了随机过程在各个孤立(gūlì)时刻的统计特性。
3、二维分布函数
与，，和都有直接的关系，是，，和的四元函数，记为：

被称为随机过程的二维分布函数。
4、二维概率密度函数
如果存在四元函数，使
成立,则称为随机过程的二维概率密度函数，是，，和的四元函数，且满足

注：1、二维概率分布反映了随机过程在不同时刻的状态之间的统计特性；
2、随机过程的二维概率分布与多维随机变量(suíjībiànliànɡ)的二维概率分布所描述的物理概念是不相同的。随机过程的二维概率分布描述随机过程在不同时刻的状态之间的关系，二维随机变量(suíjībiànliànɡ)的二维概率分布则描述不同变量之间的关系。5、n维分布(fēnbù)函数和概率密度函数
例2.2讨论贝努里随机过程的一、二维概率特性。
解：贝努里随机过程，在时刻，独立地观察某个事件发生与否，建立事件的指示函数

且有概率
设，单位(dānwèi)步函数（阶跃函数）
贝努里随机过程的一维概率分布函数

一维概率密度函数

贝努里随机过程，对于不同的时刻，其随机变量是彼此统计独立的。因此，可得
贝努里随机过程的二维概率分布函数是

其中，是二维单位(dānwèi)阶跃函数。

那么二维概率密度函数

式中，
、随机过程的数字特征
随机过程的分布函数在实际上是很难获取(huòqǔ)的，甚至是不可能的。
随机过程（信号）的特征（或参数）在实际工作中运用得十分广泛。
(1)正态随机过程由数学期望和相关函数详细描述。
(2)复杂背景下目标识别、跟踪所依赖的有效依据仍然是目标在时间、空间的特征。图2-2-1云层背景(bèijǐng)下的飞机
由随机(suíjī)过程的定义2，可知随机(suíjī)过程是随机(suíjī)变量集合：1、数学期望(均值(jūnzhí)函数)
随机过程在任意时刻的取值是一随机变量，随机过程的数学期望或，即

数学期望的取值与时刻是有直接联系的，是时刻的函数。它是该随机过程在各个时刻的摆动中心。
图2-2-2随机(suíjī)过程的数学期望2、均方值
随机过程在任意时刻的取值是一随机变量(suíjībiànliànɡ)，随机过程的均方值或，即

均方值的取值与时刻是有直接联系的，是时刻的函数。
3、方差
随机过程在任意时刻的取值是一随机变量(suíjībiànliànɡ)，称随机变量(suíjībiànliànɡ)的二阶中心矩为随机过程的方差。
图2-2-3随机过程(guòchéng)的均方值、方差方差(fānɡchà)、均方值和均值有数学关系式：

方差(fānɡchà)描述在该时刻对其数学期望的偏离程度。

数学期望、均方值和均方差(fānɡchà)只能描述随机过程孤立的时间点上的统计特性。

随机过程孤立的时间点上的统计特性不能反映随机过程的起伏程度。图2-