内容提供者
几类非线性椭圆型方程的多峰解.pptx
2024-10-09
20金币
6.3MB
29页
快乐****蜜蜂
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共29页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
几类非线性椭圆型方程的多峰解.doc
几类非线性椭圆型方程的多峰解本文主要应用Lyapunov-Schmidt约化方法研究几类非线性椭圆型方程多峰解的存在性.全文共分五章：在第一章中,我们主要阐述本文所讨论问题的背景及研究现状,并简要介绍本文的主要工作.在第二章中,我们研究非线性Schrodinger方程正解的存在性,其中2<p<2N/N-2,β是一个参数,V(y)>0为满足指数衰减的权函数.当β满足一定的范围时,我们构造了上述方程非径向对称的正解.在第三章中,我们考虑方程组的分离解,其中Ω是RN中有界或者无界区域(N=1,
2024-06-11
10
13KB
几类非线性椭圆型方程的多峰解.pptx
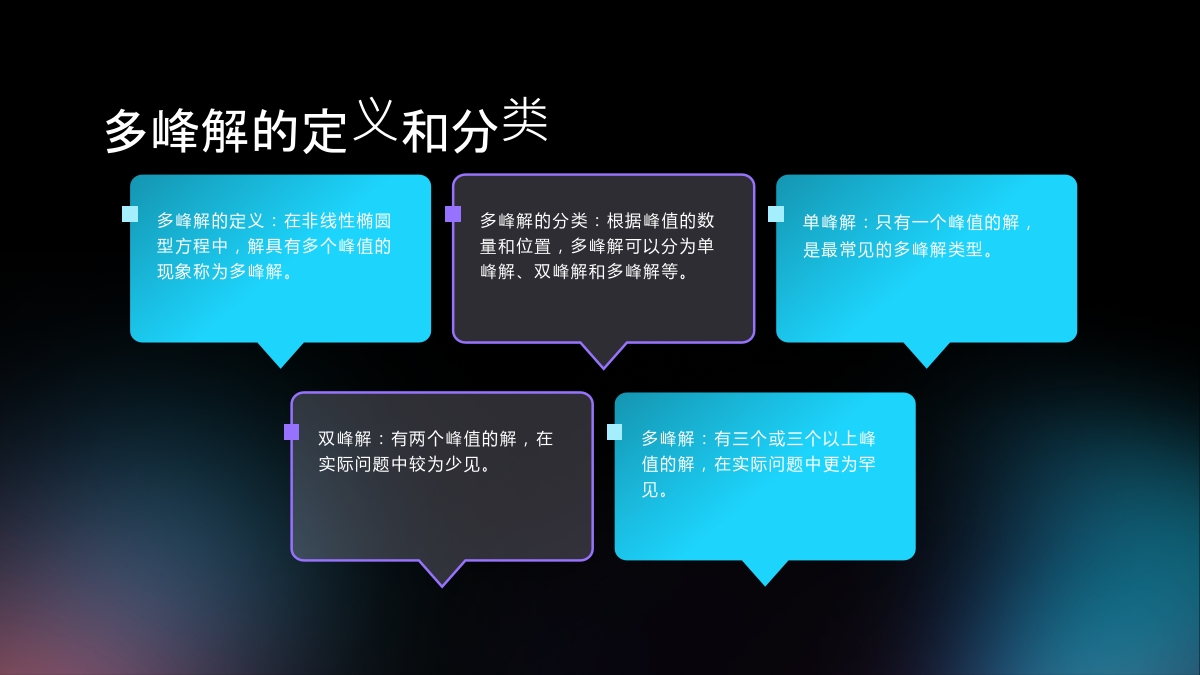
非线性椭圆型方程的多峰解目录添加章节标题非线性椭圆型方程简介方程的定义和形式方程的物理背景和应用领域求解非线性椭圆型方程的挑战多峰解的存在性和性质多峰解的定义和分类多峰解的存在性证明多峰解的数值模拟和性质分析求解非线性椭圆型方程的方法有限元方法有限差分方法谱方法边界元方法多峰解的优化和稳定性分析多峰解的优化算法多峰解的稳定性分析多峰解的动态演化过程多峰解的应用实例在流体动力学中的应用在材料科学中的应用在生态学和人口学中的应用在其他领域的应用结论与展望研究成果总结未来研究方向和展望THANKYOU
2024-10-09
20
6.3MB
几类非线性方程的多线性分离变量解.docx
几类非线性方程的多线性分离变量解非线性方程是数学中一类具有非线性项的方程，其解的求解相对于线性方程来说更加困难。非线性方程的多线性分离变量解是指能够将非线性方程转化为一组多个分离变量方程的解。本文将讨论几类常见的非线性方程，并探讨其多线性分离变量解的求解方法。1.非线性常微分方程非线性常微分方程是指方程中包含未知函数及其导数的非线性项的常微分方程。其一般形式可以表示为：dy/dx=f(x,y)其中f(x,y)为非线性函数。对于这种非线性常微分方程，可以采用变量分离法来求解其多线性分离变量解。具体步骤如下：
2024-10-15
5
10KB
几类非线性椭圆型方程解的相变和涡旋现象的研究的任务书.docx
几类非线性椭圆型方程解的相变和涡旋现象的研究的任务书一、研究背景非线性椭圆型方程广泛存在于科学和数学领域中，它们在统计物理学、化学、流体力学和生物学等领域中具有重要应用价值。这些方程通常具有复杂的解结构，这使得研究非线性椭圆型方程的解的相变和涡旋现象成为一个重要的课题。在解的相变方面，非线性椭圆型方程的解具有不同的可能性。一种情况是解的存在性和唯一性。另一种情况是解可能存在多个。在这种情况下，解的不稳定性和相互转化的相变现象是非常重要的研究方向之一。另一个研究课题是非线性椭圆方程的涡旋现象。对于某些方程来
2024-10-15
5
10KB
几类非线性椭圆型方程（组）的研究的任务书.docx
几类非线性椭圆型方程（组）的研究的任务书一、问题背景非线性椭圆型方程（组）在数学、物理、生物学等领域中都发挥着重要的作用。椭圆型方程（组）广泛应用于自然科学、工程学和经济学等领域中，因为它们在描述各种物理现象、数学模型和优化问题时具有重要的性质，如渐近稳定性、具有最小值和最大值等。非线性椭圆型方程（组）由于其更复杂和更高度非线性的特性，被广泛应用于许多实际问题中，例如分子动力学、化学反应动力学、生物生长模型、地震学、天文物理学、相场模型等领域。二、研究目的1.理论研究：研究非线性椭圆型方程（组）的解的存在
2024-09-25
5
11KB