数学建模概述.ppt

数学建模概述获奖选手心得摘录心得：让青春燃烧出最灿烂的火焰竞赛获奖证书大学里或者社会上的各种竞赛，获奖证书也非常受青睐。一名同学大学里多次参加辩论赛获奖，被一家企业老总直接聘为总裁助理；西安交大一名同学，挑战杯获奖，直接获得了麻省理工（MIT）的全奖；上海交大两名参加ACM竞赛获奖的同学，李开复直接打来电话抢先挖去；浙大一名同学大学四年不断参加各类编程比赛，累计赢得奖金20万美元，近日被topcoder聘为中国技术副总裁；等等，通过参加竞赛锻炼能力，获得证书，找到工作的例子遍地都是。开放性的数学思维
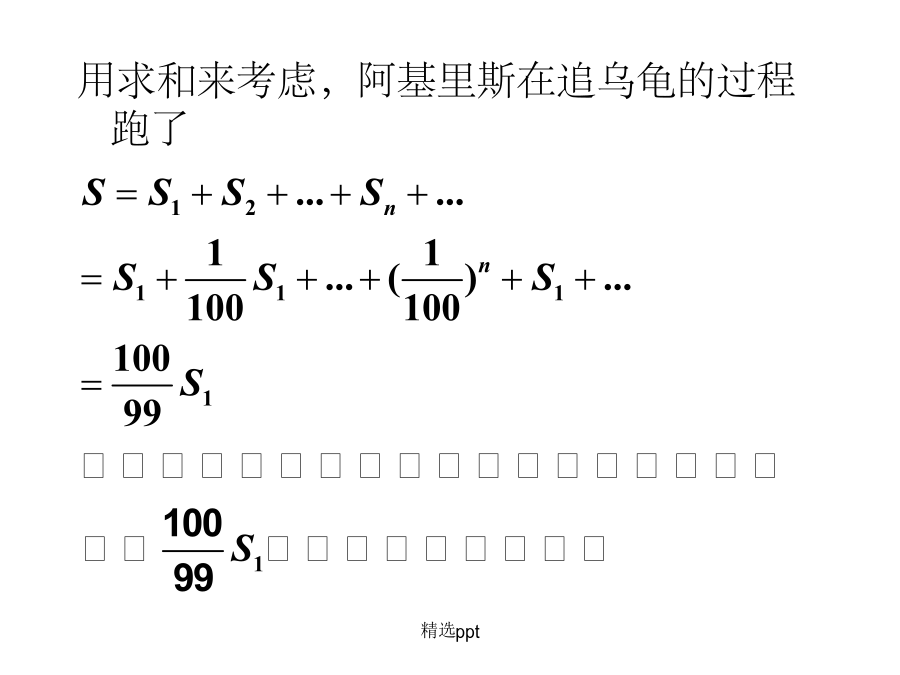
用求和来考虑，阿基里斯在追乌龟的过程跑了一位物理导师给学生出了一道试题：
请利用一个气压表来测定一座大楼的高度。

学生答道：
（1）把气压表拿到大楼的楼顶，用一条长
绳的一端栓住气压表，拉住绳子，把气压表
垂直落到地面，然后把它拉上来，测量绳子
的长度；
（2）把气压表拿到大楼的楼顶，让气压表沿
屋顶的边落下，用一块秒表测出其下落所用

的时间，然后用计算出大楼的高度。3）阴影长度比；
4）上楼过程中测出这层楼的墙有几个气压表的长度；
5）拿着气压表到地下室敲开大楼主管的门，并对他说：“主管先生，我这有一个上好的气压表，如果你告诉我这幢大楼的高度，这个气压表就是你的了。”模型：飞机模型，水电站模型，楼盘模型等是实物模型，是所研究的客观事物有关属性的模拟，它应当具有事物中我们关心和需要的重要特征。
数学模型：是指对于现实世界的某一特定对象，为了某个特定目的，作出一些必要的简化和假设，运用适当的数学工具得到一个数学结构。
假设
1）桌子四条腿一样长，桌脚与地面接触处可视为一个点，四脚的连线呈正方形。
2）地面高度是连续变化的，沿任何方向都不会出现间断，即地面可视为数学上的连续曲面。3）对于桌脚的间距和桌腿的长度而言，地面是相对平坦的，使桌子在任何位置至少又三只脚同时着地。
模型构成
要用数学语言把桌子四只脚同时着地的条件和结论表示出来。
精选ppt模型构成：安全渡河条件下的状态集合称为允许状态集合S.
状态用(1,1,1,1)表示人，狗，鸡，米在南岸，(0,0,0,0)表示人，狗，鸡，米在北岸。
允许状态集合S为:
(1,1,1,1)(0,0,0,0)
(1,0,1,1)(0,1,0,0)
(1,1,0,1)(0,0,1,0)
(1,1,1,0)(0,0,0,1)
(1,0,1,0)(0,1,0,1)决策集合：记第k次渡船上的状态
(1,0,1,0),(1,1,0,0),(1,0,0,1),(1,0,0,0)
一次过河就是一状态向量和一决策向量的加法，加法运算采用二进制（异或）
0＋0＝0，1＋0＝1，0+1=1,1+1=0
根据以上假设，人狗鸡米过河问题就转化为：找出从状态(1,1,1,1)经过奇数次决策变为状态(0,0,0,0)的系统状态转移过程。精选ppt商人安全渡河问题
三名商人各带一个随从乘船渡河，一只小船只能容纳二人，由他们自己划行，随从密约，在河的任一岸，一旦随从的人数比商人多，就杀人越货，但是如何乘船渡河的大权掌握在商人们手中，商人们怎样才能安全渡河？精选ppt精选ppt数学建模的一般步骤
模型准备
了解问题的实际背景，明确建立模型的目的掌握对象的各种信息，如统计数据等。一般要大量查阅资料请教专家。
模型假设
关键一步，要善于辨别问题的主要和次要方面，抓住主要因素，抛弃次要因素，尽量使问题均匀化线性化。建立模型
在建立模型之前，首先要明确建模的目的，因为对于同一个实际问题，出于不同的目的所建立的数学模型会有所不同。根据所给的条件和数据，建立起问题中相关变量或因素之间的数学规律,可以是数学表达式、图形和表格，或者是一个算法等。
模型求解
不同的数学模型的求解方法一般不同，除了熟练掌握一些数学知识和方法之外，还应具备在必要时针对实际问题学习新知识的能力，同时，应具备计算机操作能力，掌握一门编程语言和一两个数学工具软件包的使用。（Matlab.Lingo）
解的分析与检验
对所求出的解，必须要对解的实际意义进行分析，即模型的解在实际中说明了什么，效果怎样，模型的适用范围如何等等。同时，还要进行必要的误差分析和灵敏度分析等。
论文写作
论文要力图通俗易懂，能让人明白你用什么方法解决了什么问题，结果如何，有什么特点。
应用实际
数学模型的求解结果只有在实际中检验是合理的，才能被证明是正确的，否则，要修正模型，直到通过实际检验。数学建模与能力培养
通过学习数学建模，主要是扩大学生的知识面，培养和提高学生综合运用所学知识解决实际问题的综合能力。
具体地讲，数学建模有利于培养几个方面的能力：
1）丰富灵活的想像能力
2）抽象思维的简化能力
3）发散思维的联想能力
4）学以致用的应用能力
5）会抓重点的判断能力
6）高度灵活的综合能力