行星齿轮传动机构.ppt

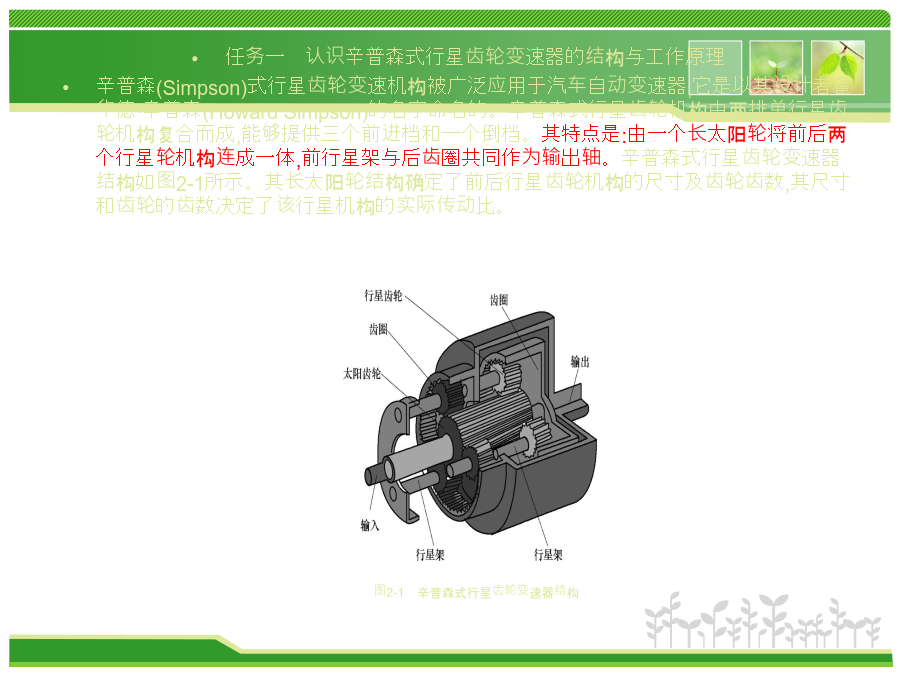
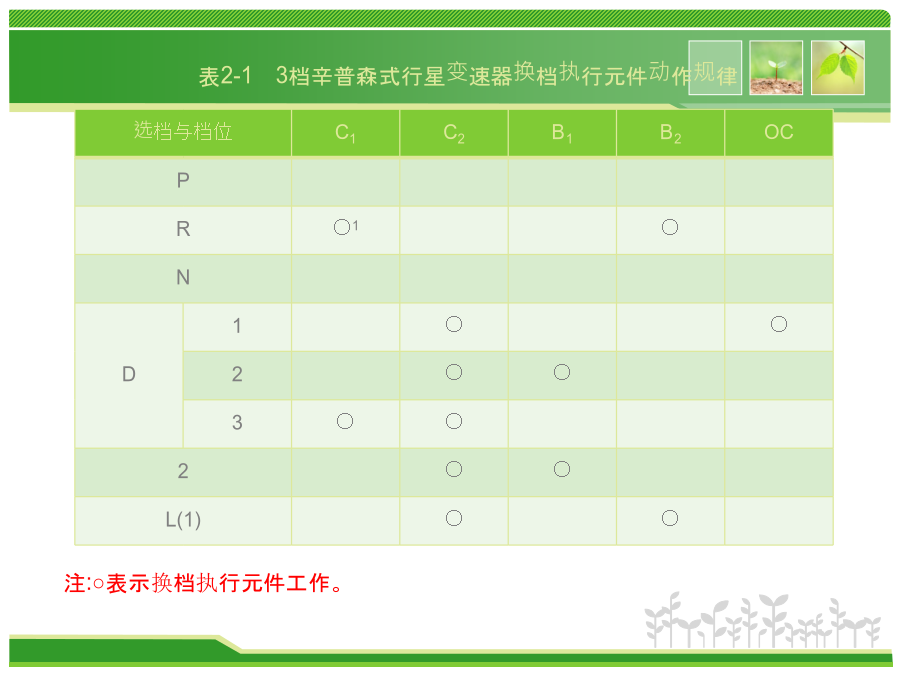
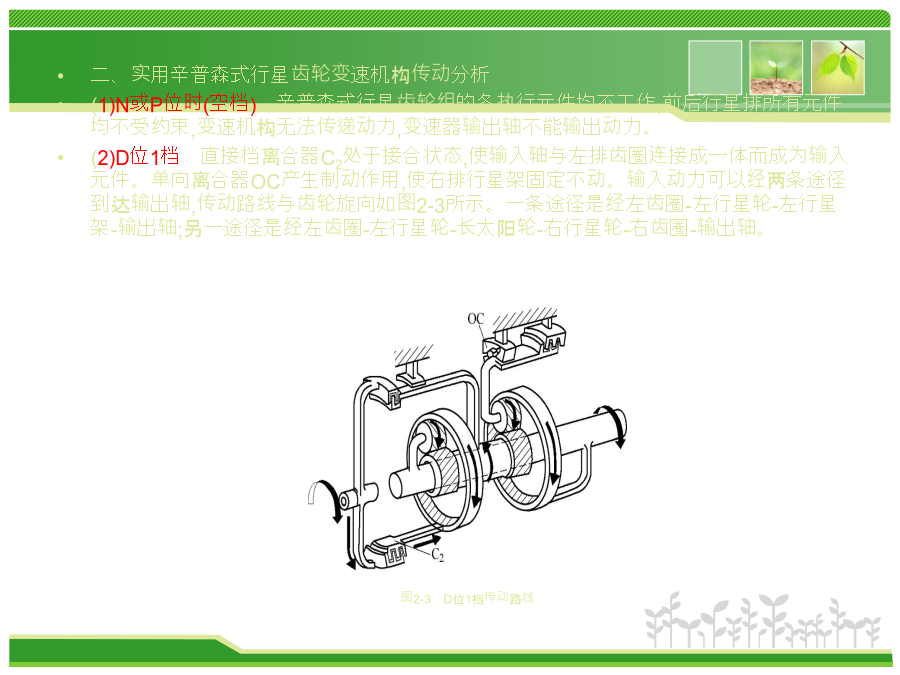
模块二
典型行星齿轮传动机构

知识目标
1.掌握辛普森式、拉维娜式行星齿轮变速器的结构。
2.理解辛普森式、拉维娜式行星齿轮变速器的工作原理。
3.了解CR-CR行星齿轮变速器的结构特点及工作原理。
技能目标
1.会分析辛普森式、拉维娜式行星齿轮变速器的动力传动并计算传动比。
2.能按照操作手册正确拆装辛普森式、拉维娜式行星齿轮变速器。由于液力变矩器的变矩系数尚无法满足汽车行驶需要,液力机械式自动变速器通常都采用齿轮式变速器作为其主要的变速装置,行星齿轮传动是最常采用的结构形式。行星齿轮变速器由行星齿轮机构和换档执行机构两部分组成。行星齿轮机构的作用是改变传动比和传动方向,即构成不同的档位。换档执行机构的作用是自动实现档位的变换。
行星齿轮式变速器具有结构简单、体积小,不需要中间轴和中间齿轮;操纵容易,各齿轮处于常啮合状态,不存在换档啮合冲击;传动比范围大等突出优点,因此行星齿轮式机构在现代轿车液力自动变速器上得到广泛应用。任务一认识辛普森式行星齿轮变速器的结构与工作原理
辛普森(Simpson)式行星齿轮变速机构被广泛应用于汽车自动变速器,它是以其设计者霍华德·辛普森(HowardSimpson)的名字命名的。辛普森式行星齿轮机构由两排单行星齿轮机构复合而成,能够提供三个前进档和一个倒档。其特点是:由一个长太阳轮将前后两个行星轮机构连成一体,前行星架与后齿圈共同作为输出轴。辛普森式行星齿轮变速器结构如图2-1所示。其长太阳轮结构确定了前后行星齿轮机构的尺寸及齿轮齿数,其尺寸和齿轮的齿数决定了该行星机构的实际传动比。但是,仅仅依靠图2-1的辛普森式行星齿轮机构还不能实现自动变速器传动比的改变,还要通过离合器、制动器和单向离合器等换档执行元件,执行一定的动作规律改变发动机动力的传递路线,最终获得与道路条件匹配的驱动力。所以自动变速器的机械结构是个传动整体,而且还要由其他的系统进行控制(液压系统、电子控制系统)。其中任一环节出现问题,都会阻碍可靠的动力传递。了解辛普森式行星齿轮的传动结构和换档原理,可以清楚地了解行星齿轮组的工作特点和动力传递路线,为理解自动变速器的换档过程提供帮助,为学习自动变速器换档控制奠定基础,也为探究整体传动中的问题分析提供思路。一、辛普森式行星齿轮变速器的结构
辛普森式行星齿轮自动变速器由两排行星齿轮机构和换档执行机构组成,图2-2a所示为三速自动变速器结构解剖图。由图2-2a可见,该机构采用两排齿轮齿数和尺寸相同的行星齿轮P1、P2,分别被称为前、后行星齿轮,构成改变传动比的基本结构。前离合器(C1)、后离合器(C2)、单向离合器(OC)、前制动器(B1)和后制动器(B2)被称为换档执行元件,作用是分别控制行星齿轮机构的不同元件,按照特定的控制逻辑将动力输入或将元件制动,以实现传动比的改变。图2-2b所示为辛普森式行星齿轮自动变速器结构简图,可将复杂的机械结构用简化的功能符号表示,表达不同元件的结构关系。图2-2c是运用简化功能符号和元件的轴测简图构成的示意图,可用来表现元件间的传动与驱动关系。
一般不同的汽车制造厂的自动变速器,结构与动作规律也不同。尽管自动变速器机械元件的基本功用相同,但在行星齿轮的主动件、从动件和固定件的设计,换档执行元件的设计有许多差别。要全面了解自动变速器,还要借助自动变速器换档执行元件动作规律表(见表2-1),才能了解哪个离合器或制动器工作时自动变速器进入哪个传动比,了解传动路线。
自动变速器换档执行元件动作规律表现的是动力传递路线的变化和该档位下必须由哪几个执行元件来实现动力传递或元件制动。该表是了解自动换档、进行传动路线分析和传动故障分析的重要依据。选档与档位二、实用辛普森式行星齿轮变速机构传动分析
(1)N或P位时(空档)辛普森式行星齿轮组的各执行元件均不工作,前后行星排所有元件均不受约束,变速机构无法传递动力,变速器输出轴不能输出动力。
(2)D位1档直接档离合器C2处于接合状态,使输入轴与左排齿圈连接成一体而成为输入元件。单向离合器OC产生制动作用,使右排行星架固定不动。输入动力可以经两条途径到达输出轴,传动路线与齿轮旋向如图2-3所示。一条途径是经左齿圈-左行星轮-左行星架-输出轴;另一途径是经左齿圈-左行星轮-长太阳轮-右行星轮-右齿圈-输出轴。因直接档离合器C2与单向离合器OC分别作用于左右两个行星机构,不易直接看出它们之间的联系。利用行星齿轮运动规律特性方程,通过联立求解,可获得该状态下的传动比与旋向。
设左排的行星机构为L,右排的行星机构为R,可建立各自的运动规律特性方程:
nL1+αnL2-(1+α)nL3=0(2-1)
nR1+αnR2-(1+α)nR3=0(2-2)
由给定条件已知:由左齿圈输入,输入转速为nL2。
因为nR3=0(已知)
由式(2