应力状态和强度理论.ppt

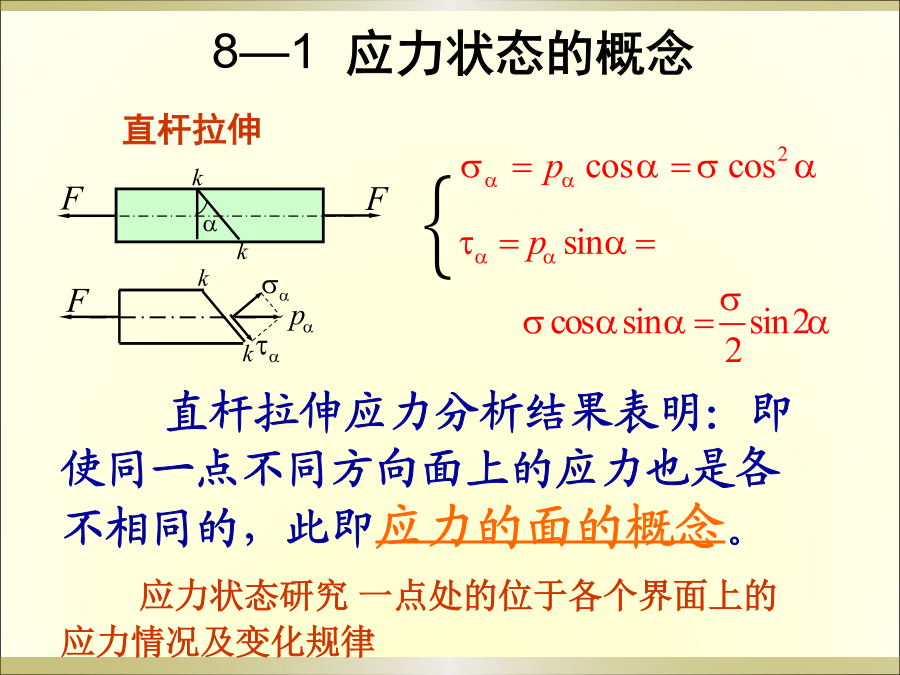
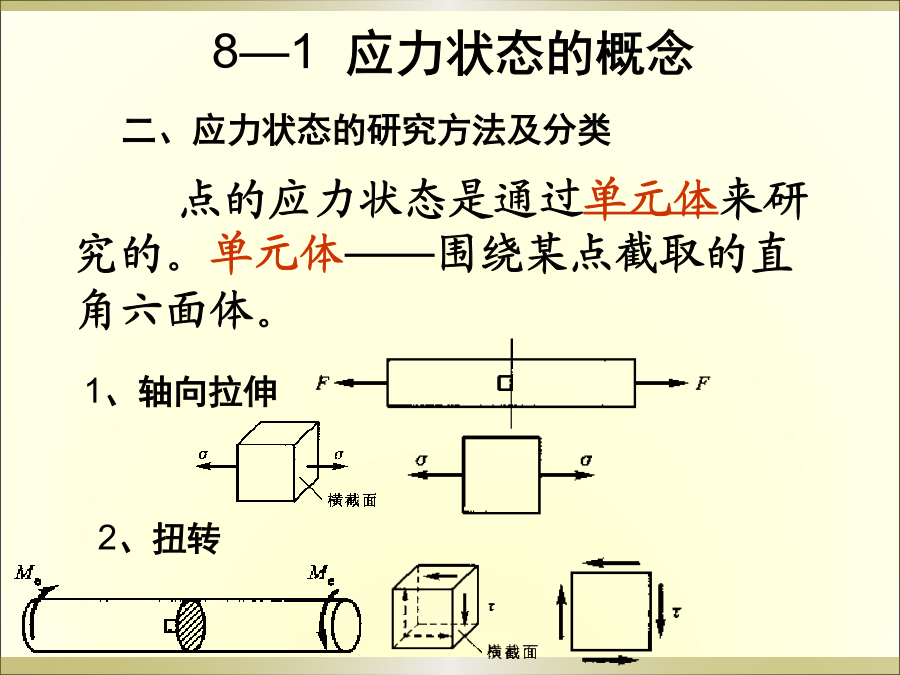
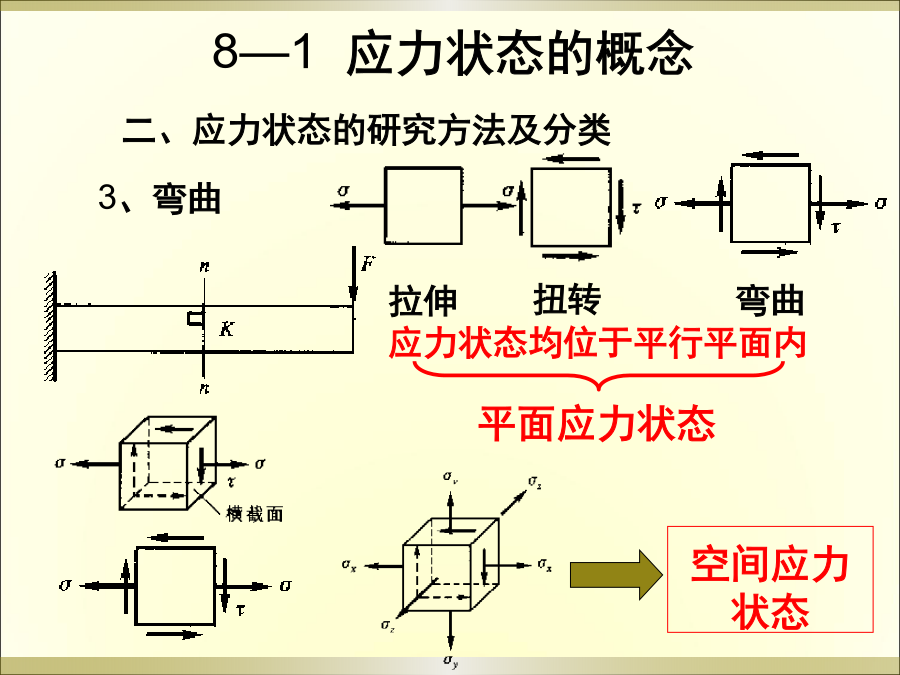
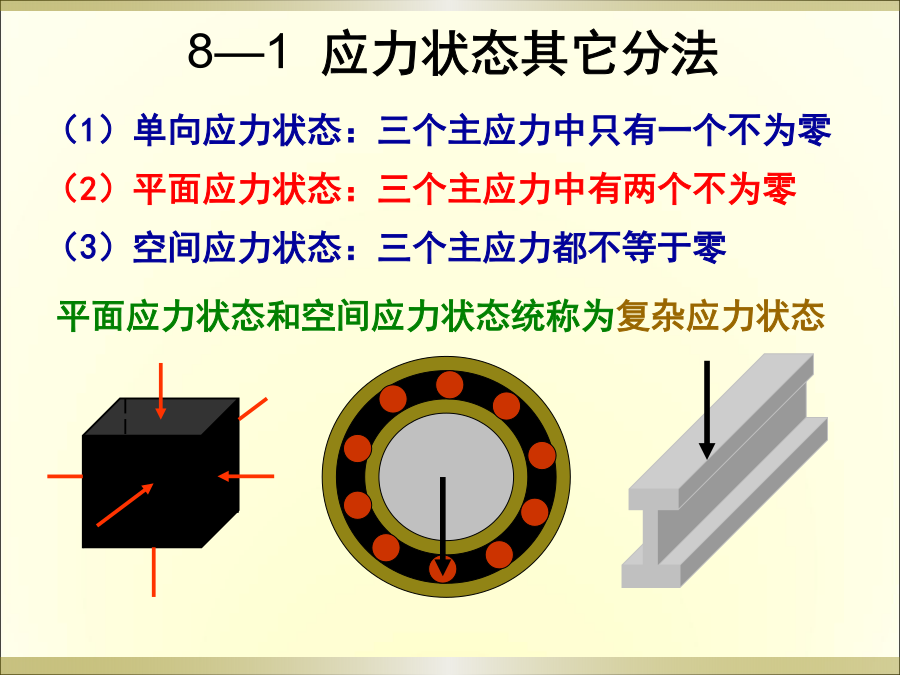
第8章

应力状态和强度理论8-1应力状态的概念
8-2平面应力状态下任意斜截面上的应力
8-3主应力和极值切应力
8-4平面应力状态下的几种特殊情况
8-6空间应力状态下任一点的主应力和最大切应力
8-7广义胡克定律
8-8强度理论横截面上正应力分析和切应力分析的结果表明：同一面上不同点的应力各不相同，此即应力的点的概念。直杆拉伸应力分析结果表明：即使同一点不同方向面上的应力也是各不相同的，此即应力的面的概念。点的应力状态是通过单元体来研究的。单元体——围绕某点截取的直角六面体。8—1应力状态的概念8—1应力状态其它分法1.斜截面上的应力列平衡方程利用三角函数公式2.正负号规则例8-1某单元体上的应力情况如图所示，a-b截面上的正应力和切应力。由8-3可以确定出两个相互垂直的平面，分别为最大正应力和最小正应力（主应力）所在平面。3.主应力的计算公式确定正应力极值试求（1）斜面上的应力；
（2）主应力、主平面；
（3）绘出主应力单元体。解：（2）主应力、主平面主平面的方位：（3）主应力单元体：按数学上极值方法确定极值切应力8-4平面应力状态下的几种特殊情况8-4平面应力状态下的几种特殊情况8-4平面应力状态下的几种特殊情况8-4平面应力状态下的几种特殊情况8-4平面应力状态下的几种特殊情况8-4平面应力状态下的几种特殊情况定义8-6空间应力状态下任一点的主应力和最大切应力8-6空间应力状态下任一点的主应力和最大切应力8-6空间应力状态下任一点的主应力和最大切应力8-6空间应力状态下任一点的主应力和最大切应力1.基本变形时的胡克定律2、三向应力状态的广义胡克定律－叠加法8-7广义胡克定律3、广义胡克定律的一般形式8-7广义胡克定律例8-7某点应力状态如图所示，已知σx=30MPa，σy=-40MPa，τx=20MPa，E=2×105MPa，μ=0.3，试求该点沿σx方向的线应变εx。（拉压）强度理论：
人们根据大量的破坏现象，通过判断推理、概括，提出了种种关于破坏原因的假说，找出引起破坏的主要因素，经过实践检验，不断完善，在一定范围与实际相符合，上升为理论。构件由于强度不足将引发两种失效形式1.最大拉应力理论（第一强度理论）断裂条件2.最大伸长线应变理论（第二强度理论）实验表明：此理论对于一拉一压的二向应力状态的脆
性材料的断裂较符合，如铸铁受拉压比第一强度理论
更接近实际情况。无论材料处于什么应力状态,只要发生屈服,都是由于微元内的最大切应力达到了某一极限值。屈服条件实验表明：此理论对于塑性材料的屈服破坏能够得到
较为满意的解释。并能解释材料在三向均压下不发生
塑性变形或断裂的事实。无论材料处于什么应力状态,只要发生屈服,都是由于微元的最大形状改变比能(单位体积应变能）达到一个极限值。强度理论的统一表达式：例题8-2（1）