
应力状态分析.ppt

lj****88





亲,该文档总共70页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

应力状态分析.pdf

应力状态分析.ppt
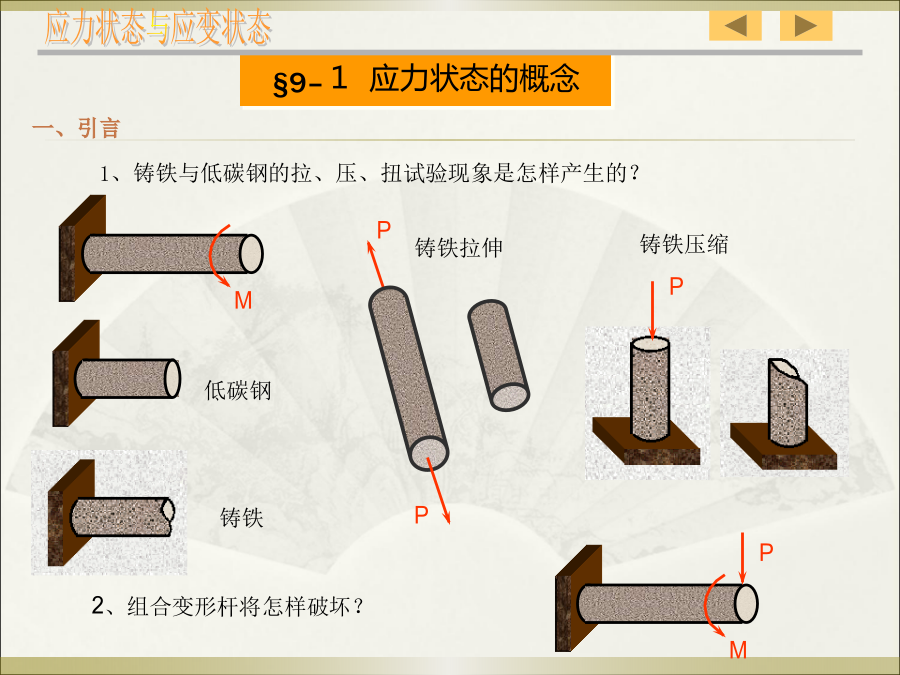
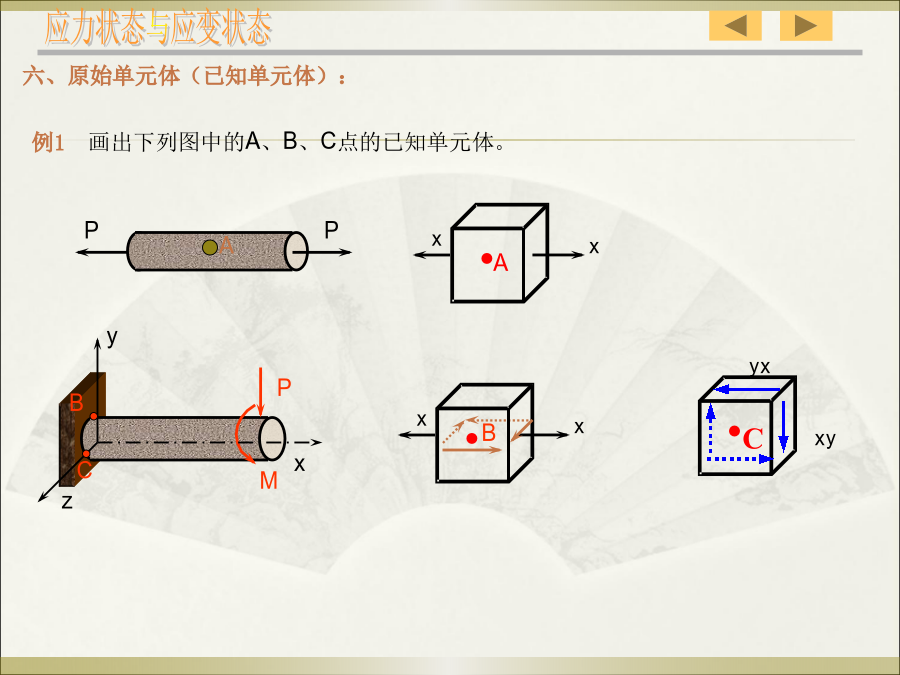
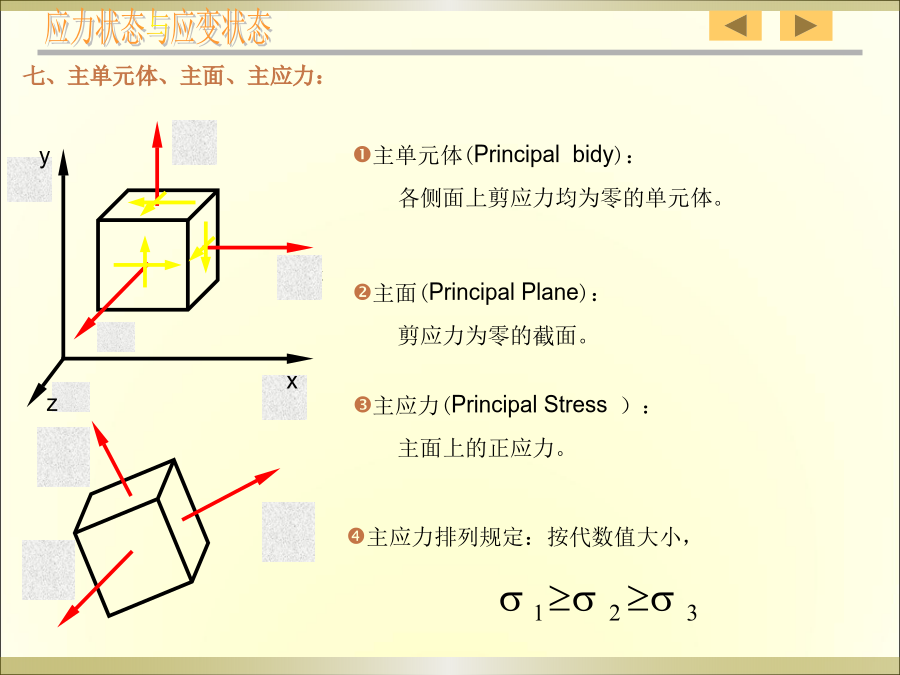
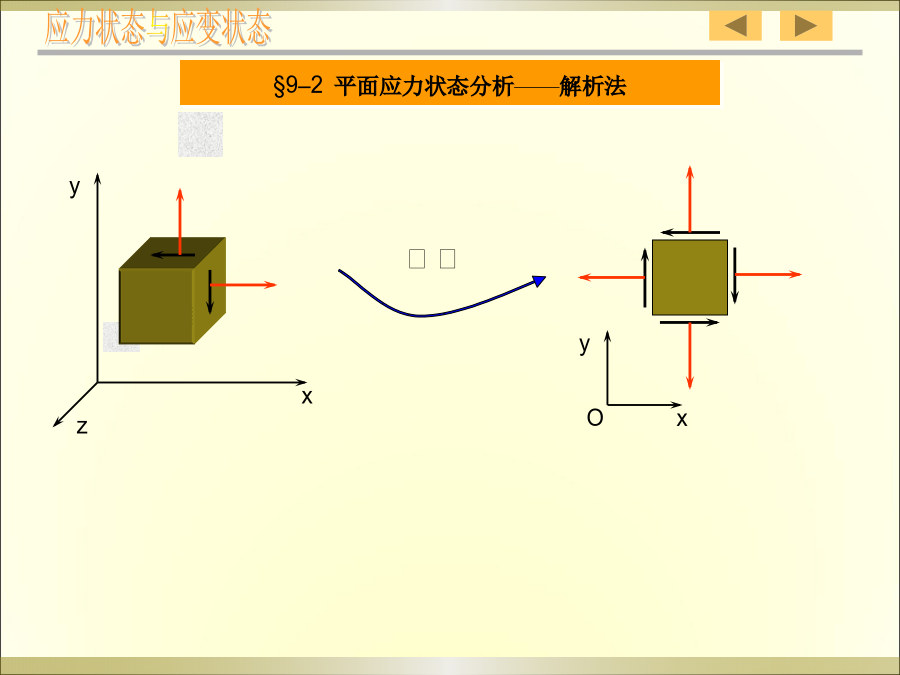
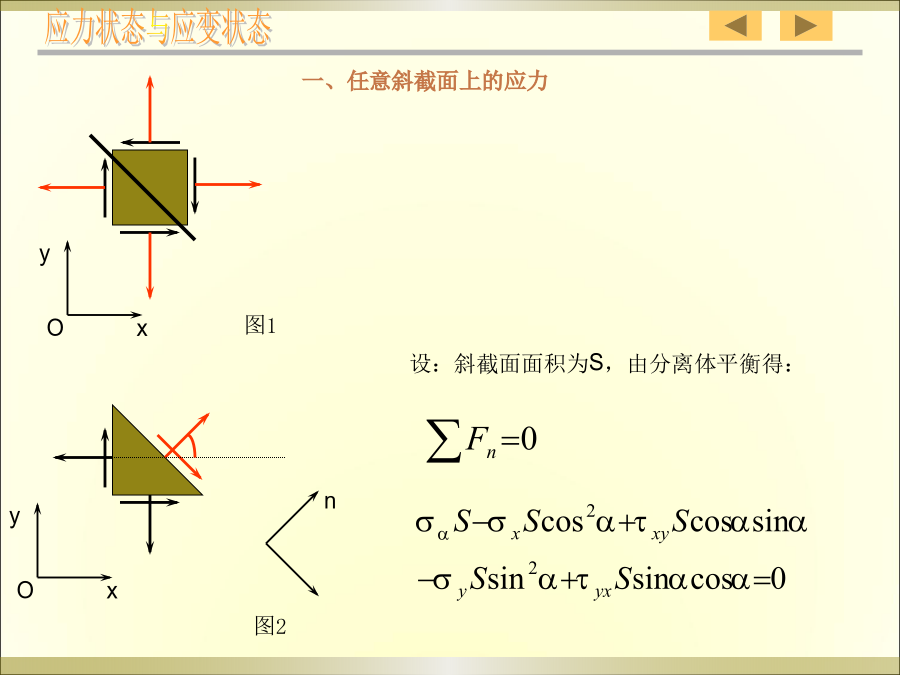
第九章应力状态分析和强度理论§9–1应力状态的概念tzx七、主单元体、主面、主应力:单向应力状态(UnidirectionalStateofStress):一个主应力不为零的应力状态。§9–2平面应力状态分析——解析法规定:截面外法线同向为正;ta绕研究对象顺时针转为正;a逆时针为正。图1二、极值应力x例2分析受扭构件的破坏规律。破坏分析§9–3平面应力状态分析——图解法建立应力坐标系,如下图所示,(注意选好比例尺)应力状态与应变状态四、在应力圆上标出极值应力解法2—解析法:分析——建立坐

应力状态分析.ppt
第九章应力状态分析和强度理论§9–1应力状态的概念tzx七、主单元体、主面、主应力:单向应力状态(UnidirectionalStateofStress):一个主应力不为零的应力状态。§9–2平面应力状态分析——解析法规定:截面外法线同向为正;ta绕研究对象顺时针转为正;a逆时针为正。图1二、极值应力x例2分析受扭构件的破坏规律。破坏分析§9–3平面应力状态分析——图解法建立应力坐标系,如下图所示,(注意选好比例尺)应力状态与应变状态四、在应力圆上标出极值应力解法2—解析法:分析——建立坐

应力状态分析.ppt
第九章应力状态分析和强度理论§9–1应力状态的概念tzx七、主单元体、主面、主应力:单向应力状态(UnidirectionalStateofStress):一个主应力不为零的应力状态。§9–2平面应力状态分析——解析法规定:截面外法线同向为正;ta绕研究对象顺时针转为正;a逆时针为正。图1二、极值应力x例2分析受扭构件的破坏规律。破坏分析§9–3平面应力状态分析——图解法建立应力坐标系,如下图所示,(注意选好比例尺)应力状态与应变状态四、在应力圆上标出极值应力解法2—解析法:分析——建立坐

应力状态分析.doc
应力状态分析一、概念题1.判断题:(以下结论对者画√,错者画×)(1)单元体内的主平面不一定就是三个。也可能有无数个。()(2)第1主应力是单元体内绝对值最大的正应力。()(3)受扭圆轴横截面上的点只有切应力,因而均处于单向应力状态。()(4)如微元体处于纯剪切应力状态,因而微元体内任何方向的斜截面上均没有正应力。()(5)凡是产生组合变形的杆件上的点,均处于复杂应力状态。()(6)扭转与弯曲组合变形的杆件,从其表层取出的微元体处于二向应力状态。()(7)扭转与弯曲组合变形的杆件,在其横截面上仍能取得处于
