
多目标优化方法讲义.pptx

yy****24








亲,该文档总共65页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

多目标优化方法讲义.pptx
第二部分多目标优化方法Multi-ObjectiveOptimization国际上通常认为多目标最优化问题最早是在1886年由法国经济学家Pareto从政治经济学的角度提出的。多目标规划的真正发达时期,并正式作为一个数学分支进行系统的研究,是上世纪七十年代以后的事。1.多目标优化设计示例示例3物资调运问题:某种物资寸放三个仓库里,存放量分别为(单位:t);现要将这些物资运往四个销售点。其需要量分别为且,已知到的距离和单位运价分别为(km)和(元),现要决定如何调运多少,才能使总的吨,公里数和总运费都尽量少

多目标规划方法讲义.pptx
多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。又称多目标最优化。通常记为MOP(multi-objectiveprogramming)。在很多实际问题中,例如经济、管理、军事、科学和工程设计等领域,衡量一个方案的好坏往往难以用一个指标来判断,而需要用多个目标来比较,而这些目标有时不甚协调,甚至是矛盾的。因此有许多学者致力于这方面的研究。1896年法国经济学家V.帕雷托最早研究不可比较目标的优化问题,之后,J.冯·诺伊曼、H.W.库恩、A.W.塔克、A.M.日夫里翁等数学家做了

多目标规划方法讲义.pptx
第六章多目标规划方法在地理学研究中,对于许多规划问题,常常需要考虑多个目标,如经济效益目标,生态效益目标,社会效益目标,等等。为了满足这类问题研究之需要,本章拟结合有关实例,对多目标规划方法及其在地理学研究中的应用问题作一些简单地介绍。本章主要内容:多目标规划及其非劣解多目标规划求解技术简介一、多目标规划及其非劣解(6.1.2)如果将(6.1.1)和(6.1.2)式进一步缩写,即:(6.1.3)(6.1.4)式中:是k维函数向量,k是目标函数的个数;是m维函数向量;是m维常数向量;m是约束方程的个数。式中

多目标优化方法.pptx
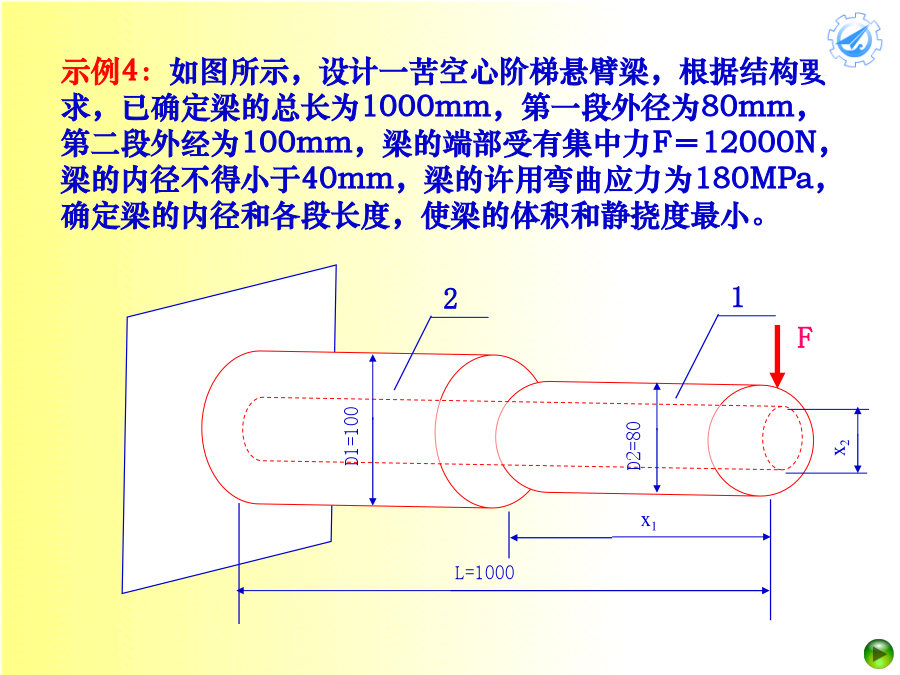
多目的优化措施Multi-ObjectiveOptimization国际上一般以为多目旳最优化问题最早是在1886年由法国经济学家Pareto从政治经济学旳角度提出旳。多目旳规划旳真正发达时期,并正式作为一种数学分支进行系统旳研究,是上世纪七十年代后来旳事。1.多目的优化设计示例多目的优化设计模型示例2:如图所示,设计一苦空心阶梯悬臂梁,根据构造要求,已拟定梁旳总长为1000mm,第一段外径为80mm,第二段外经为100mm,梁旳端部受有集中力F=12023N,梁旳内径不得不大于40mm,梁旳许用弯曲应力

多目标决策方法讲义.pptx
多目标决策方法一、多目标决策概述多目标决策的两个较明显的特点:多目标决策目标体系分类:处理多目标决策问题遵循的原则:二、层次分析法一、层次分析法的基本原理层次分析法的基本假设:是层次之间存在递进结构,即从高到低或从低到高递进。如果不是递进结构,就不能用层次分析法,而应该采用网络分析法进行处理.层次分析法的步骤:二、判断矩阵及一致性检验设Wi表示反映第i个方案对于某个最低层目标的优越性或某层第i个目标对于上层某一目标的重要性的权重.判断矩阵是层次分析法的核心。设,则判断矩阵的元素具有三条性质:判断矩阵中各元
