
11线性方程组的迭代法-雅可比、高斯塞德尔和超松弛迭代PPT课件.ppt

lj****88









亲,该文档总共55页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

11线性方程组的迭代法-雅可比、高斯塞德尔和超松弛迭代PPT课件.ppt
§6.1迭代法的基本思想迭代法的基本思想是将线性方程组转化为便于迭代的等价方程组,对任选一组初始值,按某种计算规则,不断地对所得到的值进行修正,最终获得满足精度要求的方程组的近似解。设非奇异,,则线性方程组有惟一解,经过变换构造出一个等价同解方程组将上式改写成迭代式如果存在极限则称迭代法是收敛的,否则就是发散的。收敛时,在迭代公式中当时,,则,故是方程组的解。对于给定的方程组可以构造各种迭代公式。并非全部收敛例1用迭代法求解线性方程组§6.2雅可比与高斯-塞德尔迭代法§6.2.1雅可比迭代法算法取初始向量

雅可比迭代法与高斯塞德尔迭代法综述.docx
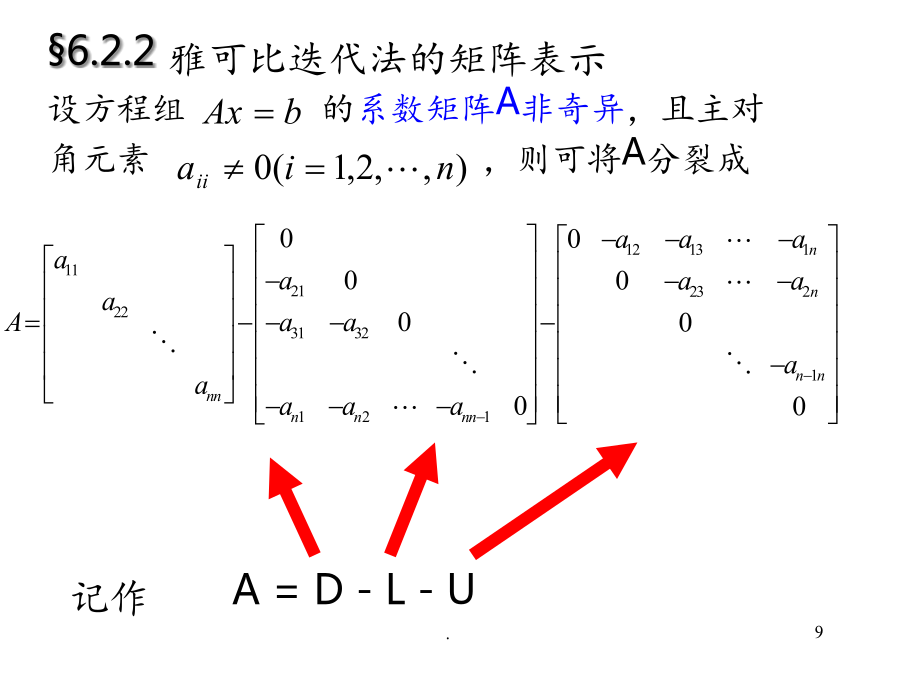
第八节雅可比迭代法与高斯—塞德尔迭代法一雅可比迭代法设线性方程组(1)的系数矩阵A可逆且主对角元素均不为零,令并将A分解成(2)从而(1)可写成令其中.(3)以为迭代矩阵的迭代法(公式)(4)称为雅可比(Jacobi)迭代法(公式),用向量的分量来表示,(4)为(5)其中为初始向量.由此看出,雅可比迭代法公式简单,每迭代一次只需计算一次矩阵和向量的乘法.在电算时需要两组存储单元,以存放及.例1用雅可比迭代法求解下列方程组解将方程组按雅可比方法写成取初始值按迭代公式进行迭代,其计算结果如表1所示表10123

八节雅可比与高斯—塞德尔迭代法PPT课件.ppt
生成向量序列{x(k)},若序列{x(k)}的收敛条件,收敛速度,误差估计等。其中aii0(i=1,2,…,n)建立迭代格式于是雅可比迭代法可写为矩阵形式例如已知线性方程组Ax=b的矩阵为在Jacobi迭代中,计算xi(k+1)(2in)时,使用xj(k+1)代替xj(k)(1ji-1),即或缩写为例如已知线性方程组Ax=b的矩阵为例1用雅可比迭代法解方程组k解:Gauss-Seidel迭代格式为2024/2/9取x(0)=(0,0,0)T计算如下:定理1在下列任一条件下,雅克比迭代法收敛。定理

用雅可比迭代法和高斯赛德尔迭代法解线性方程组.docx
西安财经学院本科实验报告学院(部)统计学院实验室数学专业实训基地课程名称大学数学实验学生姓名董童丹(编程)杨媚(实验报告)学号08042801250804280126专业数学与应用数学0801教务处制二0一一年五月四日《用雅可比迭代法和高斯赛德尔迭代法解线性方程组》实验报告开课实验室:实验室3132011年5月4日学院统计学院年级、专业、班数学与应用数学0801班姓名董童丹杨媚成绩课程名称大学数学实验实验项目名称用雅可比迭代法和高斯赛德尔迭代法解线性方程组指导教师严惠云教师评语教师签名:年月日一、实验目的

雅可比,高斯-赛德尔以及SOR迭代法.doc
昨天闲来无事,就把雅可比,高斯-赛德尔和SOR迭代法解方程组的程序写了.把主要程序发了,可能有谁用的着./**********雅可比迭代法**********/voidJacobi(floatxk[]){inti,j;floatt=0.0;floattt=0.0;float*xl;xl=(float*)malloc(sizeof(float)*(n+1));for(i=1;i<n+1;i++){floatt=0.0;for(j=1;j<n+1;j++){if(j==i)continue;t=t+a[i][
