
蒙特卡罗模拟方法.ppt

15****92





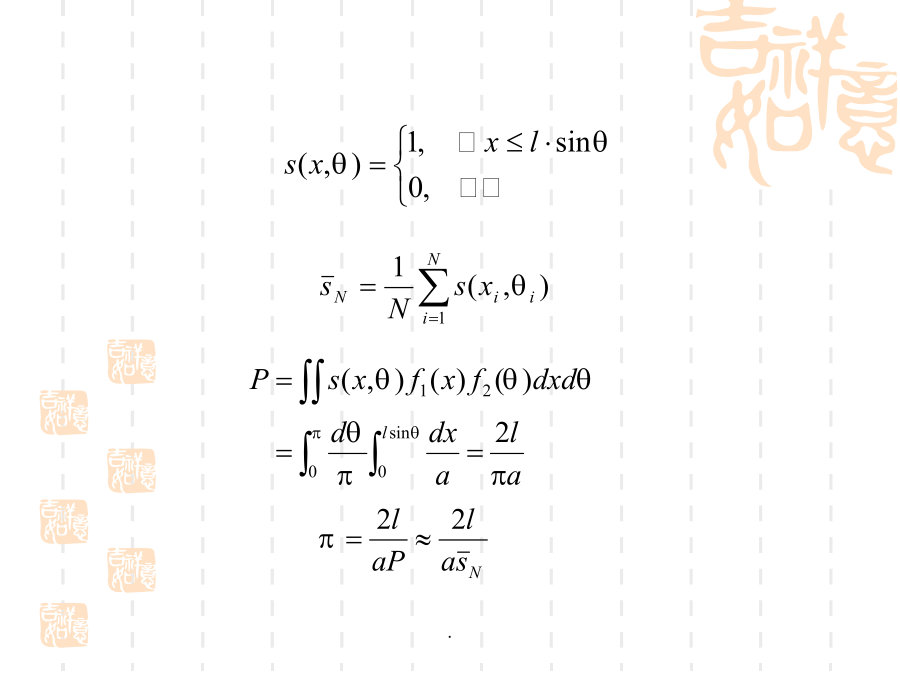




亲,该文档总共78页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

蒙特卡罗模拟方法.ppt
蒙特卡罗模拟方法蒙特卡罗模拟方法MonteCarlo方法的发展历史1777年,古稀之年的蒲丰在家中请来好些客人玩投针游戏(针长是线距之半),他事先没有给客人讲与π有关的事。客人们虽然不知道主人的用意,但是都参加了游戏。他们共投针2212次,其中704次相交。蒲丰说,2212/704=3.142,这就是π值。这着实让人们惊喜不已。例.蒲丰氏问题一些人进行了实验,其结果列于下表:20世纪四十年代,由于电子计算机的出现,利用电子计算机可以实现大量的随机抽样的试验,使得用随机试验方法解决实际问题才有了可能。其中作

蒙特卡罗模拟方法ppt课件.ppt
蒙特卡罗模拟方法蒙特卡罗模拟方法MonteCarlo方法的发展历史1777年,古稀之年的蒲丰在家中请来好些客人玩投针游戏(针长是线距之半),他事先没有给客人讲与π有关的事。客人们虽然不知道主人的用意,但是都参加了游戏。他们共投针2212次,其中704次相交。蒲丰说,2212/704=3.142,这就是π值。这着实让人们惊喜不已。例.蒲丰氏问题一些人进行了实验,其结果列于下表:20世纪四十年代,由于电子计算机的出现,利用电子计算机可以实现大量的随机抽样的试验,使得用随机试验方法解决实际问题才有了可能。其中作

数模-随机模拟-蒙特卡罗方法.ppt
随机模拟—蒙特卡罗方法(MonteCarlo)蒙特卡罗(MonteCarlo)方法随机模拟—MonteCarlo方法1.蒙特卡罗方法概述蒙特卡罗方法的基本思想例1.蒲丰氏问题一些人进行了实验,其结果列于下表:例2.射击问题(打靶游戏)现假设该运动员进行了N次射击,每次射击的弹着点依次为r1,r2,…,rN,则N次得分g(r1),g(r2),…,g(rN)。其算术平均值为代表了该运动员的成绩。换言之,为积分<g>的估计值,或近似值。在该例中,用N次试验所得成绩的算术平均值作为数学期望<g>的估计值(积分近似

蒙特卡罗方法.doc
蒙特卡罗方法“读一读”中提到的蒙特卡罗方法是以概率和统计的理论、方法为基础的一种计算方法它将所求解的问题与一定的概率模型相联系用计算机实现统计模拟或抽样以获得问题的近似解因此又称为统计模拟法或统计试验法.蒙特卡罗是摩纳哥的一个城市以赌博闻名于世.蒙特卡罗方法借用这一城市的名称是为了象征性地表明该方法的概率统计特点.作为一种计算方法蒙特卡罗方法是由乌拉姆(S.M.Ulam.1909-1984)和冯·诺伊曼(J.vonNeumann1903-1957)在20世纪40年代为研制核武器的需要而首先提出

蒙特卡罗方法.pptx
会计学5.1基本思想和一般过程蒙特卡罗方法5.1基本思想和一般过程长度为l的针随机地落在相距为d>l的一组水平线之间,求针与线相交的概率?针相对于平行线的位置可以用一个随机向量表示随机向量平均分布在区间[0,d)×[0,).其概率密度函数为1/d.针与平行线相交的概率为5.1基本思想和一般过程5.1基本思想和一般过程5.1基本思想和一般过程5.1基本思想和一般过程5.1基本思想和一般过程5.1基本思想和一般过程5.1基本思想和一般过程5.2随机数和伪随机数5.2随机数和伪随机数5.2随机数和伪随机数5
