
有限差分法基础.pptx

骑着****猪猪









亲,该文档总共61页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
《有限差分法基础》第1章 有限差分法 绪论.ppt
《有限差分法基础》24课时/1.5学分某公司铸件铸造工艺方案模拟实例一、主要内容二、考试方式:平时考勤30%+卷面考试70%。(评分比例暂定)(注意:闭卷考试!)三、考题类型(暂定)1.简答题6×102.论述题1×40参考资料IntroductionofFiniteDifferenceMethodCAE技术基础铸造CAE技术基础铸造CAE技术基础铸造CAE技术基础铸造CAE技术基础大型风电轮毂球铁件凝固液相前沿变化13传热分析整体实例——泵体充型凝固全过程模拟铸钢件泵体工艺的STL三维模型色温填充动画1/

有限差分法基础.ppt
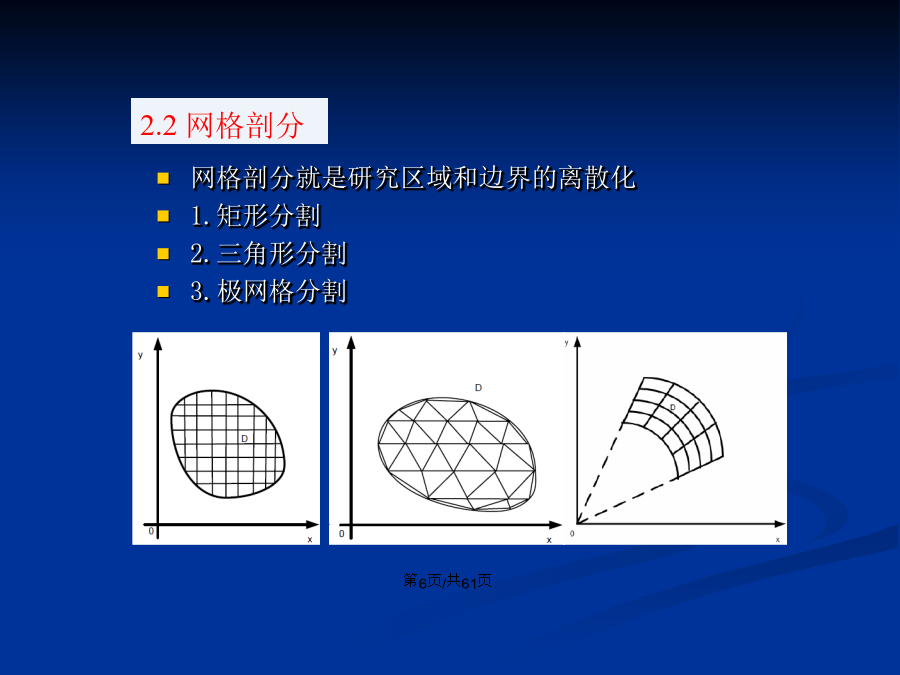
第二章有限差分法第二章有限差分法1.地球内部介质,不仅存在纵向非均匀结构(一维地球模型),也存在横向非均匀结构(不同块体、断层系统);2.几何模型也呈现出相当的复杂性;3.另外,边界条件和初始条件对于不同问题具有特殊性。对于存在复杂介质和几何、特殊边界条件和初始条件的实际地质问题,一般不存在解析解,需要近似的数值求解方法。有限差分方法是地球物理方法中最常见的一种。有限差分法以变量离散取值后对应的函数值来近似微分方程中独立变量的连续取值。我们放弃了微分方程中独立变量可以取连续值的特征,而关注独立变量离散取值

有限差分法基础.ppt
第二章有限差分法第二章有限差分法1.地球内部介质,不仅存在纵向非均匀结构(一维地球模型),也存在横向非均匀结构(不同块体、断层系统);2.几何模型也呈现出相当的复杂性;3.另外,边界条件和初始条件对于不同问题具有特殊性。对于存在复杂介质和几何、特殊边界条件和初始条件的实际地质问题,一般不存在解析解,需要近似的数值求解方法。有限差分方法是地球物理方法中最常见的一种。有限差分法以变量离散取值后对应的函数值来近似微分方程中独立变量的连续取值。我们放弃了微分方程中独立变量可以取连续值的特征,而关注独立变量离散取值

有限差分法基础.pptx
会计学1.地球内部介质,不仅存在纵向非均匀结构(一维地球模型),也存在横向非均匀结构(不同块体、断层系统);2.几何模型也呈现出相当的复杂性;3.另外,边界条件和初始条件对于不同问题具有特殊性。对于存在复杂介质和几何、特殊边界条件和初始条件的实际地质问题,一般不存在解析解,需要近似的数值求解方法。有限差分方法是地球物理方法中最常见的一种。有限差分法以变量离散取值后对应的函数值来近似微分方程中独立变量的连续取值。我们放弃了微分方程中独立变量可以取连续值的特征,而关注独立变量离散取值后对应的函数值。有限差分法

有限元与有限差分法基础.ppt
有限元法基础及有限差分法基础有限元法基础有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想离散化过程离散化过程离散化过程离散化过程单元刚度矩阵的特性线弹性问题几何方程—三维问题线弹性问题几何方程—二维问题线弹性问题几何方程—二维问题线弹性问题几何方程—一维问题线弹性问题本构方程—三维问题线弹性问题本构方程—平面应力线弹性问题本构方程—平面应力线弹性问题本构方程
