有限元与有限差分法基础.ppt

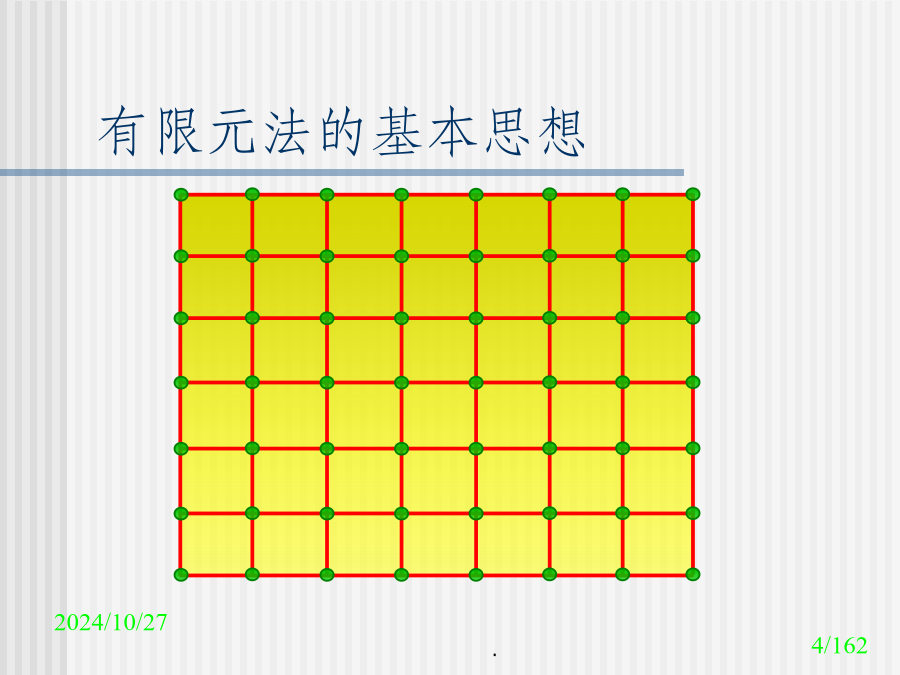
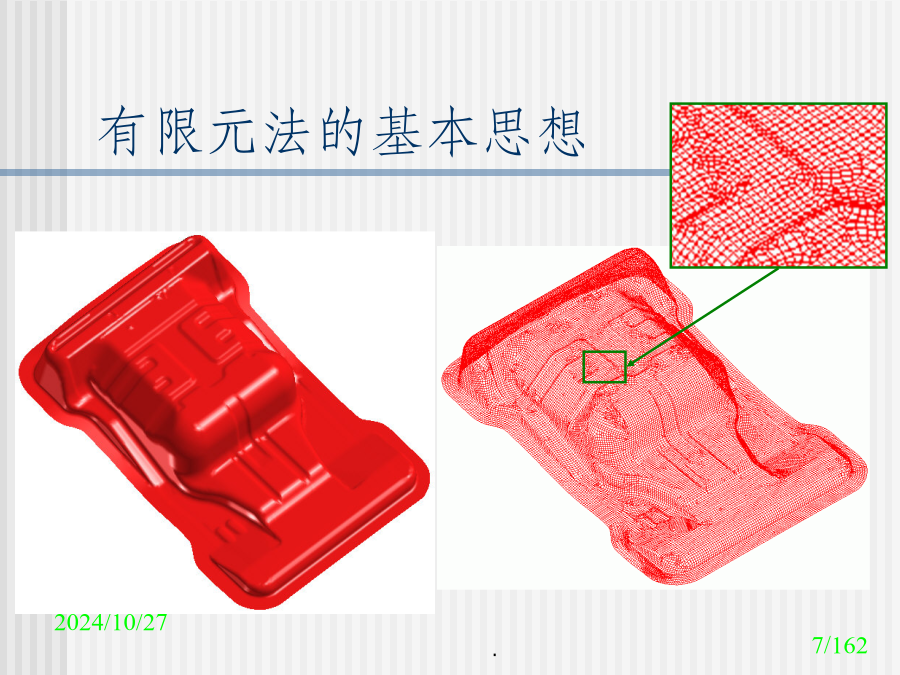
有限元法基础及有限差分法基础有限元法基础有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想有限元法的基本思想离散化过程离散化过程离散化过程离散化过程单元刚度矩阵的特性线弹性问题几何方程—三维问题线弹性问题几何方程—二维问题线弹性问题几何方程—二维问题线弹性问题几何方程—一维问题线弹性问题本构方程—三维问题线弹性问题本构方程—平面应力线弹性问题本构方程—平面应力线弹性问题本构方程—平面应变线弹性问题本构方程—平面应变线弹性问题本构方程—轴对称线弹性问题本构方程—轴对称线弹性问题本构方程—轴对称线弹性问题本构方程—一维问题常用单元模型常用单元模型常用单元模型常用单元模型常用单元模型常用单元模型常用单元模型常用单元模型常用单元模型常用单元模型常用单元模型常用单元模型单元模型构造单元模型构造单元模型构造方法单元模型构造方法单元模型构造方法单元模型构造方法收敛性条件
①在单元内，场函数必须是连续的；

②完备性：插值多项式的阶次必须由低到高依次增加，不能出现跳跃现象；

③协调性：各单元边界必须连续，单元边界不能出现开裂现象。插值多项式收敛性条件插值多项式收敛性条件插值多项式选择条件插值多项式选择条件插值多项式选择条件插值多项式选择条件单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元模型构造—整体坐标系法单元刚度矩阵—2节点线单元单元刚度矩阵—2节点线单元单元刚度矩阵—三角形单元单元刚度矩阵—三角形单元单元刚度矩阵—三角形单元单元刚度矩阵—三角形单元单元刚度矩阵—三角形单元作业单元模型构造—整体坐标系法单元模型—等参单元单元模型—等参单元单元模型—等参单元单元模型—等参单元单元平衡方程组装过程单元平衡方程组装过程单元平衡方程组装过程单元平衡方程组装过程单元平衡方程组装过程单元平衡方程组装过程单元平衡方程组装过程总体刚度矩阵K的特性约束处理过程约束处理过程—边界条件约束处理过程—模型简化约束处理过程—模型简化约束处理过程—约束方程约束处理过程—约束处理方法约束处理过程—赋0赋1法约束处理过程—赋0赋1法约束处理过程—赋0赋1法约束处理过程—赋0赋1法约束处理过程—赋0赋1法约束处理过程—赋0赋1法约束处理过程—赋0赋1法约束处理过程—乘大数法约束处理过程—乘大数法约束处理过程—乘大数法约束处理过程—乘大数法约束处理过程—乘大数法约束处理过程—两种方法比较约束处理过程—两种方法比较约束处理过程—两种方法比较约束处理过程—弹簧单元弹簧约束方程f=kU4方程组求解过程—特点方程组求解过程—分类比较方程组求解过程—带宽定义方程组求解过程—带宽方程组求解过程—带宽方程组求解过程—系数矩阵存贮方程组求解过程—二维等带宽存贮方程组求解过程—二维等带宽存贮方程组求解过程—一维变带宽存贮按行一维变带宽存贮一维变带宽存贮是最节省内存的一种方法，但是由于要借助于寻址数组寻找系数矩阵元素的位置，相对二维等带宽存贮方法来说要复杂一些，而且在程序实现时也要复杂得多，方程组求解过程中也要消耗一些数组寻址时间。因此，在选用存贮方法时要权衡二者的利弊，统盘考虑。一般当带宽变化不大，计算机内存允许时，采用二维等带宽存贮方法是比较合适的。方程组求解过程—求解方法应变、应力回代过程有限差分法从弹性力学的基本方程建立以来，这些方程在各种问题的边界条件下如何求解，一直是很多数学工作者和力学工作者研究的内容。即弹性力学的经典解法存在一定的局限性，当弹性体的边界条件和受载情况复杂一点，往往无法求得偏微分方程的边值问题的解析解，许多工程重要问题，不能够得出函数式的解答。

因此，弹性力学问题的各种数值解法便具有重要的实际意义。工程中常用的数值解法有有限单元法和差分法。第一节差分方程第一节差分方程我们在弹性体上，用相隔等间距h而平行于坐标轴的两组平行线织成正方形网格，Δx=Δy=h，如图。我们将只考虑离开结点０充分近的那些结点，即（x-x0）充分小。于是可不计（x-x0）的三次及更高次幂的各项，则上式简写为：联立(c),(d),解得差分公式：差分公式(１-１)及(１-３)是以相隔2h的两结点处的函数值来表示中间结点处的一阶导数值，可称为中点导数公式。以上(１-１)~(１-