
疲劳与断裂力学 第章 线弹性断裂力学基础.ppt

15****92





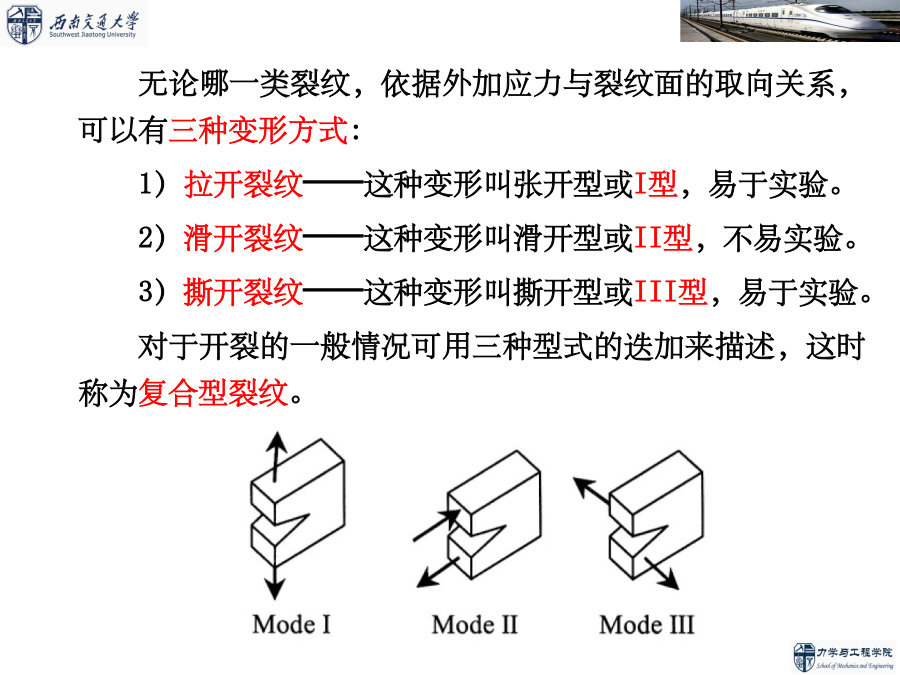



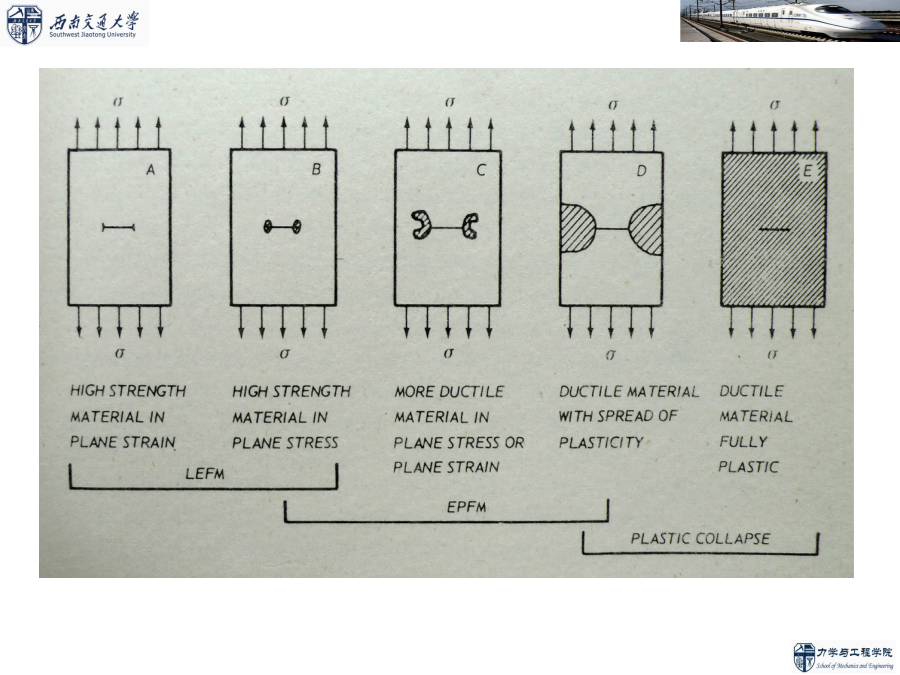
亲,该文档总共83页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

疲劳与断裂力学 第章 线弹性断裂力学基础.ppt
第五章线弹性断裂力学强度材料抵抗破坏的能力断裂力学和材料力学、弹塑性力学的相同点:都是宏观的强度理论,都研究材料的受力、变形和断裂。断裂力学和材料力学、弹塑性力学的不同点:材料力学、弹塑性力学的基本假设是材料均匀、连续;而断裂力学则假定材料内部存在着一条或几条裂纹。断裂力学就是裂纹体力学裂纹是断裂力学从实际材料中存在的各种缺陷(如气孔、夹杂、疏松、缩孔、白点、应力腐蚀引起的蚀坑、交变荷载下产生的疲劳源)中抽象出来的力学模型。断裂力学中定义的裂纹的最大特点是裂纹尖端曲率半径,这种裂纹又叫“尖裂纹”。断裂力学

疲劳与断裂力学 第4章 结构疲劳分析基础.ppt
第四章结构疲劳分析基础结构疲劳分析第一节基于应力的结构疲劳分析方法缺口对S-N曲线的影响q的取值介于0到1之间,即:缺口大小和应力梯度对Kf的影响材料极限强度对Kf的影响由缺口敏感系数q的定义式可得高、低强度钢的缺口敏感系数曲线对高强度钢(Su>560MPa)铝合金材料的aN和Su的关系曲线二、名义应力法名义应力法估算结构疲劳寿命的步骤:名义应力法估算构件疲劳寿命的两种做法:例题一:如图所示一变截面杆,D=39mm,d=30mm,r=3mm。材料为40CrNiMoA,强度极限sb=1100MPa,受到交变

基于线弹性断裂力学的铝合金疲劳寿命预测.docx
基于线弹性断裂力学的铝合金疲劳寿命预测摘要:本文基于线弹性断裂力学理论,针对铝合金材料在高应力下易发生疲劳断裂的问题,提出了寿命预测方法。首先,介绍了铝合金材料的组织结构和疲劳断裂的基本特点。然后,详细解释了线弹性断裂力学的基本概念及应用方法。接着,以铝合金材料的实验数据为基础,利用线弹性断裂力学模型对其疲劳寿命进行了预测。最后,分析了模型的适用范围和改进方向。该研究结果对于提高铝合金材料的疲劳寿命,提高工程设计的可靠性具有一定的参考价值。关键词:铝合金;疲劳寿命;线弹性断裂力学;寿命预测一、引言铝合金材

疲劳与断裂力学弹塑性断裂力学基础.pptx
会计学线弹性(tánxìng)断裂力学弹塑性断裂力学的任务:在大范围屈服下,确定能定量描述裂纹尖端区域弹塑性应力、应变场强度的参量。以便利用理论建立起这些参量与裂纹几何(jǐhé)特性、外加载荷之间的关系,通过试验来测定它们,并最后建立便于工程应用的断裂准则。一、COD二、小范围屈服(qūfú)条件下的CTOD准则Dugdale模型假设:裂纹尖端的塑性区沿裂纹尖端两端延伸(yánshēn)呈尖劈带状。塑性区的材料为理想塑性状态,整个裂纹和塑性区周围仍为广大的弹性区所包围。塑性区与弹性区交界面上作用有均匀分

线弹性断裂力学..word版本.ppt
线弹性断裂力学思考?思考?一、弹性应力场分析方法I型裂纹尖端附近的应力应变场I型裂纹尖端附近的应力应变场I型裂纹尖端附近的应力应变场I型裂纹尖端附近的应力应变场I型裂纹尖端附近的应力应变场裂纹尖端附近的应力应变场裂纹尖端附近的应力应变场裂纹尖端附近的应力应变场---典型的拉伸曲线裂纹尖端附近的应力应变场裂纹尖端附近的应力应变场-塑性区裂纹尖端附近的应力应变场二、应力强度因子方法应力强度因子-KI应力强度因子-KI应力强度因子-KI应力强度因子-KI裂纹尺寸一定,KI值随载荷应力s的增大而增大。当KI增大到
