疲劳与断裂力学 第4章 结构疲劳分析基础.ppt

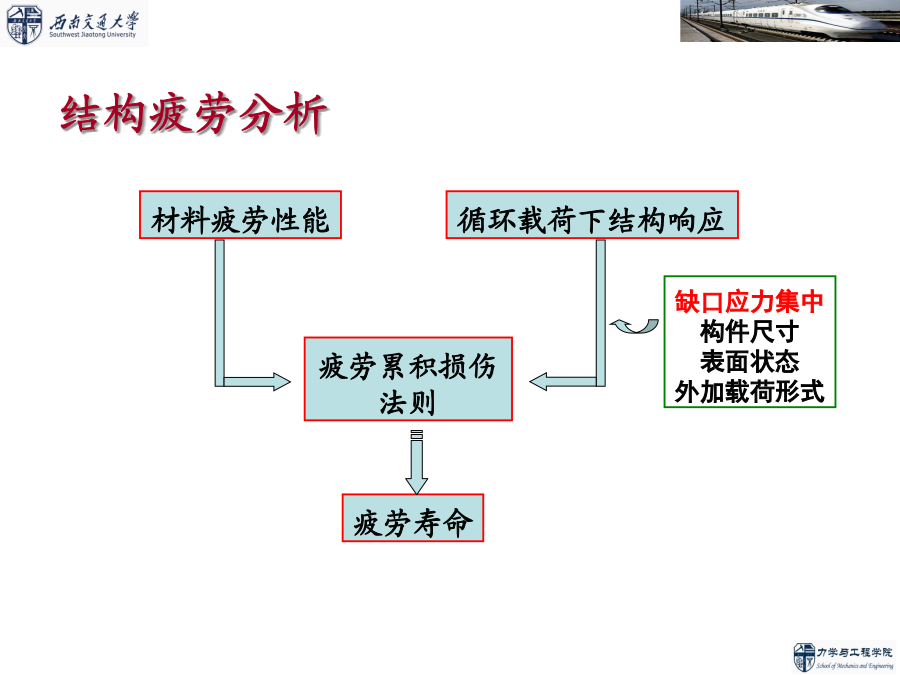
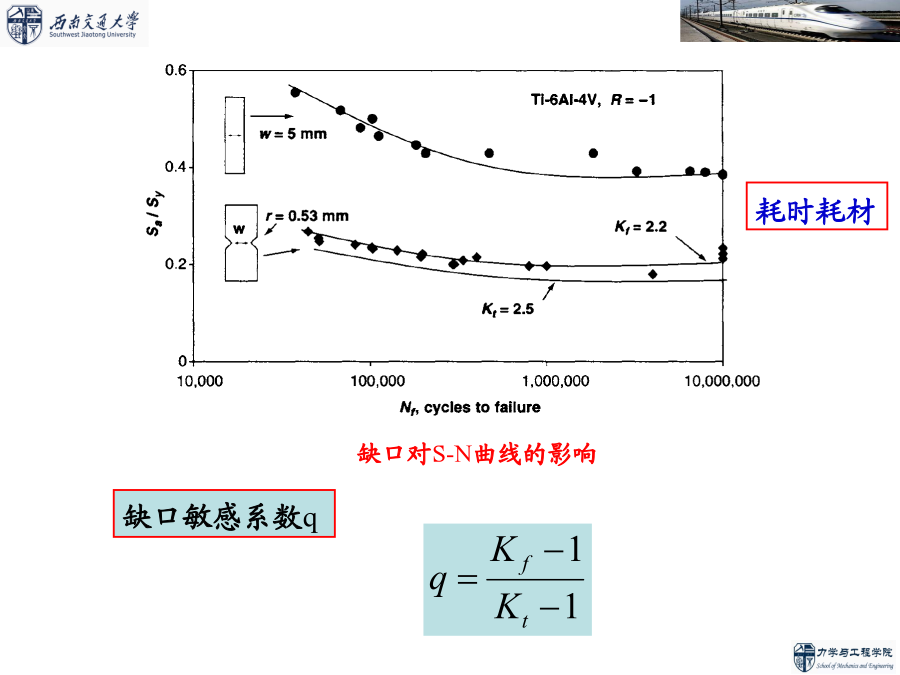
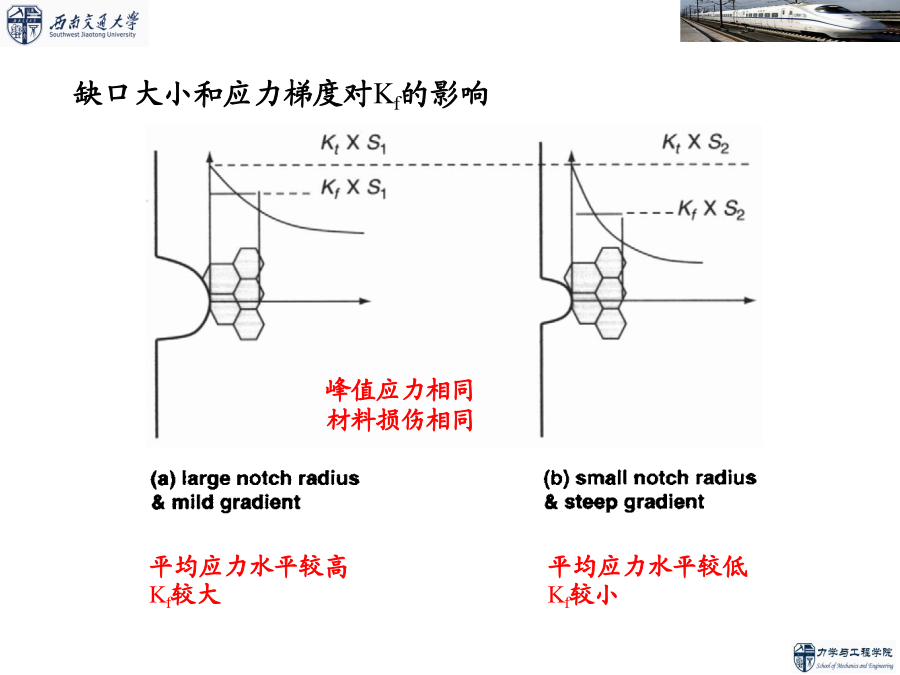
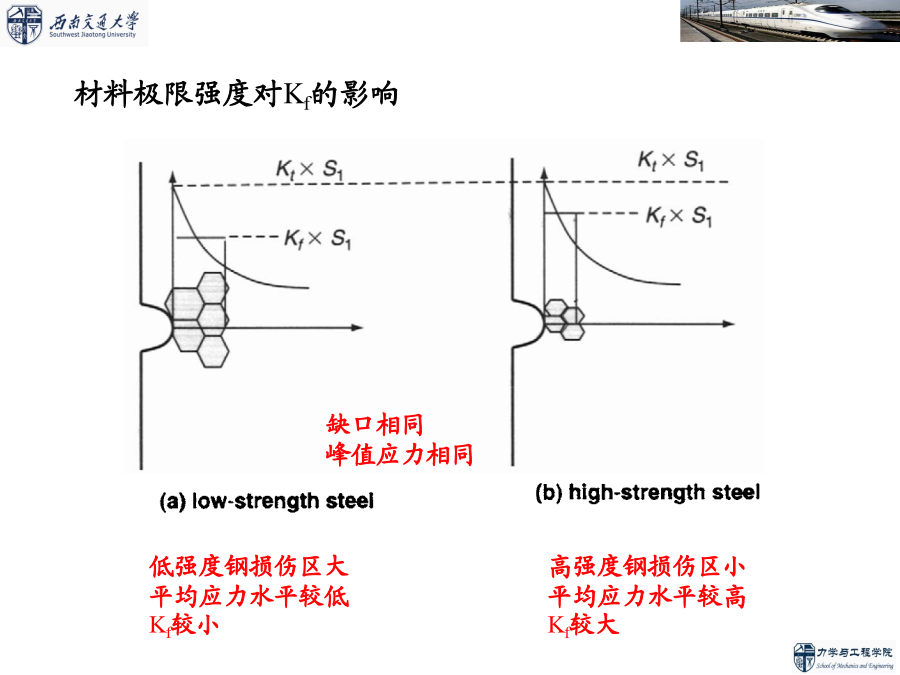
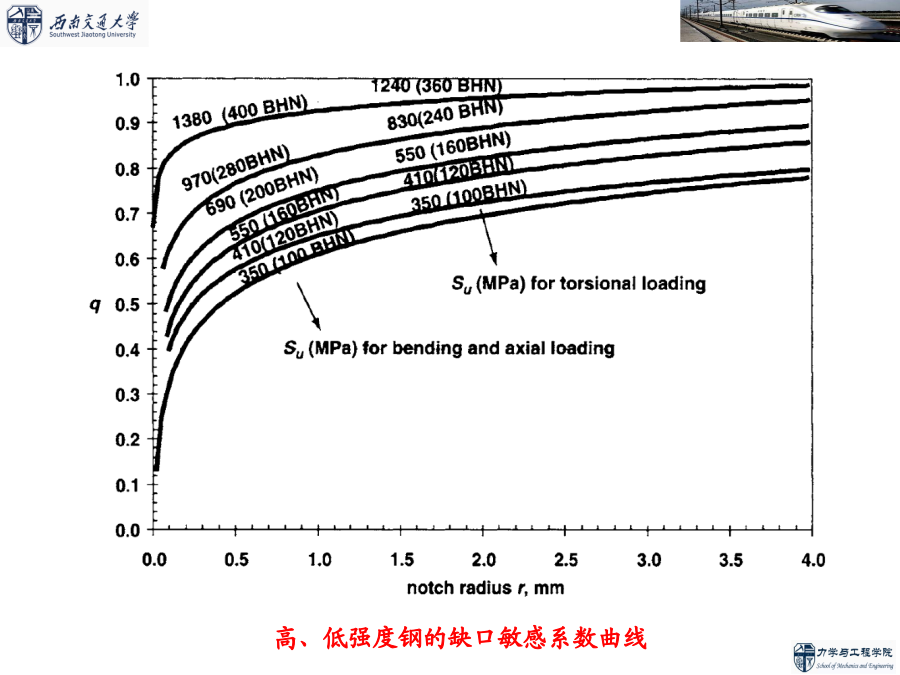
第四章结构疲劳分析基础结构疲劳分析第一节基于应力的结构疲劳分析方法缺口对S-N曲线的影响q的取值介于0到1之间，即：缺口大小和应力梯度对Kf的影响材料极限强度对Kf的影响由缺口敏感系数q的定义式可得高、低强度钢的缺口敏感系数曲线对高强度钢（Su>560MPa）铝合金材料的aN和Su的关系曲线二、名义应力法名义应力法估算结构疲劳寿命的步骤：名义应力法估算构件疲劳寿命的两种做法：例题一：如图所示一变截面杆，D=39mm，d=30mm，r=3mm。材料为40CrNiMoA，强度极限sb=1100MPa，受到交变载荷的作用，Pmax=400kN，Pmin=-100kN，试估算其疲劳寿命。（2）S-N曲线（3）理论应力集中系数Kt（4）拉杆的S-N曲线（5）疲劳寿命例题二：如图所示一含中心孔的LY12-CZ铝合金板，板宽W=50mm，孔直径D=8mm。名义应力谱见下表，试求其疲劳寿命。解：（1）S-N曲线（2）理论应力集中系数Kt（3）插值求出Kt=2.6时的S-N曲线（4）疲劳寿命估算最后，有Miner疲劳损伤累积理论可得：第二节基于应变的结构疲劳分析方法再由应力-应变关系
e=s/E+(s/K)1/n
计算局部应力s。
图中，Neuber双曲线与材料s-e曲线的交点D，就是Neuber理论的解答，比线性解答保守。1)线性理论
有:e=Kte=3×0.01=0.03
由应力-应变曲线：
e=0.03=s/60000+(s/2000)8
可解出:s=1138MPa可见，Neuber理论估计的s,e大于线性理论，是偏于保守的，工程中常用。二、局部应力应变法局部应力应力法估算结构疲劳寿命的步骤：3、所需材料性能数据5、缺口弹塑性应力应变的Neuber解和有限元解的比较首先计算缺口的理论应力集中系数Kt，有:
Kt=2.518结论：1）中等塑性范围内，两者十分接近；
2）弹性范围内，Neuber解小于有限元解；
3）大塑性时，Neuber解也小于有限元解。6、局部应力应变法的具体计算过程3)第i点对应的缺口局部si、ei为：
si+1=siDsi-i+1；
ei+1=eiDei-i+1
式中，加载时用“+”，卸载时用“-”。解：1)缺口应力-应变响应计算
0-1：S1=400MPa,计算e1,有:
e1=S1/E+(S1/K')1/n'=0.00202.Neuber双曲线：DsDe=Kt2DSDe=7.2
滞后环曲线：De=(Ds/E)+2(Ds/K')1/n'=7.2/Ds
解得：Ds1-2=1146；De1-2=0.006283。
故有：s2=820-1146=-326MPa,
2=0.0089-0.006283=0.002617
3)估算寿命，有：解：由Miner理论有:
ni/Ni=n1/N1+n2/N2=1
已知n1=5000。且由上例知：
在R=0,Smax1=400MPa下
寿命为：N1=12470,1)R=0.2,Smax2=500MPa时的缺口响应计算。2)画应力应变响应曲线。
由稳态环求出：
ea=0.003141,
sm=312MPa。