预览加载中，请您耐心等待几秒...

欧拉图和哈密尔顿图.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共17页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

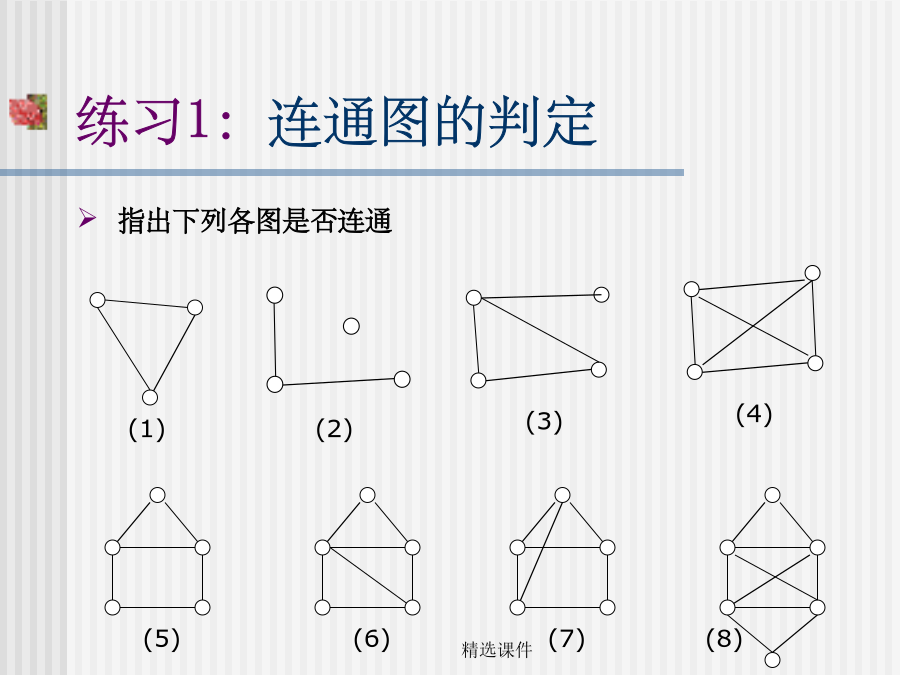
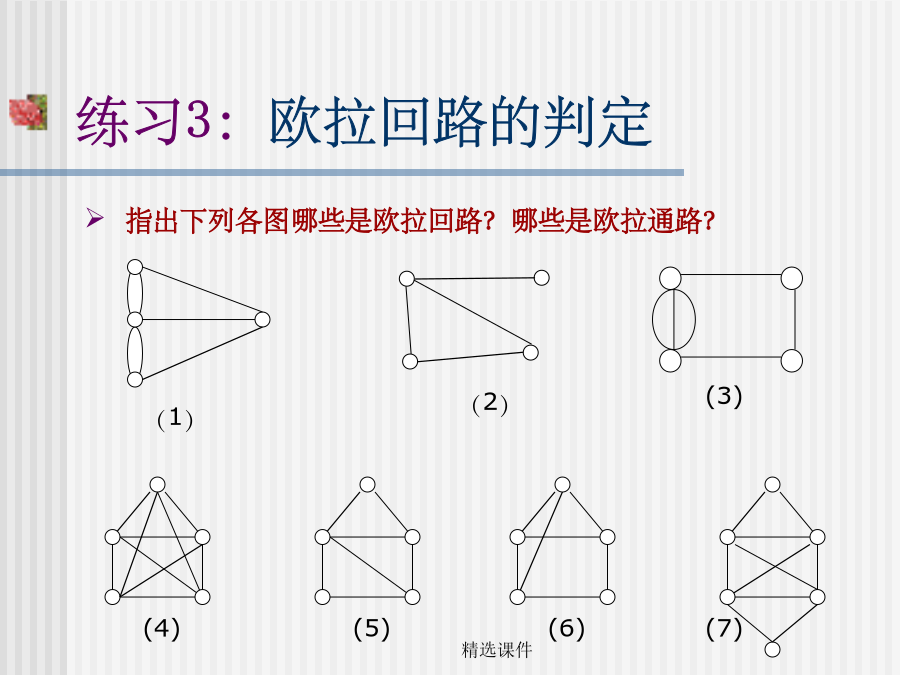
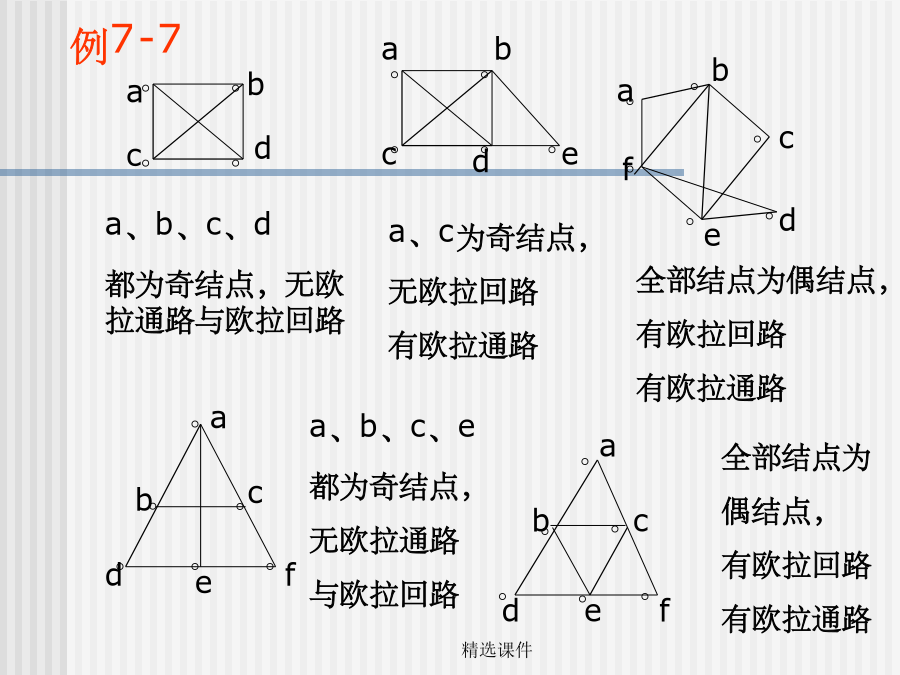
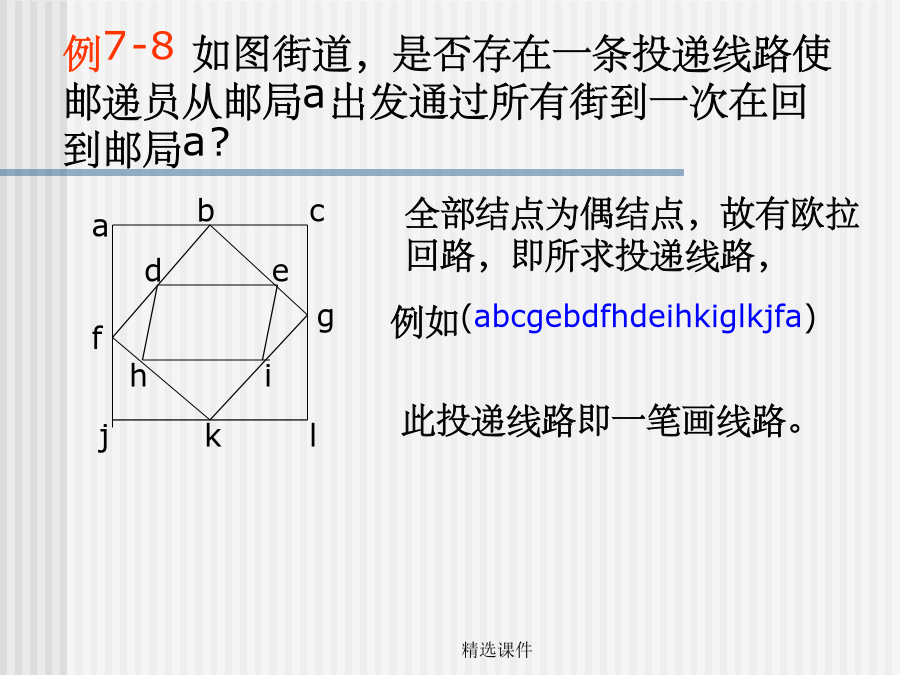
第二节图的连通性通路和回路无向图的连通性练习1：连通图的判定欧拉图定理7-4无向图G=<V，E>具有欧拉回路，即是欧拉图的充分必要条件是这个图是连通的，并且图G中所有结点的度数都是偶数，即都与偶数条边相连。练习3：欧拉回路的判定例7-7例7-8如图街道，是否存在一条投递线路使邮递员从邮局a出发通过所有街到一次在回到邮局a?一笔画问题：就是判断一个图形能否一笔画成,实质上就是判断图形是否存在欧拉通路和欧拉回路的问题。 练习3：一笔画的判定例7-9一笔画的判定哈密尔顿图1856年,英国数学家哈密尔顿设计了一个周游世界的游戏，他在一个正十二面体的二十个顶点上标上二十个著名城市的名字，要求游戏者从一个城市出发，经过每一个城市一次且仅一次，然后回到出发点。哈密尔顿回路图此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！