
期权定价公式及其应用.ppt

天马****23









亲,该文档总共44页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

期权定价公式及其应用.ppt
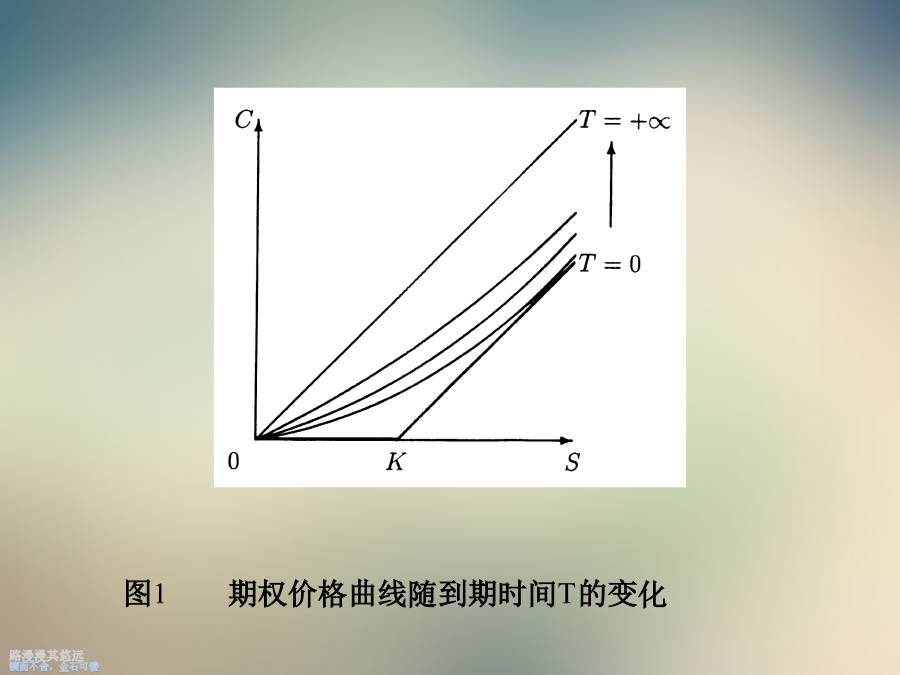
1.Black-Scholes公式经典的Black-Scholes期权定价公式是对于欧式股票期权给出的。其公式为K是期权的执行价格,r是无风险证券的(瞬时)收益率,称为股价的波动率{volatility,这是一个需要测算的参数}图1期权价格曲线随到期时间T的变化Black-Scholes公式的方便之处在于除股价的波动率外,其他参数都是直接在市场上可以找到的。例如,如果这里价格以元计,时间以年计,从而涉及的两个比率都指的是年率。那么(以下的等号实际上都是近似等号)把这些值代入公式,得到:2.金融资产的定价问

期权定价公式及其应用.ppt
2024/10/21图1期权价格曲线随到期时间T的变化把这些值代入公式,得到:2.金融资产的定价问题3.Black-Scholes公式发展过程是股票价格的平均增长率,(3)博内斯(Boness,1964)(4)塞缪尔森(Samuelson,1965)在1973年Black和Scholes提出Black—Scholes期权定价模型.20世纪60年代末,两人开始合作研究期权的定价问题,并找到了建立期权定价模型的关键突破点,即构造一个由标的股票和无风险债券的适当组合(买入适当数量的标的股票,同时按无风险利率借入

期权定价公式及其应用.ppt
1.Black-Scholes公式经典的Black-Scholes期权定价公式是对于欧式股票期权给出的。其公式为K是期权的执行价格,r是无风险证券的(瞬时)收益率,称为股价的波动率{volatility,这是一个需要测算的参数}图1期权价格曲线随到期时间T的变化Black-Scholes公式的方便之处在于除股价的波动率外,其他参数都是直接在市场上可以找到的。例如,如果这里价格以元计,时间以年计,从而涉及的两个比率都指的是年率。那么(以下的等号实际上都是近似等号)把这些值代入公式,得到:2.金融资产的定价问

期权定价公式及其应用.ppt
1.Black-Scholes公式经典的Black-Scholes期权定价公式是对于欧式股票期权给出的。其公式为K是期权的执行价格r是无风险证券的(瞬时)收益率称为股价的波动率{volatility这是一个需要测算的参数}图1期权价格曲线随到期时间T的变化Black-Scholes公式的方便之处在于除股价的波动率外其他参数都是直接在市场上可以找到的。例如如果这里价格以元计时间以年计从而涉及的两个比率

期权定价公式及其应用.ppt
1.Black-Scholes公式经典的Black-Scholes期权定价公式是对于欧式股票期权给出的。其公式为K是期权的执行价格r是无风险证券的(瞬时)收益率称为股价的波动率{volatility这是一个需要测算的参数}图1期权价格曲线随到期时间T的变化Black-Scholes公式的方便之处在于除股价的波动率外其他参数都是直接在市场上可以找到的。例如如果这里价格以元计时间以年计从而涉及的两个比率
