线性规划Matlab求解.ppt

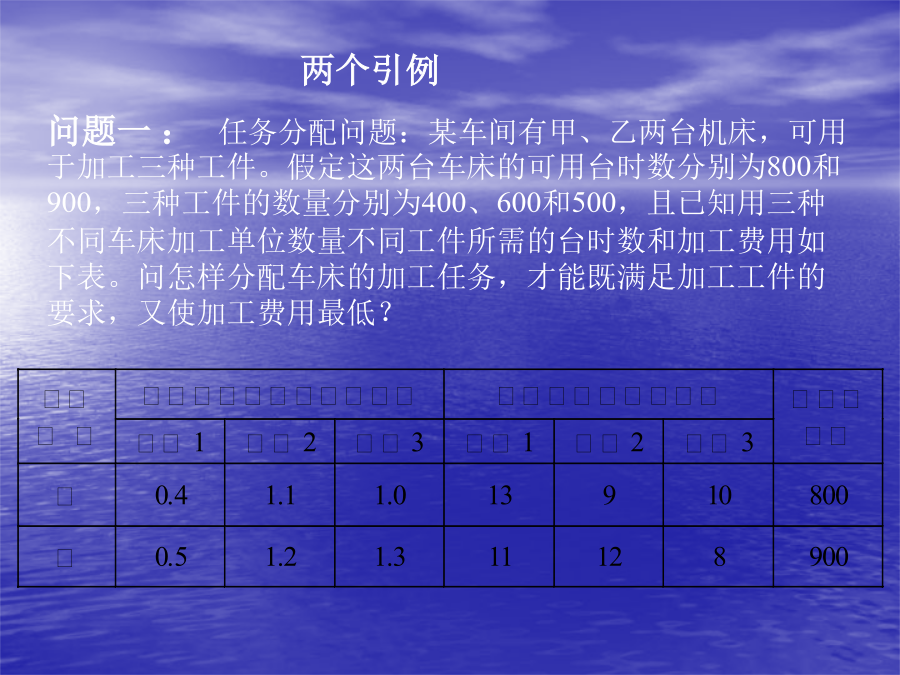
线性规划实验目的问题一：任务分配问题：某车间有甲、乙两台机床，可用于加工三种工件。假定这两台车床的可用台时数分别为800和900，三种工件的数量分别为400、600和500，且已知用三种不同车床加工单位数量不同工件所需的台时数和加工费用如下表。问怎样分配车床的加工任务，才能既满足加工工件的要求，又使加工费用最低？解设在甲车床上加工工件1、2、3的数量分别为x1、x2、x3，在乙车床上加工工件1、2、3的数量分别为x4、x5、x6。可建立以下线性规划模型：问题二：某厂每日8小时的产量不低于1800件。为了进行质量控制，计划聘请两种不同水平的检验员。一级检验员的标准为：速度25件/小时，正确率98%，计时工资4元/小时；二级检验员的标准为：速度15小时/件，正确率95%，计时工资3元/小时。检验员每错检一次，工厂要损失2元。为使总检验费用最省，该工厂应聘一级、二级检验员各几名？故目标函数为：线性规划模型：1.线性规划的标准形式：引入松弛变量x3,x4,x5,将不等式化为等式,即单纯形标准形:用MATLAB优化工具箱解线性规划3、模型：minz=cX

解编写M文件xxgh1.m如下：
c=[-0.4-0.28-0.32-0.72-0.64-0.6];
A=[0.010.010.010.030.030.03;0.02000.0500;00.02000.050;000.03000.08];
b=[850;700;100;900];
Aeq=[];beq=[];
vlb=[0;0;0;0;0;0];vub=[];
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)

S.t.编写M文件xxgh3.m如下:

f=[1391011128];
A=[0.41.11000
0000.51.21.3];
b=[800;900];
Aeq=[100100
010010
001001];
beq=[400600500];
vlb=zeros(6,1);
vub=[];
[x,fval]=linprog(f,A,b,Aeq,beq,vlb,vub)
结果:
x=
0.0000
600.0000
0.0000
400.0000
0.0000
500.0000
fval=1.3800e+004

即在甲机床上加工600个工件2,在乙机床上加工400个工件1、500个工件3，可在满足条件的情况下使总加工费最小为13800。编写M文件xxgh4.m如下：

c=[40;36];
A=[-5-3];
b=[-45];
Aeq=[];
beq=[];
vlb=zeros(2,1);
vub=[9;15];
%调用linprog函数：
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)

结果为：
x=
9.0000
0.0000
fval=360

即只需聘用9个一级检验员。
投资的收益和风险二、基本假设和符号规定三、模型的建立与分析四、模型1的求解a=0;
while(1.1-a)>1
c=[-0.05-0.27-0.19-0.185-0.185];
Aeq=[11.011.021.0451.065];beq=[1];
A=[00.025000;000.01500;0000.0550;00000.026];
b=[a;a;a;a];
vlb=[0,0,0,0,0];vub=[];
[x,val]=linprog(c,A,b,Aeq,beq,vlb,vub);
a
x=x'
Q=-val
plot(a,Q,'.')，axis([00.100.5])，holdon
a=a+0.001;
end
xlabel('a'),ylabel('Q')计算结果：五、结果分析实验作业