
数值分析报告上机题(matlab版)(东南大学).pdf

一吃****瀚文








亲,该文档总共22页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

数值分析报告上机题(matlab版)(东南大学).pdf
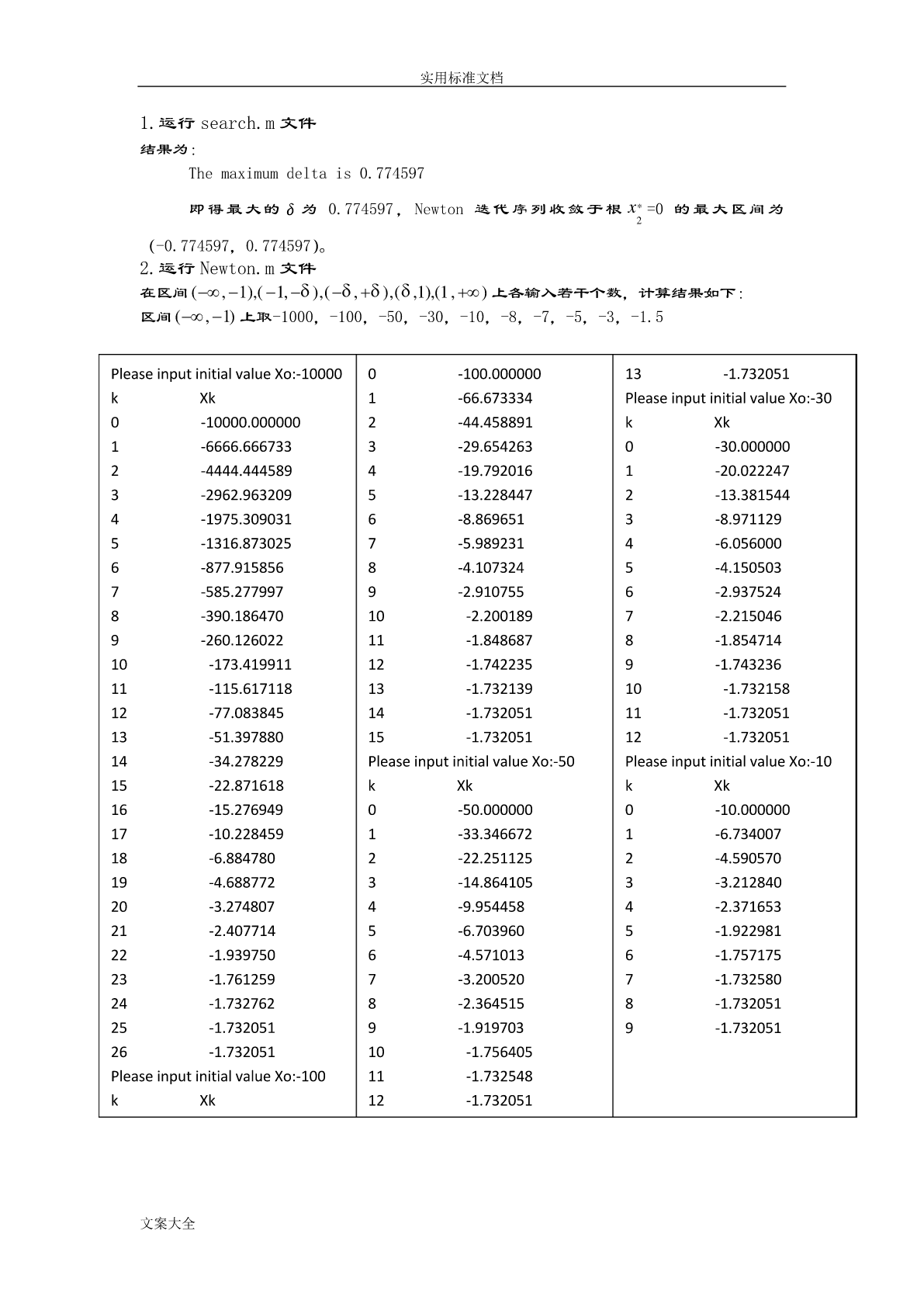
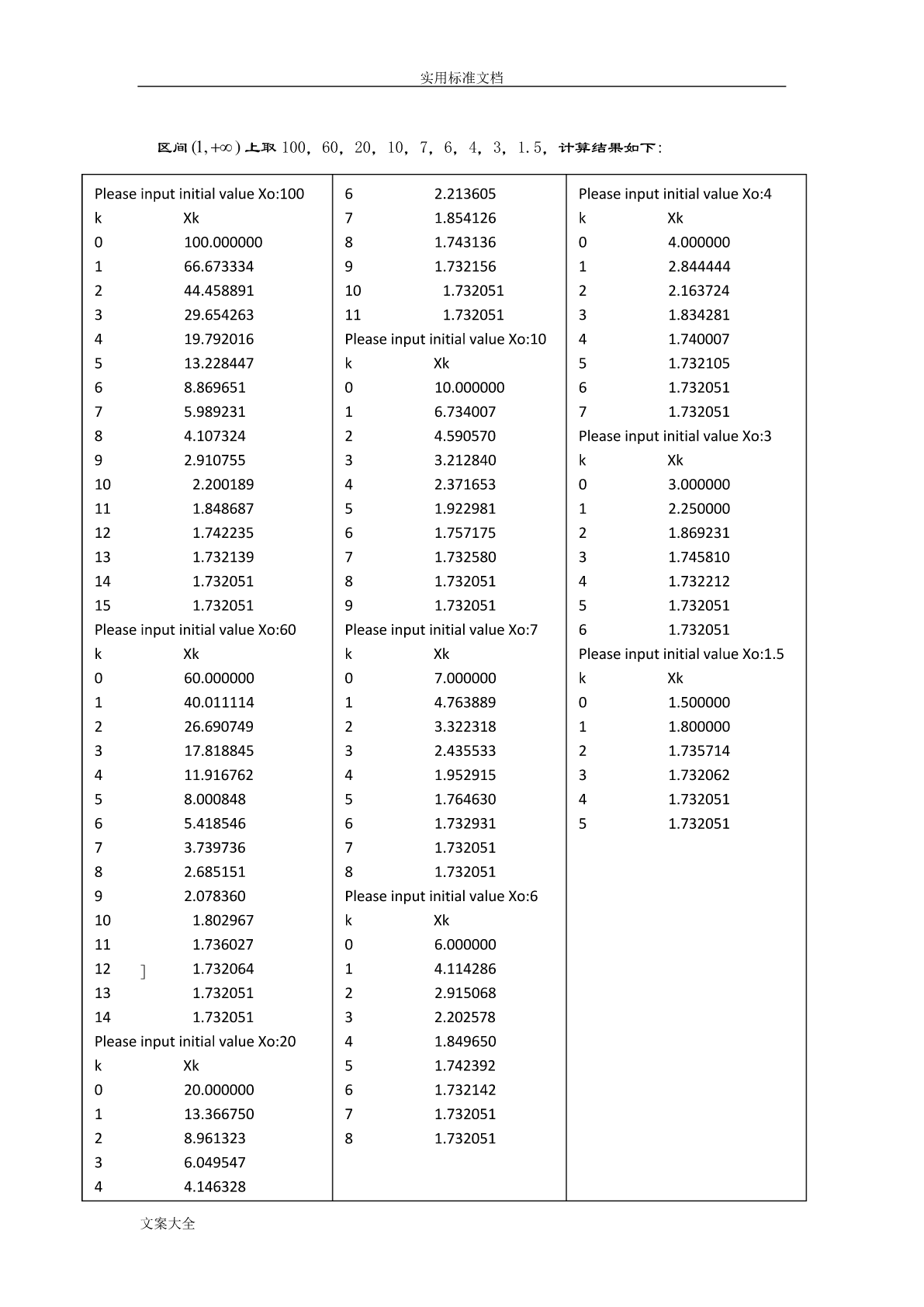
实用标准文档数值分析上机报告文案大全实用标准文档第一章一、题目1311精确值为()。22NN1111S1)编制按从大到小的顺序N,计算S的通用程序。221321N21N111S2)编制按从小到大的顺序N,计算S的通用N21(N1)21221N程序。SSS3)按两种顺序分别计算102,104,106,并指出有效位数。(编制程序时用单精度)4)通过本次上机题,你明白了什么?二、通用程序clearN=input('PleaseInputanN(N>1):');Accu

数值分析报告上机题(matlab版)(东南大学).pdf
实用标准文档数值分析上机报告文案大全实用标准文档第一章一、题目1311精确值为()。22NN11111)编制按从大到小的顺序SN,计算S的通用程序。221321N21N1112)编制按从小到大的顺序S,计算S的通用NNN21(N1)21221程序。3)按两种顺序分别计算S102,S104,S106,并指出有效位数。(编制程序时用单精度)4)通过本次上机题,你明白了什么?二、通用程序clearN=input('PleaseInputanN(N>1):');Accu

数值分析报告上机题(matlab版)(东南大学).pdf
实用标准文档数值分析上机报告文案大全实用标准文档第一章一、题目1311精确值为()。22NN11111)编制按从大到小的顺序SN,计算S的通用程序。221321N21N1112)编制按从小到大的顺序S,计算S的通用NNN21(N1)21221程序。3)按两种顺序分别计算S102,S104,S106,并指出有效位数。(编制程序时用单精度)4)通过本次上机题,你明白了什么?二、通用程序clearN=input('PleaseInputanN(N>1):');Accu

数值分析上机题(matlab版)(东南大学).doc
数值剖析上机讲演姓名:学号:专业:情况迷信与工程第一章一、标题精确值为。体例按从年夜到小的次序,盘算SN的通用次序。体例按从小到年夜的次序,盘算SN的通用次序。按两种次序分不盘算,并指出无效位数。〔体例次序时用单精度〕经过本次上机题,你清楚了什么?二、通用次序clearN=input('PleaseInputanN(N>1):');AccurateValue=single((0-1/(N+1)-1/N+3/2)/2);Sn1=single(0);fora=2:N;Sn1=Sn1+1/(a^2-1);end

数值分析上机题(matlab版)(东南大学).doc
数值剖析上机讲演姓名:学号:专业:情况迷信与工程第一章一、标题精确值为。体例按从年夜到小的次序,盘算SN的通用次序。体例按从小到年夜的次序,盘算SN的通用次序。按两种次序分不盘算,并指出无效位数。〔体例次序时用单精度〕经过本次上机题,你清楚了什么?二、通用次序clearN=input('PleaseInputanN(N>1):');AccurateValue=single((0-1/(N+1)-1/N+3/2)/2);Sn1=single(0);fora=2:N;Sn1=Sn1+1/(a^2-1);end
