
钢筋混凝土破坏准则及本构关系.ppt

sy****28


亲,该文档总共87页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
钢筋混凝土破坏准则及本构关系.pptx
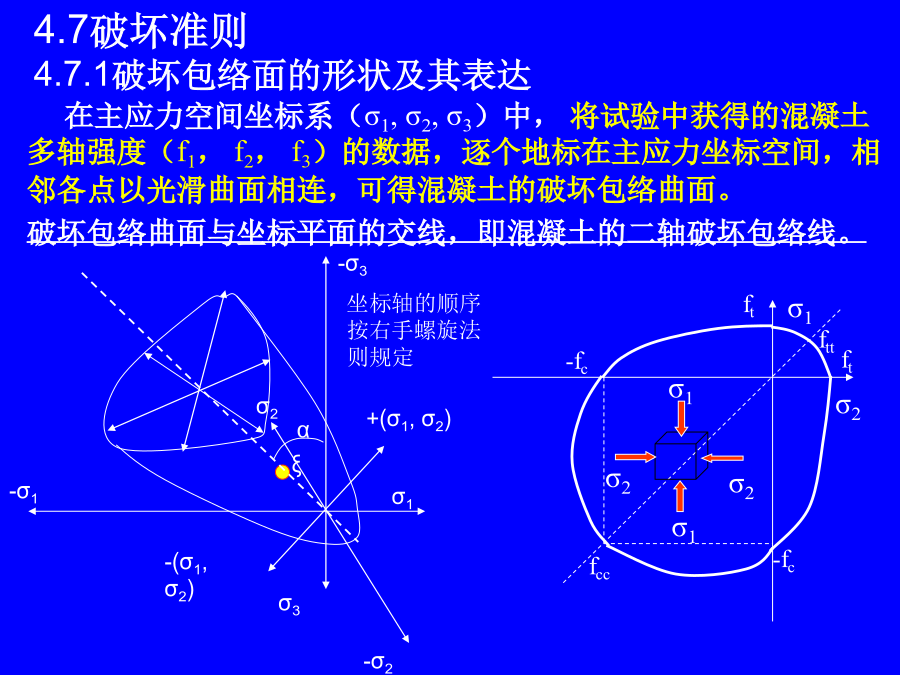
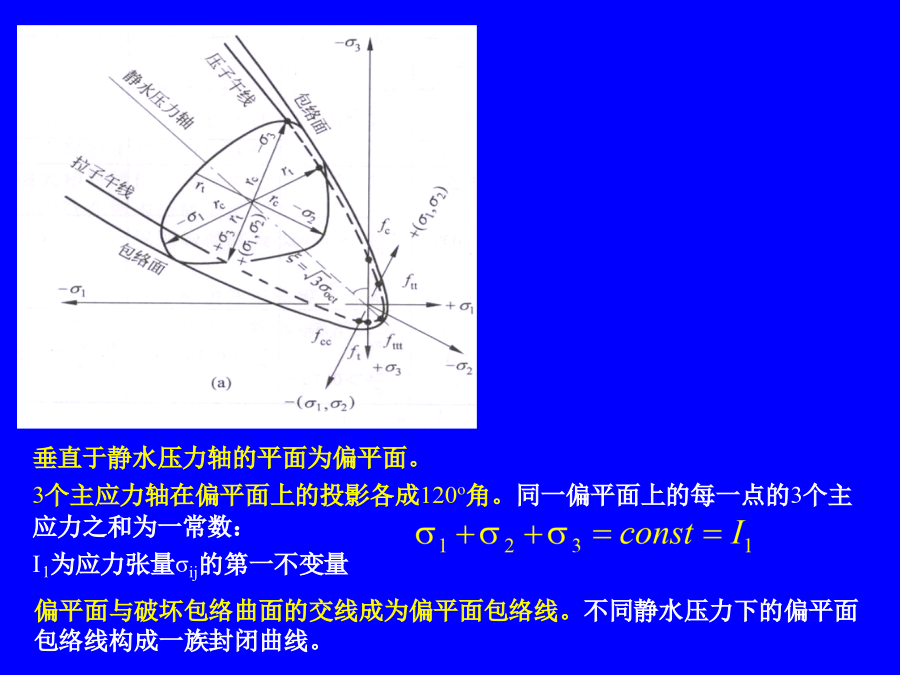
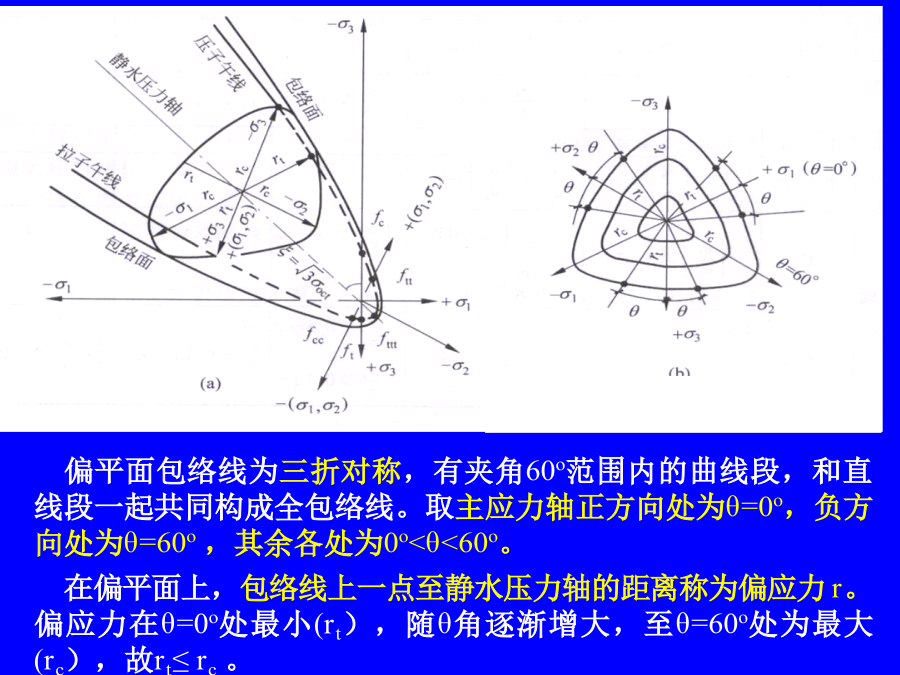
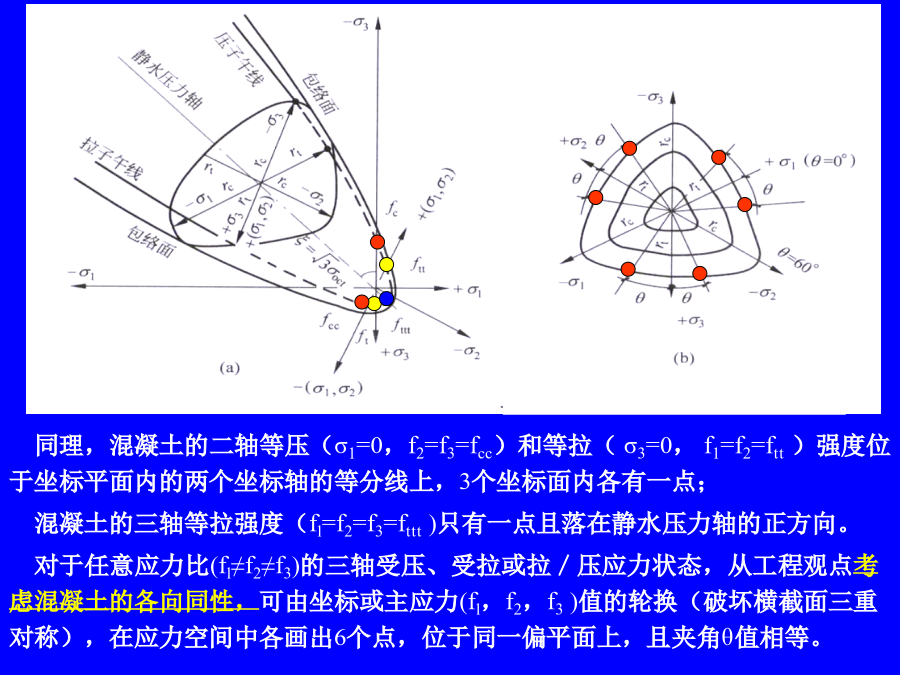
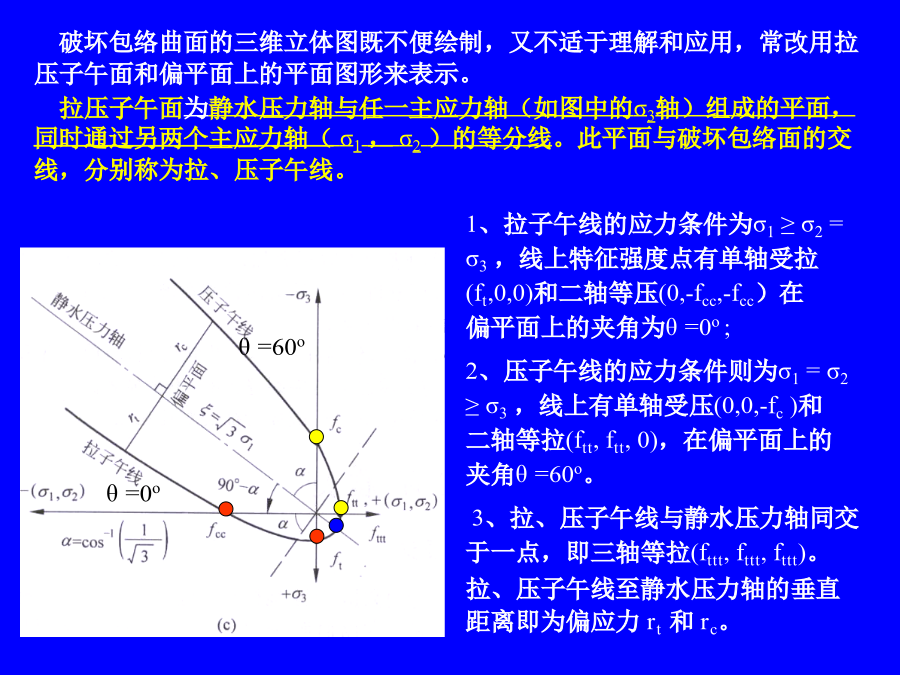
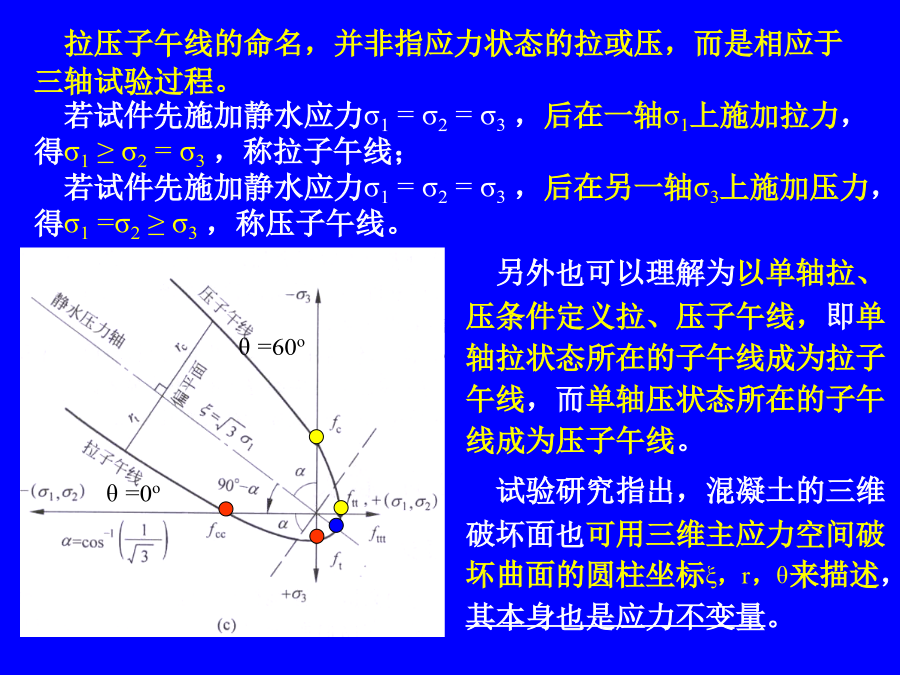
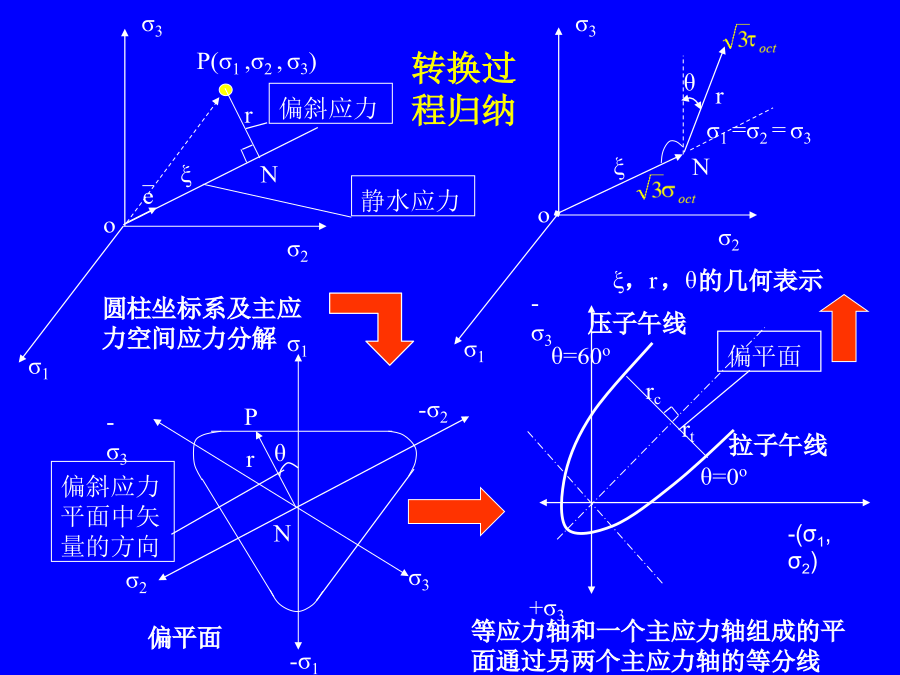
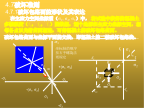
4.7破坏准则4.7.1破坏包络面的形状及其表达序言在主应力空间中,与各坐标轴保持等距的各点连结成为静水压力轴(即各点应力状态均满足:σ1=σ2=σ3)。此轴必通过坐标原点,且与各坐标轴的夹角相等,均为垂直于静水压力轴的平面为偏平面。3个主应力轴在偏平面上的投影各成120o角。同一偏平面上的每一点的3个主应力之和为一常数:I1为应力张量σij的第一不变量偏平面包络线为三折对称,有夹角60o范围内的曲线段,和直线段一起共同构成全包络线。取主应力轴正方向处为θ=0o,负方向处为θ=60o,其余各处为0o<θ<

钢筋混凝土破坏准则及本构关系.ppt
4.7破坏准则4.7.1破坏包络面的形状及其表达在主应力空间中,与各坐标轴保持等距的各点连结成为静水压力轴(即各点应力状态均满足:σ1=σ2=σ3)。此轴必通过坐标原点,且与各坐标轴的夹角相等,均为垂直于静水压力轴的平面为偏平面。3个主应力轴在偏平面上的投影各成120o角。同一偏平面上的每一点的3个主应力之和为一常数:I1为应力张量σij的第一不变量偏平面包络线为三折对称,有夹角60o范围内的曲线段,和直线段一起共同构成全包络线。取主应力轴正方向处为θ=0o,负方向处为θ=60o,其余各处为0o<θ<60

钢筋混凝土破坏准则及本构关系学习.pptx
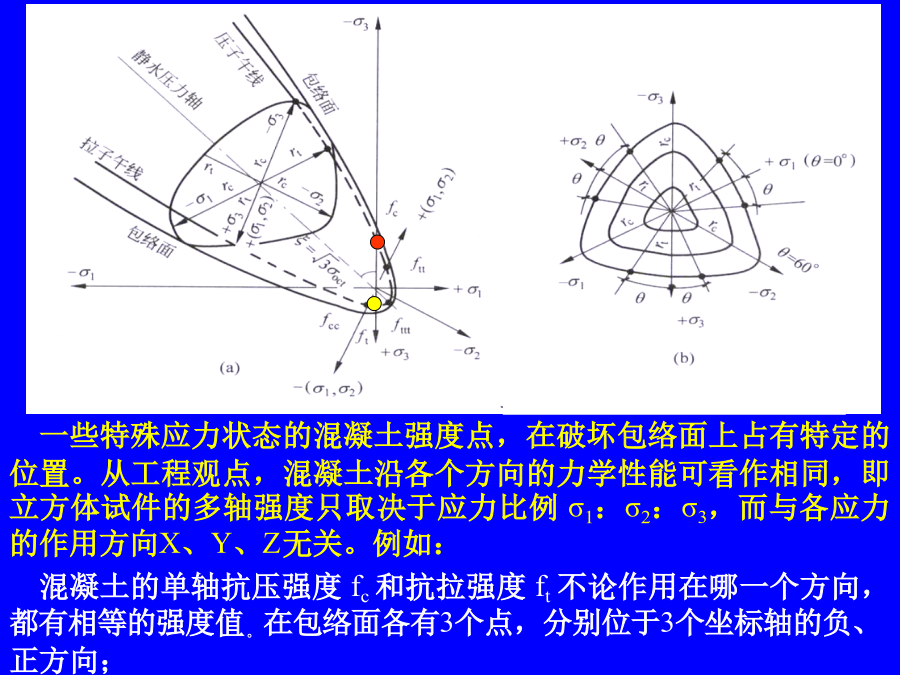
会计学在主应力空间中,与各坐标轴保持等距的各点连结成为静水压力轴(即各点应力状态均满足:σ1=σ2=σ3)。此轴必通过坐标原点,且与各坐标轴的夹角相等,均为垂直于静水压力轴的平面为偏平面。3个主应力轴在偏平面上的投影各成120o角。同一偏平面上的每一点的3个主应力之和为一常数:I1为应力张量σij的第一不变量偏平面包络线为三折对称,有夹角60o范围内的曲线段,和直线段一起共同构成全包络线。取主应力轴正方向处为θ=0o,负方向处为θ=60o,其余各处为0o<θ<60o。在偏平面上,包络线上一点至静水压力轴的

塑性混凝土受压本构关系模型与破坏准则的任务书.docx
塑性混凝土受压本构关系模型与破坏准则的任务书任务书:塑性混凝土受压本构关系模型与破坏准则一、背景介绍塑性混凝土广泛应用于结构工程中的桥梁、隧道、高层建筑等项目中。在强度设计和分析过程中,塑性混凝土的受压性能与破坏准则是十分关键的因素。因此,本任务旨在探究塑性混凝土受压本构关系模型及破坏准则,以期提高结构工程建模的精度和可靠性。二、任务内容1.塑性混凝土受压本构关系模型的研究。如何建立塑性混凝土的受压本构关系模型,是本任务的核心问题。任务要求综合考虑材料基本力学性质、试验数据及一般受的荷载特点,分析各种参数

附录C钢筋混凝土本构关系与混凝土多轴强度准则.doc
(完整word版)附录C:钢筋、混凝土本构关系与混凝土多轴强度准则(完整word版)附录C:钢筋、混凝土本构关系与混凝土多轴强度准则(完整word版)附录C:钢筋、混凝土本构关系与混凝土多轴强度准则附录C钢筋、混凝土本构关系与混凝土多轴强度准则C。1钢筋本构关系C。1。1普通钢筋的屈服强度及极限强度的平均值fym、fstm可按下列公式计算:(C.1。1-1)(C。1.1-2)式中:fyk、fym——钢筋屈服强度的标准值、平均值;fstk、fstm——钢筋极限强度的标准值、平均值;δs—-钢筋强度的变异系数
