
[复变函数与积分变换][课件][第1章][复数与复变函数].pdf

qw****27



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

复变函数与积分变换复数与复变函数.pptx
会计学在一些理论和实际问题中,有许多几何量与物理量,如果用复数作为变量去刻画,则在研究过程中比较方便,在18世纪,数学家J.D’Alembert与L.Euler等人逐步阐明了复数的几何意义和物理意义,并应用复数和复变函数研究了流体力学等方面的一些问题.在本章中,首先介绍复数的有关知识,然后再引入复平面点集、复变函数以及复变函数的极限与连续等概念.1.1复数1.1.1复数域形如的数称为复数,其中x和y是任意的实数,分别称为复数z的实部与虚部,记作x=Rez,y=lmz;而i(也可记为)称为纯虚数单位.当Im

[复变函数与积分变换][课件][第1章][复数与复变函数].pdf
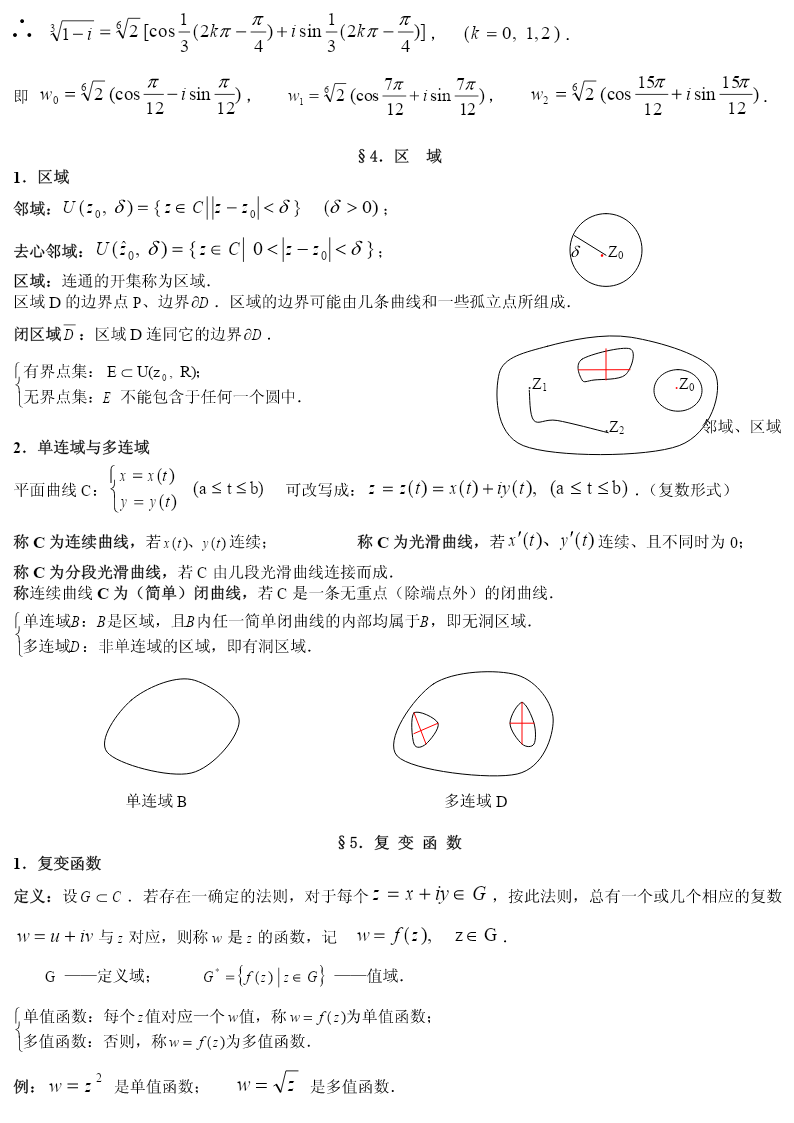
《复变函数》第一章复数与复变函数§1.复数及其代数运算复数:z=x+iy,i=−1——虚数单位.x=Re(z)——实部,y=Im(z)——虚部.两复数相等是指实部、虚部分别相等.复数间不能比较大小.复数的代数运算:z1=x1+iy1,z2=x2+iy2.加法:z1+z2=(x1+x2)+i(y1+y2);减法:z1−z2=(x1−x2)+i(y1−y2);zzzxx+yyxy−xy1=12=1212+i2112,(z≠0)乘法:z1⋅z2=(x1x2−y1y2)+i(x2y1+x1y2);除法:22222

经典复变函数与积分变换复数.ppt
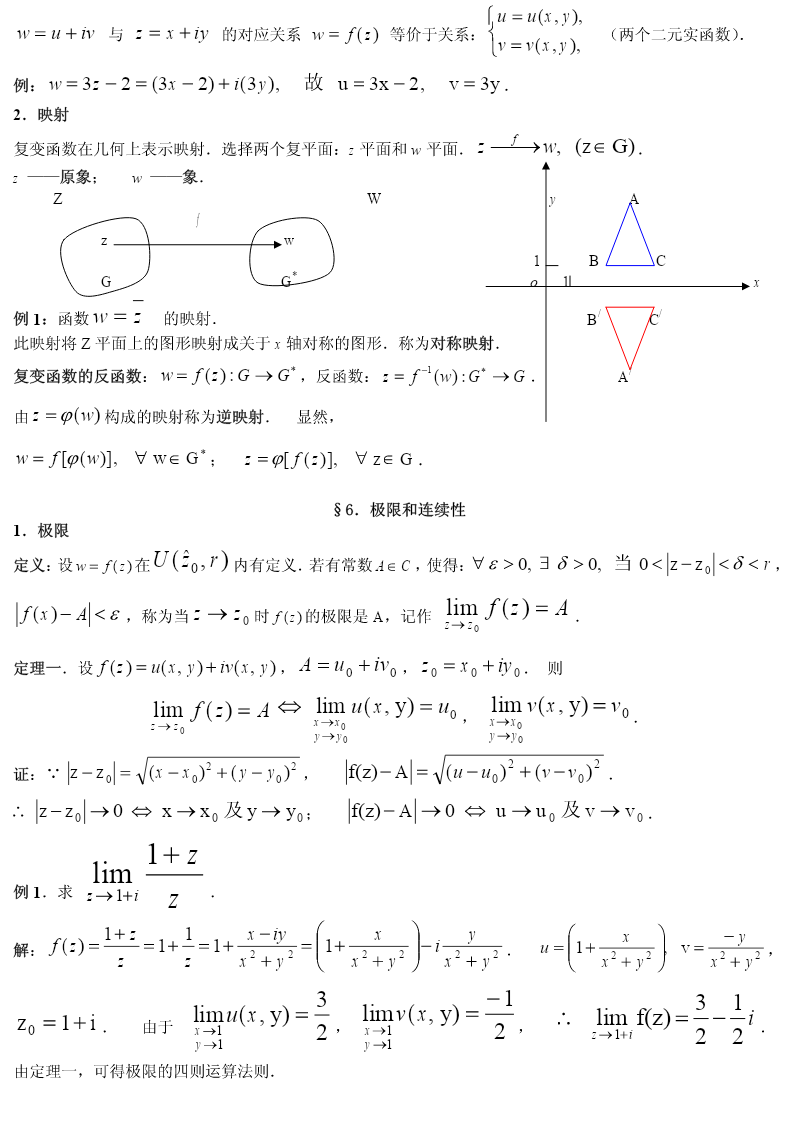
第一章复数与复变函数复变函数与积分变换及应用背景的概念,从而建立了复变函数理论.(4)应用于计算绕流问题中的压力和力矩等.变换应用于频谱分析和信号处理等.变换应用于控制问题.主要内容§1.1-1.2复数及其表示式1.1.1复数的概念显然,z=x+iy是x-yi的共轭复数,即1.1.2复数的四则运算(2)复数的积2.结合律解例1.2例1.3设z1,z2是两个复数,证明给定一复数z=x+yi,在坐标平面XOY上存在惟一的点P(x,y)与z=x+yi对应.反之,对XOY平面上的点P(x,y),存在惟一的复数z=

复变函数与积分变换—复变函数小结与习题.pptx
会计学一、重点与难点复数项级数1.复数列表达式2)复级数的收敛与发散非绝对收敛的收敛级数称为条件收敛级数.称为这级数的部分和.4.幂级数----阿贝尔Abel定理(3)既存在使级数发散的正实数,也存在使级数收在收敛圆周上是收敛还是发散,不能作出方法1:比值法5)幂级数的运算与性质如果当(2)5.泰勒级数2)常见函数的泰勒展开式6.洛朗级数函数根据正、负幂项组成的的级数的唯一性,可三、典型例题三、典型例题解解例2求下列幂级数的收敛半径/例3展开函数成的幂级数到项.分析:采用间接法即利用已知的展开式来求.由于

复变函数与积分变换课件.pptx
会计学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学
