
流体动力学(动量方程及伯努利方程一).ppt

天马****23







亲,该文档总共21页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

流体动力学(动量方程及伯努利方程一).ppt
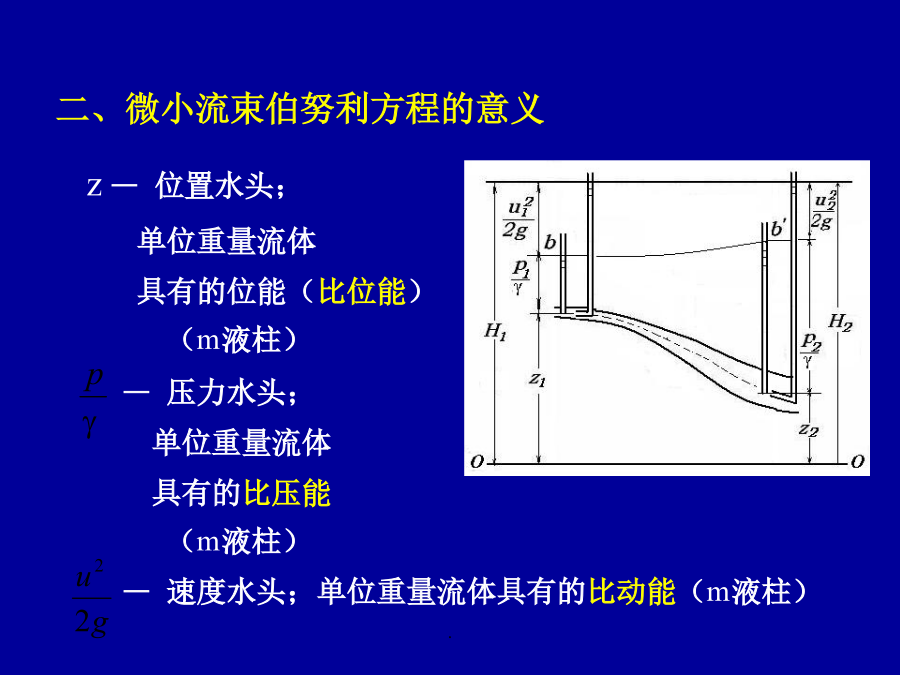
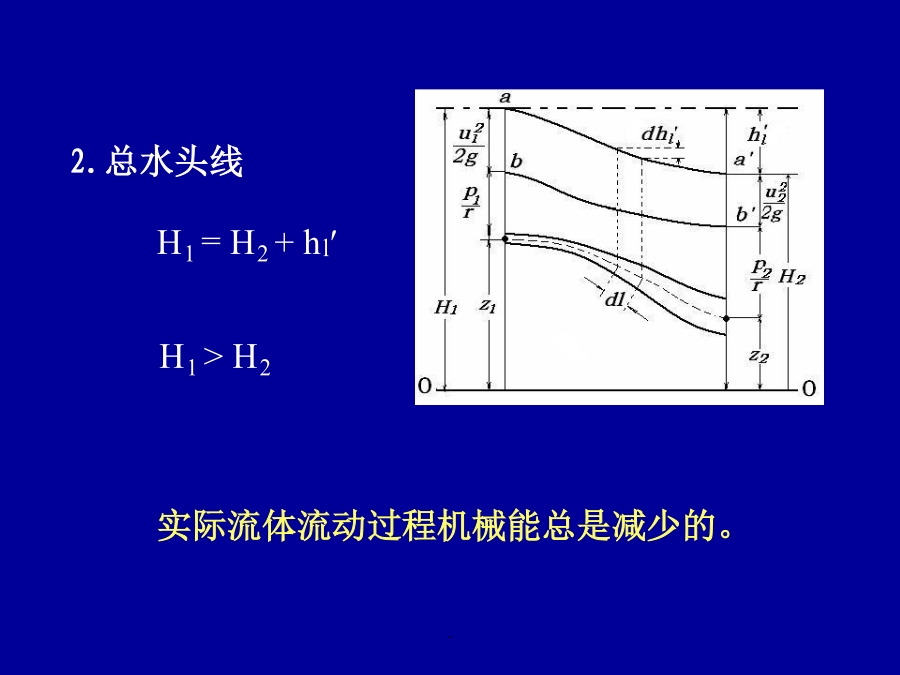
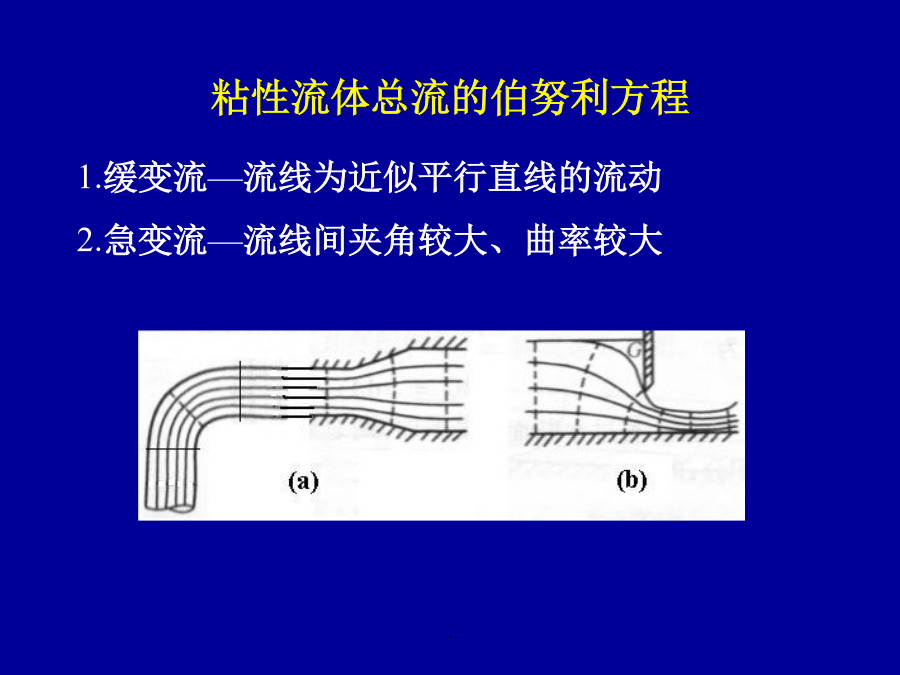
§5.5理想流体运动微分方程的伯努利积分得到下式由积分条件2.沿流线(即沿迹线)积分由积分条件3.仅在重力场中方程表示流线上各点u,p,z三者间关系;方程可以推广到微小流束。z—位置水头;单位重量流体具有的位能(比位能)(m液柱)—压力水头;单位重量流体具有的比压能(m液柱)—速度水头;单位重量流体具有的比动能(m液柱)—测压管水头;单位重量流体具有的比势能H—总水头;单位重量流体的总机械能,总比能粘性流体微小流束的伯努利方程2.总水头线H1=H2+hl′H1>H21.缓变流—流线为近似平行直线的流动2.

流体动力学(动量方程及伯努利方程一)-流体力学.ppt
§5.5理想流体运动微分方程的伯努利积分得到下式由积分条件2.沿流线(即沿迹线)积分由积分条件3.仅在重力场中方程表示流线上各点u,p,z三者间关系;方程可以推广到微小流束。z—位置水头;单位重量流体具有的位能(比位能)(m液柱)—压力水头;单位重量流体具有的比压能(m液柱)—速度水头;单位重量流体具有的比动能(m液柱)—测压管水头;单位重量流体具有的比势能H—总水头;单位重量流体的总机械能,总比能粘性流体微小流束的伯努利方程2.总水头线H1=H2+hl′H1>H21.缓变流—流线为近似平行直线的流动2.

第五章流体动力学(动量方程及伯努利方程一).ppt
§5.5理想流体运动微分方程的伯努利积分得到下式由积分条件2.沿流线(即沿迹线)积分由积分条件3.仅在重力场中方程表示流线上各点u,p,z三者间关系;方程可以推广到微小流束。z—位置水头;单位重量流体具有的位能(比位能)(m液柱)—压力水头;单位重量流体具有的比压能(m液柱)—速度水头;单位重量流体具有的比动能(m液柱)—测压管水头;单位重量流体具有的比势能H—总水头;单位重量流体的总机械能,总比能粘性流体微小流束的伯努利方程2.总水头线H1=H2+hl′H1>H21.缓变流—流线为近似平行直线的流动2.

流体动力学动量方程及伯努利方程一流体力学ppt课件.ppt
§5.5理想流体运动微分方程的伯努利积分得到下式由积分条件2.沿流线(即沿迹线)积分由积分条件3.仅在重力场中方程表示流线上各点u,p,z三者间关系;方程可以推广到微小流束。z—位置水头;单位重量流体具有的位能(比位能)(m液柱)—压力水头;单位重量流体具有的比压能(m液柱)—速度水头;单位重量流体具有的比动能(m液柱)—测压管水头;单位重量流体具有的比势能H—总水头;单位重量流体的总机械能,总比能粘性流体微小流束的伯努利方程2.总水头线H1=H2+hl′H1>H21.缓变流—流线为近似平行直线的流动2.

实验一 伯努利方程.docx
伯努利方程演示实验一、实验目的1掌握流体流动中各种能量或压头的定义及其相互转化关系,加深对伯努利方程式的理解。2观察静压头、位压头、动压头相互转换的规律。二、基本原理不可压缩流体在管内作稳定流动时,由于管路条件的变化,会引起流动过程中三种机械能(位能、动能、静压能)的相应改变及相互转换。对理想流体在系统内任一截面处,虽然三种能量不一定相等,但能量之和是守恒的。2.对于实际流体,由于存在内摩擦,流体在流东时总有一部分机械能损耗。3.以上机械能均可用测压管中的液柱高度表示。当测压孔正对流体流动方向时测压管中的
