
运筹学对偶问题ppt课件.ppt

天马****23








亲,该文档总共62页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

运筹学对偶问题ppt课件.ppt
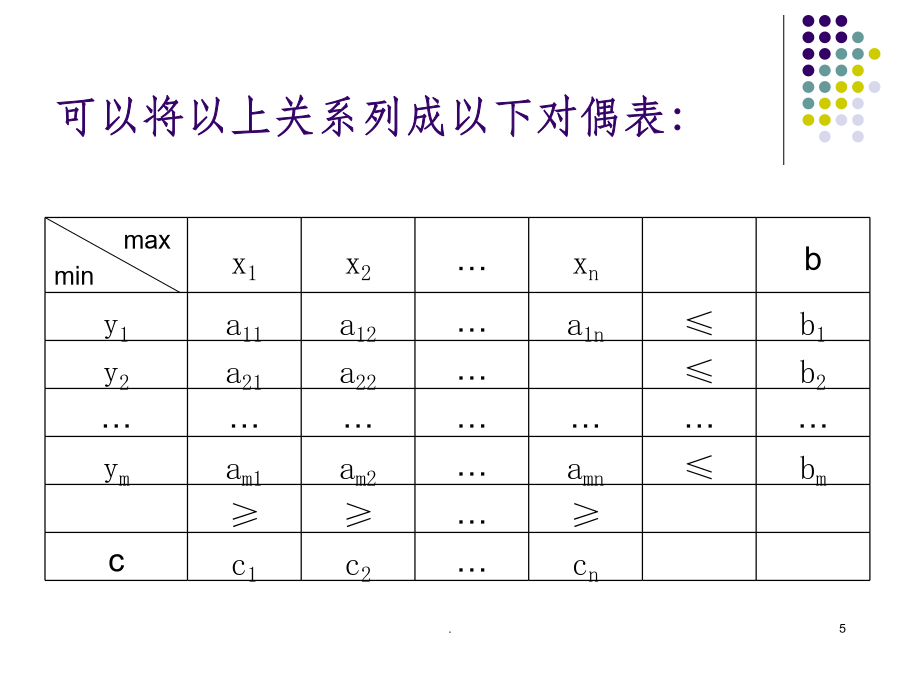
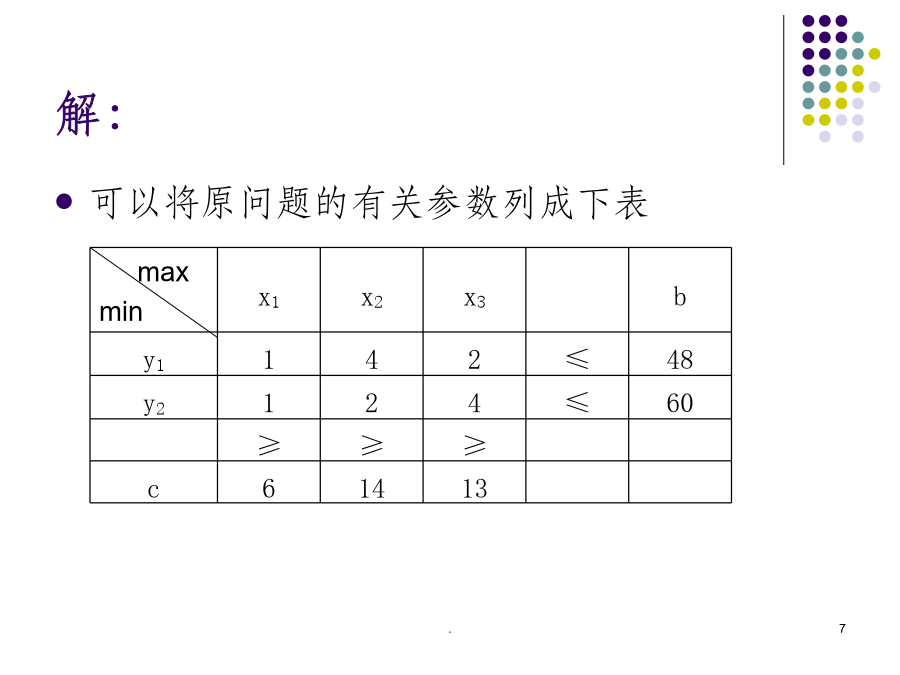
第四章对偶问题一、对偶问题的一般形式则以下线性规划问题:如果采用向量、矩阵来表示可以将以上关系列成以下对偶表:例解:∴对偶规划问题为比较两个条件:例对称化则,原问题变为则(A’)的对偶问题如下:对比结果调整令y1=y1’,y2=-y2’,y3=y4’-y3’则得到以下对偶问题合并比较原问题与对偶问题的相应关系例:写出下列问题的对偶形式:解:例:写出下列问题的对偶问题解:二、对偶问题的经济意义:例:某产品计划问题的线性规划数学模型为分析分析分析这样,就得到另一个线性规划模型:比较第二节对偶理论定理1(对称性
运筹学对偶理论ppt课件.ppt
第3章线性规划对偶理论及其应用线性规划的对偶模型对偶性质对偶问题的经济解释-影子价格对偶单纯形法线性规划的对偶模型线性规划的对偶模型线性规划的对偶模型线性规划的对偶模型线性规划的对偶模型线性规划的对偶模型线性规划的对偶模型线性规划的对偶模型线性规划的对偶模型线性规划的对偶模型线性规划的对偶模型资源定价问题(LP2)规范形式的线性规划问题规范形式的对偶关系非规范形式线性规划的对偶问题非规范形式线性规划的对偶问题总结课堂作业:求解下面线性规划的对偶规划对偶性质对偶性质对偶性质对偶性质对偶性质对偶性质对偶性质约

运筹学对偶问题.ppt
第四章对偶问题一、对偶问题的一般形式则以下线性规划问题:如果采用向量、矩阵来表示可以将以上关系列成以下对偶表:例解:∴对偶规划问题为比较两个条件:例对称化则,原问题变为则(A’)的对偶问题如下:对比结果调整令y1=y1’,y2=-y2’,y3=y4’-y3’则得到以下对偶问题合并比较原问题与对偶问题的相应关系例:写出下列问题的对偶形式:解:例:写出下列问题的对偶问题解:二、对偶问题的经济意义:例:某产品计划问题的线性规划数学模型为分析分析分析这样,就得到另一个线性规划模型:比较第二节对偶理论定理1(对称性

运筹学对偶问题.ppt
第四章对偶问题一、对偶问题的一般形式则以下线性规划问题:如果采用向量、矩阵来表示可以将以上关系列成以下对偶表:例解:∴对偶规划问题为比较两个条件:例对称化则,原问题变为则(A’)的对偶问题如下:对比结果调整令y1=y1’,y2=-y2’,y3=y4’-y3’则得到以下对偶问题合并比较原问题与对偶问题的相应关系例:写出下列问题的对偶形式:解:例:写出下列问题的对偶问题解:二、对偶问题的经济意义:例:某产品计划问题的线性规划数学模型为分析分析分析这样,就得到另一个线性规划模型:比较第二节对偶理论定理1(对称性

《运筹学对偶问题》.ppt
..............................................................
