非线性物理3-1(倍周期分岔到混沌、阵发性混沌).ppt

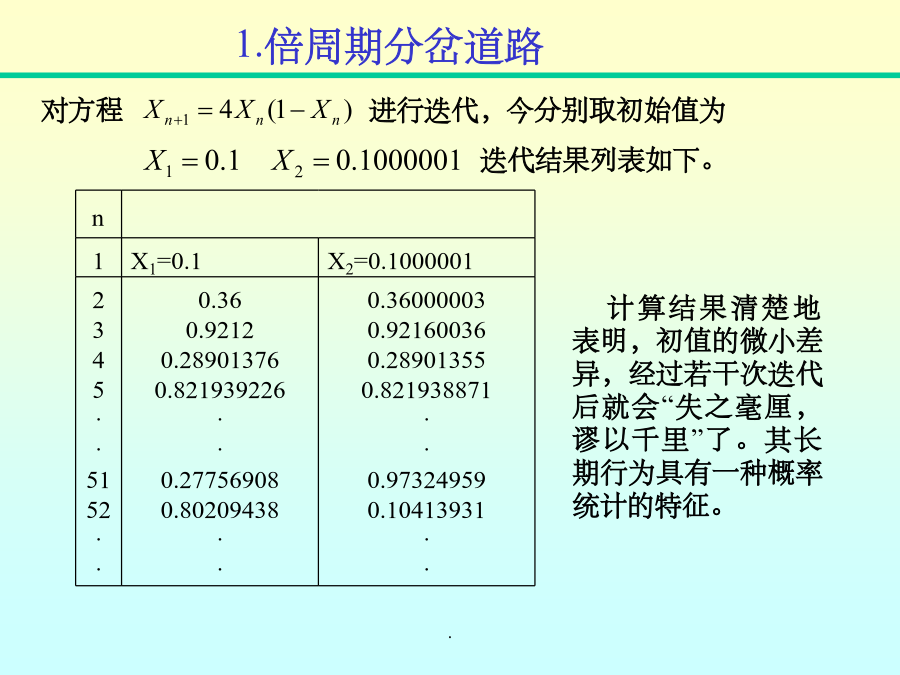
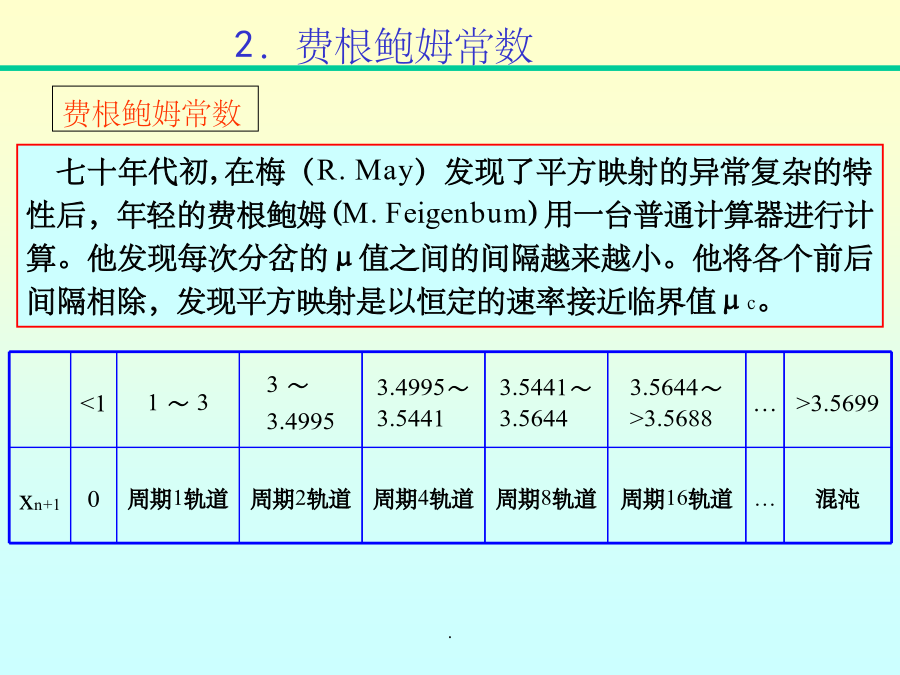
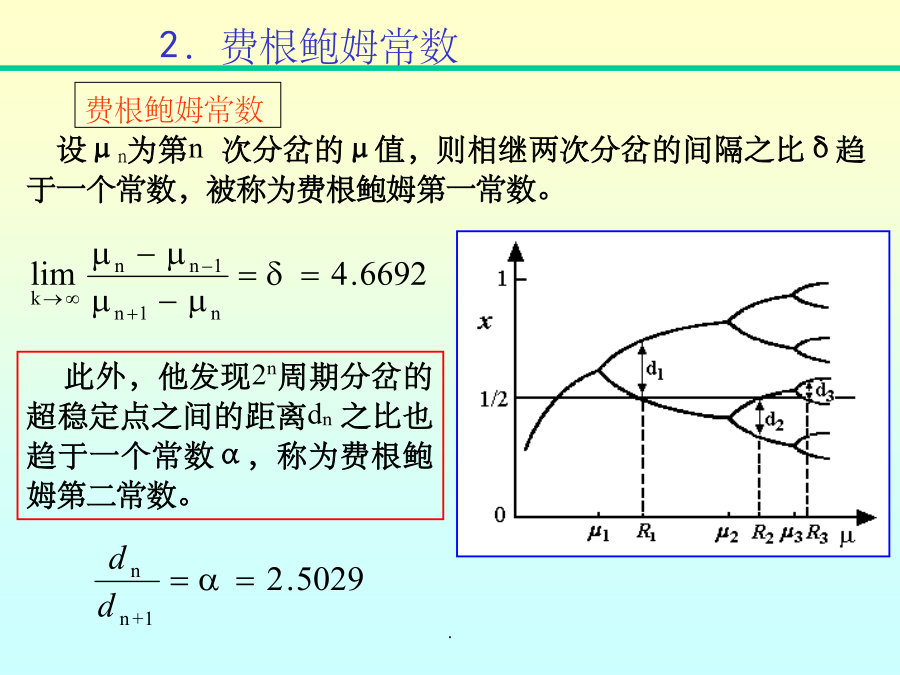
第3章走向混沌的道路混沌现象是一种普遍存在的复杂的运动形式。是确定论系统所表现的内在随机行为的总称，其根源在于系统内部的非线性交叉耦合作用，而不在于大量“分子”的无规则运动。1．平方映射的倍周期分岔道路
2．费根鲍姆常数
3．杜芬方程的倍周期分岔1.倍周期分岔道路平方映射的分岔图对方程倍周期分岔李氏指数费根鲍姆常数此外，他发现2n周期分岔的超稳定点之间的距离dn之比也趋于一个常数α，称为费根鲍姆第二常数。研究发现，对于所有在[0，1]区间内的单峰光滑映射，如正弦映射、圆与椭圆映射等，都可计算得同样常数。而且许多包含耗散的非线性系统，只要发生倍周期分岔也会有同样的常数。
两个费根鲍姆常数d与a都反映了非线性系统沿倍周期分岔系列通向混沌过程所具有的某种普适特性。可见费根鲍姆常数具有普遍意义。杜芬方程的倍周期分岔杜芬方程：

设γ=0.4,κ=1,ζ=4,F=0.115，从小到大改变驱动频率n。

计算表明，在n≥0.8时，杜芬方程的解是反对称的极限环，极限环呈椭圆形状；
当n<0.8时，极限环的反对称性虽然仍存在，但椭圆形状已明显变形。
当到达n≈0.535处时出现对称性破缺，极限环分裂为两个周期1的不对称极限环，这两个不对称的极限环互为反演。
在n≈0.53杜芬方程的解开始倍周期分岔。由于两个吸引子在n<0.53保持互为反演，可以在观察n<0.53时的分岔特性可以只考虑其中一个极限环。倍周期分岔第二节阵发性混沌自然界、科学实验乃至社会经济生活中，经常可以遇到突发性现象：太阳黑子、野生动物数量涨落、电子或激光振荡中的冲击现象，社会经济中的例子是股市的涨落。在非线性科学中是否相应的现象呢？
动力学系统经过突发性冲击现象进入随机的不规则的运动状态称为阵发性混沌(Intermittentchaos)。
1979年，法国数学家玻木(Pomeau)和曼维尔(Manneville)在计算洛论兹方程的y分量时发现：
当瑞利参数r在到达临界值rc附近时y分量的周期性变化被一种随机的、突发性的冲击所打断。当r<rc时，系统处于长时间周期运动状态；当r刚超过阈值rc时，开始偶尔出现一些突发性冲击；随着r数值的逐渐增长，这种突发性冲击越来越频繁，最后周期运动几乎完全消失，系统进入完全随机的运动状态。x-对流的翻动速率，
y-比例于上流与下流液体之间的温差
z-是垂直方向的温度梯度，
r-相对瑞利数r=R/RC。阵发现象(平方映射)平方映射的周期3窗口为解释阵发性混沌机理，需要分析平方映射在μ=3.83附近特性。类似于周期2，周期3可由三次平方映射f3(x)产生。

f3(x)有四个不动点，一个由f(x)带来的不稳定不动点，另外三个与迭代线相切。切点处f3(x)曲线的斜率为+1，是稳定性条件的最大值。μ稍许增大一点，,f3(x)将越过切点与迭代线相交为两个交点，产生出六个交点。相切点斜率为+1，每对相交的两个交点处斜率一个大于1，另一个小于1。根据稳定性条件，斜率大于1的轨道是不稳定的，小于1的是稳定的，即f3(x)有三个稳定不动点与三个不稳定的不动点。它们分别给出一条稳定的周期3轨道，和一条不稳定的周期3轨道。不稳定的周期3轨道已经退化。狭窄走廊中的迭代狭窄走廊中的迭代2.阵发性混沌机理