
人教版高中数学必修2立体几何复习精ppt课件.ppt

天马****23

亲,该文档总共102页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

人教版高中数学必修2立体几何复习精ppt课件.ppt
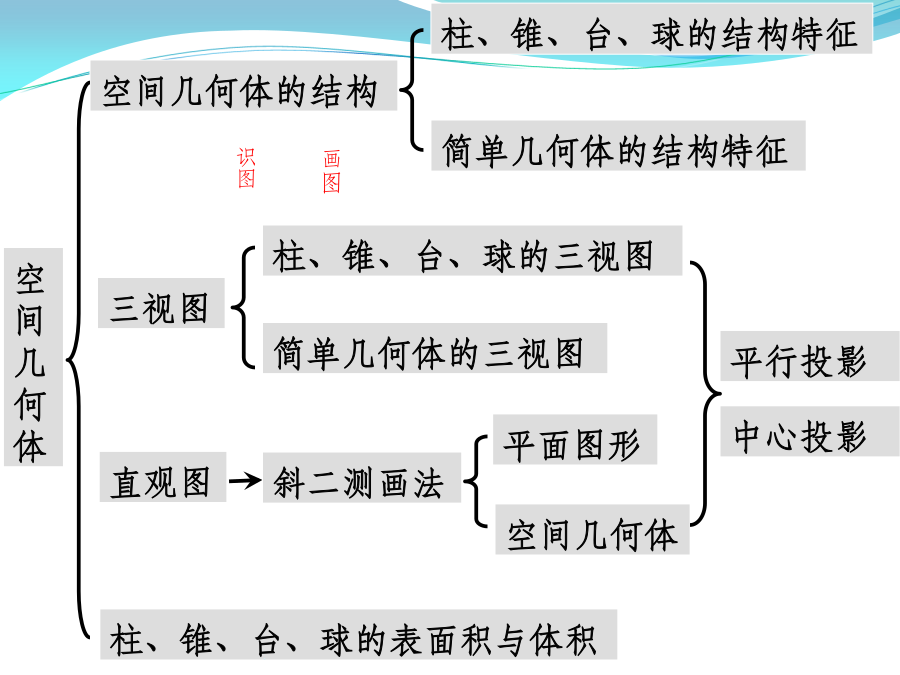
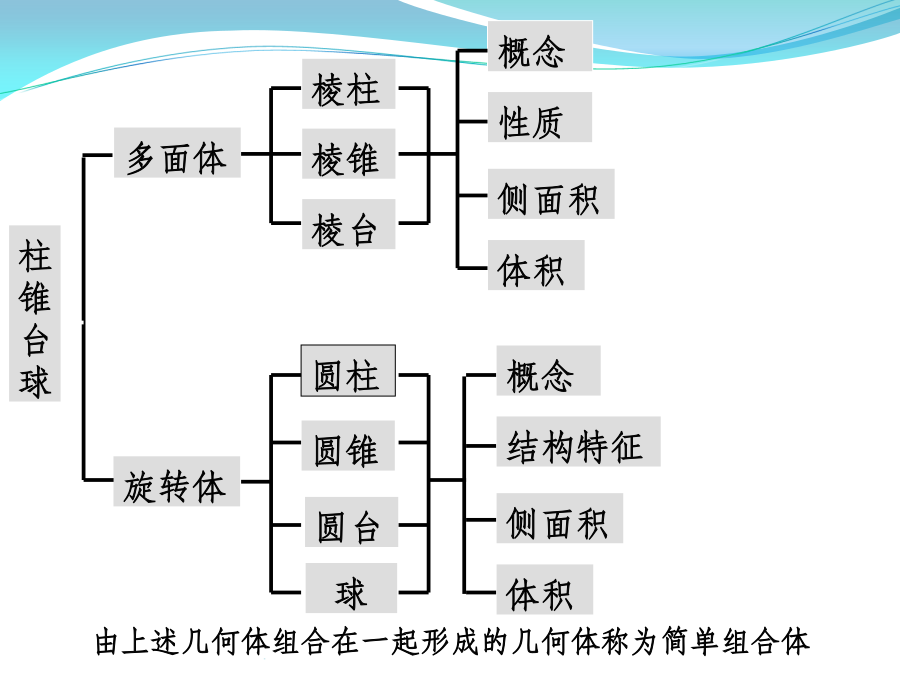
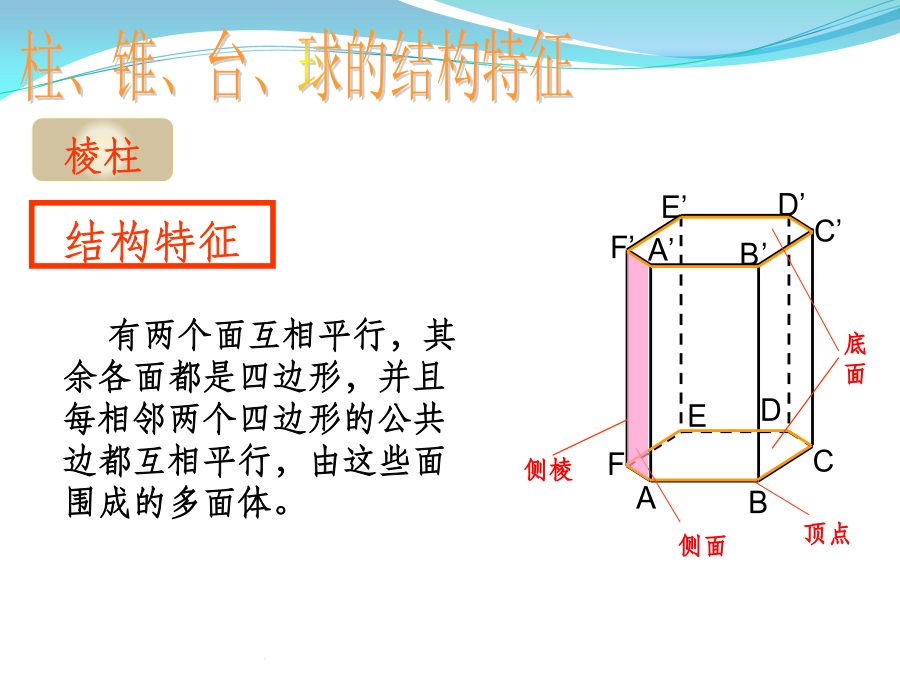
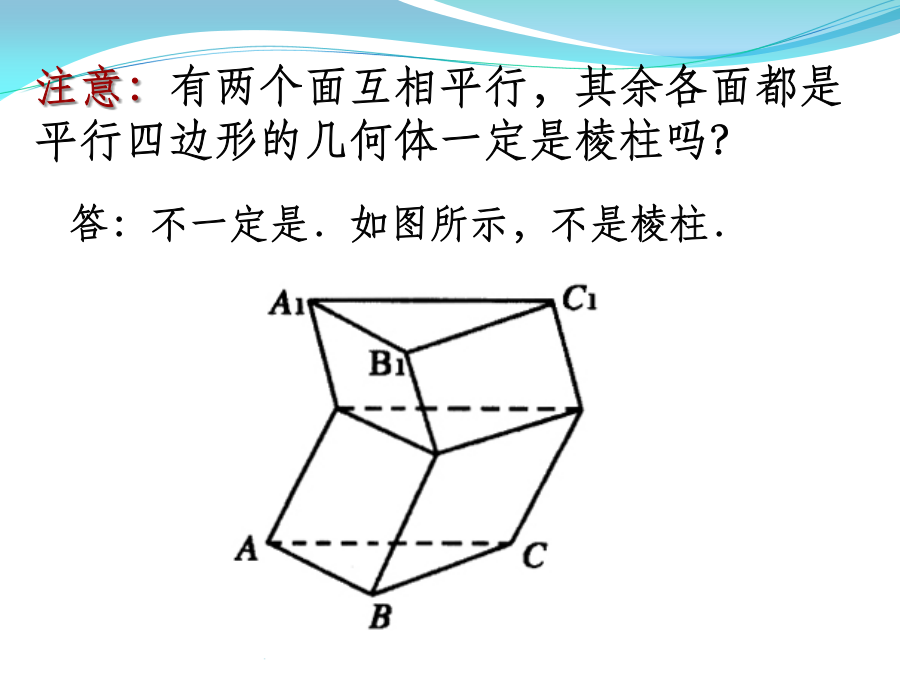
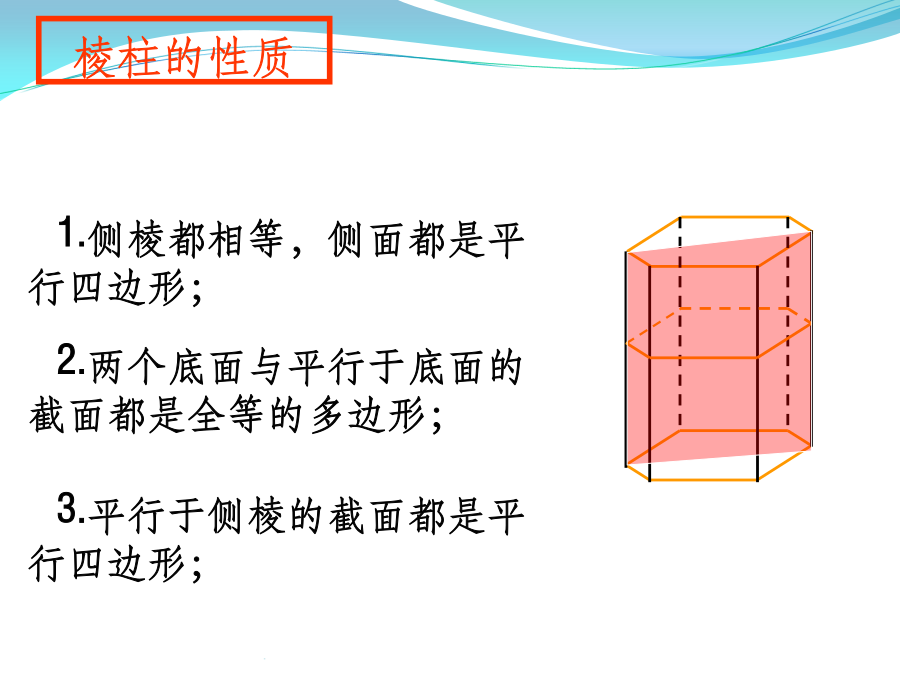
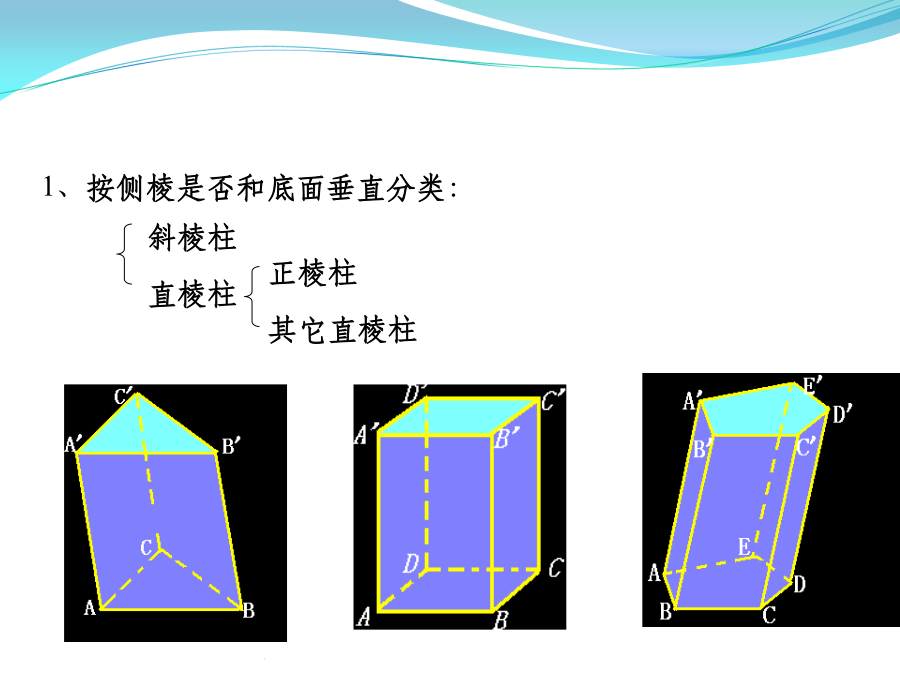
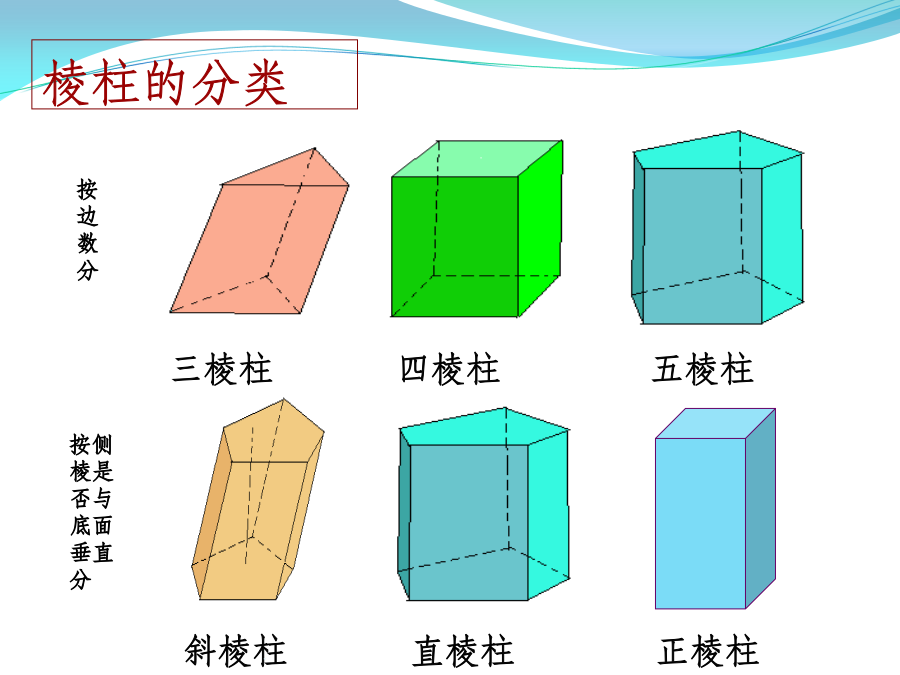
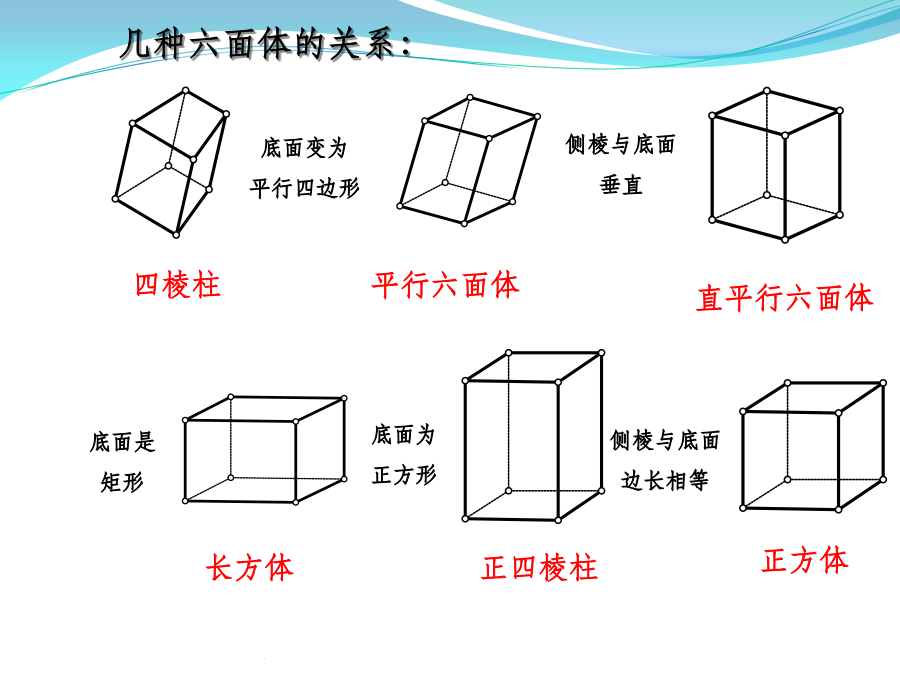
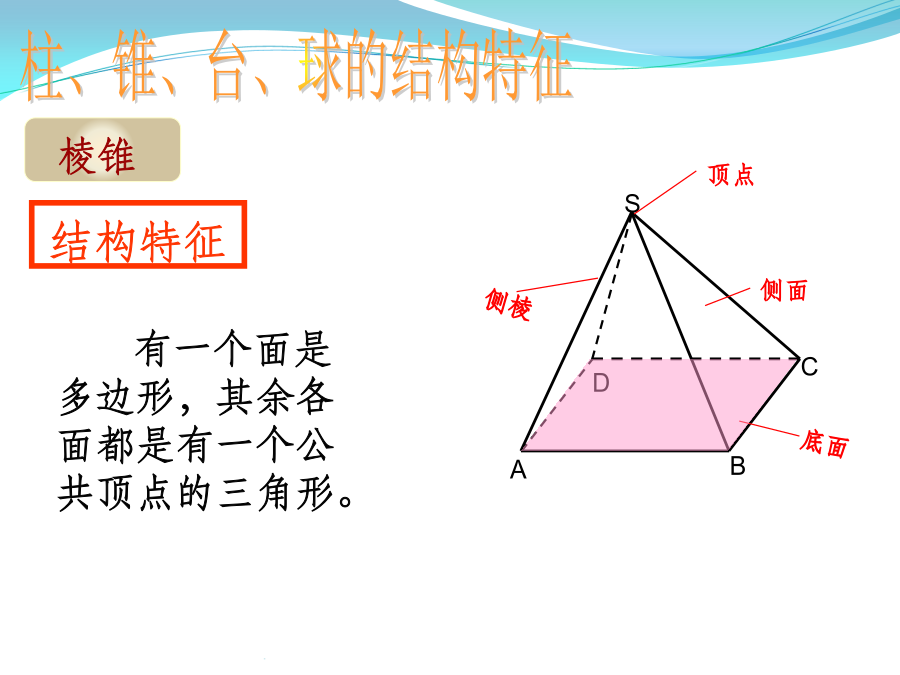
必修二复习(立体几何)空间几何体柱锥台球柱、锥、台、球的结构特征注意:有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱吗?棱柱的性质棱柱的分类四棱柱柱、锥、台、球的结构特征按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……【知识梳理】正棱锥性质2柱、锥、台、球的结构特征B’柱、锥、台、球的结构特征柱、锥、台、球的结构特征柱、锥、台、球的结构特征空间几何体的表面积和体积练习2.若一个锥体被平行于底面的平面所截,若截面面积是底面面积的四分之一,则锥体被截面截得的一个小锥与原棱锥体积之比为()(

人教版高中数学必修2立体几何复习完整ppt课件.ppt
必修二复习(立体几何)空间几何体柱锥台球柱、锥、台、球的结构特征注意:有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱吗?棱柱的性质棱柱的分类四棱柱柱、锥、台、球的结构特征按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……【知识梳理】正棱锥性质2柱、锥、台、球的结构特征B’柱、锥、台、球的结构特征柱、锥、台、球的结构特征柱、锥、台、球的结构特征空间几何体的表面积和体积练习2.若一个锥体被平行于底面的平面所截,若截面面积是底面面积的四分之一,则锥体被截面截得的一个小锥与原棱锥体积之比为()(

人教版高中数学必修2立体几何复习课件.ppt
必修二复习(立体几何)空间几何体柱锥台球柱、锥、台、球的结构特征注意:有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱吗?棱柱的性质棱柱的分类四棱柱柱、锥、台、球的结构特征按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……【知识梳理】正棱锥性质2柱、锥、台、球的结构特征B’柱、锥、台、球的结构特征柱、锥、台、球的结构特征柱、锥、台、球的结构特征空间几何体的表面积和体积练习2.若一个锥体被平行于底面的平面所截,若截面面积是底面面积的四分之一,则锥体被截面截得的一个小锥与原棱锥体积之比为()(

高中数学 必修2立体几何复习课件 新人教A必修2.ppt
立体几何复习课件平行问题平行问题直线和平面的位置关系直线在平面内平行于同一平面的二直线的位置关系是()(2)点A是直线l外的一点过A和直线l平行的平面有个。(3)过两条平行线中的一条和另一条平行的平面有个。(4)过两条异面直线中的一条和另一条平行的平面有个。(5)如果l1//l2l1平行于平面则l2平面线面平行的判定线面平行判定定理——如果平面外一条直线和这个平面内的一条直线平行那么这条直线和这个

高中数学 必修2立体几何复习课件 新人教A版必修2 课件.ppt
立体几何复习课件平行问题平行问题直线和平面的位置关系直线在平面内平行于同一平面的二直线的位置关系是()(1)点A是平面外的一点过A和平面平行的直线有条。(2)点A是直线l外的一点过A和直线l平行的平面有个。(3)过两条平行线中的一条和另一条平行的平面有个。(4)过两条异面直线中的一条和另一条平行的平面有个。(5)如果l1//l2l1平行于平面则l2平面线面平行的判定线面平行判定
