高中数学排列组合几种基本方法-豆柴文库

高中数学排列组合几种基本方法.ppt

2024-09-15

10金币

202KB

14页

天马****23

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共14页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

高中数学排列组合几种基本方法.ppt

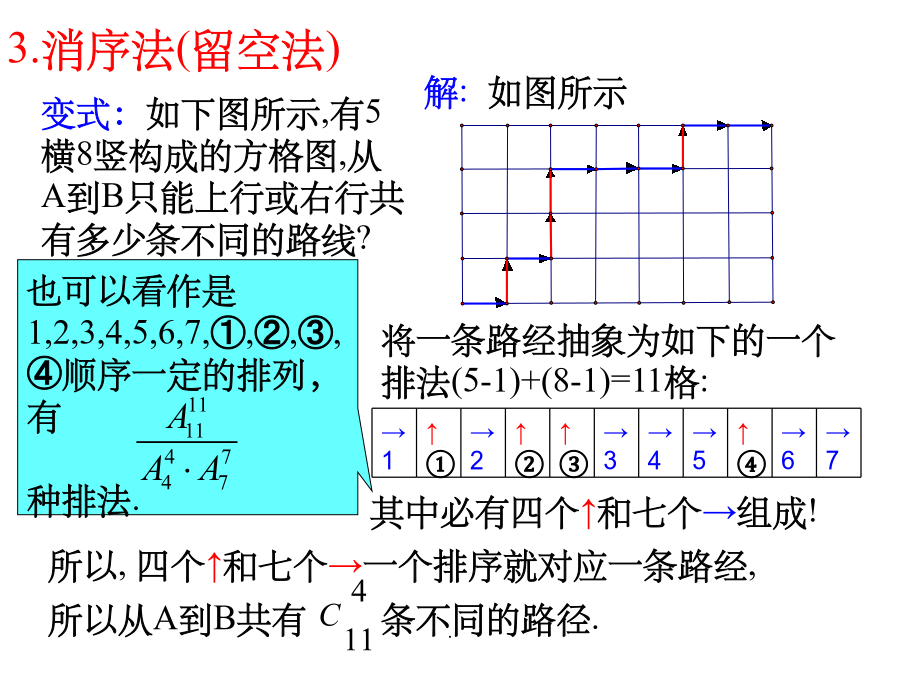
解排列组合的几种基本方法相邻元素的排列，可以采用“局部到整体”的排法，即将相邻的元素局部排列当成“一个”元素，然后再进行整体排列.例27人排成一排.甲、乙两人不相邻，有多少种不同的排法？例35个人站成一排，甲总站在乙的右侧的有多少种站法？变式：如下图所示,有5横8竖构成的方格图,从A到B只能上行或右行共有多少条不同的路线?④要明确堆的顺序（分配）时，必须先分堆后再把堆数当作元素个数作全排列.例4有四项不同的工程，要承包给三个工程队，要求每个工程队至少要得到一项工程.共有多少种不同的发包方式？n个相同小球放

2024-09-15

202KB

高中数学排列组合问题几种基本方法.pptx

2024-10-02

1.4MB

高中数学排列组合问题的几种基本方法.pdf

2024-09-02

473KB

排列组合几种基本方法.doc

排列组合几种基本方法1.直接法例1.用1，2，3，4，5，6这6个数字组成无重复的四位数，试求满足下列条件的四位数各有多少个（1）数字1不排在个位和千位（2）数字1不在个位，数字6不在千位。2.间接法当直接法求解类别比较大时，应采用间接法。例2有五张卡片，它的正反面分别写0与1，2与3，4与5，6与7，8与9，将它们任意三张并排放在一起组成三位数，共可组成多少个不同的三维书？3.插空法当需排元素中有不能相邻的元素时，宜用插空法。例3.在一个含有8个节目的节目单中，临时插入两个歌唱节目，且保持原节目顺序，有

2024-01-27

84KB

排列组合问题的几种基本方法.ppt

解排列组合问题的几种基本方法④要明确堆的顺序时，必须先分堆后再把堆数当作元素个数作全排列.例1.有四项不同的工程，要发包给三个工程队，要求每个工程队至少要得到一项工程.共有多少种不同的发包方式？例2.7人排成一排.甲、乙两人不相邻，有多少种不同的排法？相邻元素的排列，可以采用“局部到整体”的排法，即将相邻的元素局部排列当成“一个”元素，然后再进行整体排列.例4.5个人站成一排，甲总站在乙的右侧的有多少种站法？变式：如下图所示,有5横8竖构成的方格图,从A到B只能上行或右行共有多少条不同的路线?n个相同小球

2024-01-29

226KB