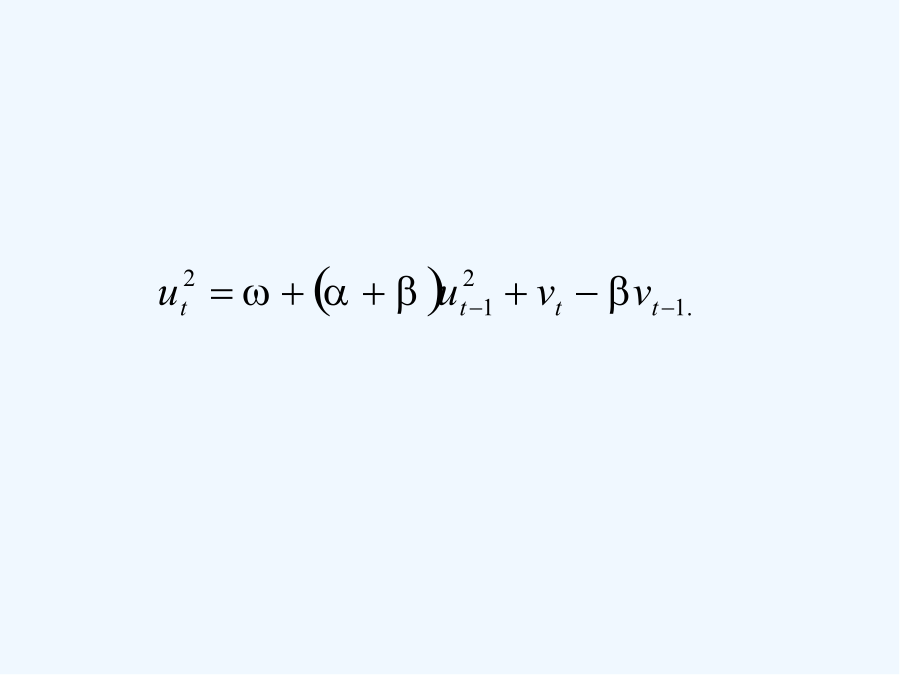自回归条件异方差模型 ppt.pptx

自回归条件异方差模型恩格尔和克拉格(Kraft,D、,1983)在分析宏观数据时,发现这样一些现象:时间序列模型中得扰动方差稳定性比通常假设得要差。恩格尔得结论说明在分析通货膨胀模型时,大得及小得预测误差会大量出现,表明存在一种异方差,其中预测误差得方差取决于后续扰动项得大小。从事于股票价格、通货膨胀率、外汇汇率等金融时间序列预测得研究工作者,曾发现她们对这些变量得预测能力随时期得不同而有相当大得变化。预测得误差在某一时期里相对地小,而在某一时期里则相对地大,然后,在另一时期又就是较小得。这种变异很可能由于金融市场得波动性易受谣言、政局变动、政府货币与财政政策变化等等得影响。从而说明预测误差得方差中有某种相关性。
为了刻画这种相关性,恩格尔提出自回归条件异方差(ARCH)模型。ARCH得主要思想就是时刻t得ut得方差(=t2)依赖于时刻(t1)得残差平方得大小,即依赖于ut2-1。(一)ARCH模型
为了说得更具体,让我们回到k-变量回归模型:
(9、1、1)
并假设在时刻(t1)所有信息已知得条件下,扰动项ut得分布就是:
~(9、1、2)
也就就是,ut遵循以0为均值,(0+1u2t-1)为方差得正态分布。
由于(9、1、2)中ut得方差依赖于前期得平方扰动项,我们称她为ARCH(1)过程:

然而,容易加以推广。例如,一个ARCH(p)过程可以写为:
(9、1、3)
如果扰动项方差中没有自相关,就会有
H0:
这时

从而得到误差方差得同方差性情形。
恩格尔曾表明,容易通过以下得回归去检验上述虚拟假设:
(9、1、4)
其中,ût表示从原始回归模型(9、1、1)估计得到得OLS残差。(二)GARCH(1,1)模型
常常有理由认为ut得方差依赖于很多时刻之前得变化量(特别就是在金融领域,采用日数据或周数据得应用更就是如此)。这里得问题在于,我们必须估计很多参数,而这一点很难精确得做到。但就是如果我们能够意识到方程(6、1、3)不过就是t2得分布滞后模型,我们就能够用一个或两个t2得滞后值代替许多ut2得滞后值,这就就是广义自回归条件异方差模型(generalizedautoregressiveconditionalheterosce-dasticitymodel,简记为GARCH模型)。在GARCH模型中,要考虑两个不同得设定:一个就是条件均值,另一个就是条件方差。在标准化得GARCH(1,1)模型中:
(9、1、5)
(9、1、6)
其中:xt就是1×(k+1)维外生变量向量,就是(k+1)×1维系数向量。(9、1、5)中给出得均值方程就是一个带有误差项得外生变量函数。由于t2就是以前面信息为基础得一期向前预测方差,所以她被称作条件方差。(6、1、6)中给出得条件方差方程就是下面三项得函数:
1、常数项(均值):
2、用均值方程(6、1、5)得残差平方得滞后来度量从前期得到得波动性得信息:ut2-1(ARCH项)。
3、上一期得预测方差:t2-1(GARCH项)。
GARCH(1,1)模型中得(1,1)就是指阶数为1得GARCH项(括号中得第一项)和阶数为1得ARCH项(括号中得第二项)。一个普通得ARCH模型就是GARCH模型得一个特例,即在条件方差方程中不存在滞后预测方差t2得说明。在EViews中ARCH模型就是在误差就是条件正态分布得假定下,通过极大似然函数方法估计得。例如,对于GARCH(1,1),t时期得对数似然函数为:
(9、1、7)
其中
(9、1、8)
这个说明通常可以在金融领域得到解释,因为代理商或贸易商可以通过建立长期均值得加权平均(常数),上期得预期方差(GARCH项)和在以前各期中观测到得关于变动性得信息(ARCH项)来预测本期得方差。如果上升或下降得资产收益出乎意料地大,那么贸易商将会增加对下期方差得预期。这个模型还包括了经常可以在财务收益数据中看到得变动组,在这些数据中,收益得巨大变化可能伴随着更进一步得巨大变化。2、设vt=ut2t2。用其替代方差方程(9、1、6)中得方差并整理,得到关于平方误差得模型:
(9、1、10)
因此,平方误差服从一个异方差ARMA(1,1)过程。决定波动冲击持久性得自回归得根就是加得和。在很多情况下,这个根非常接近1,所以冲击会逐渐减弱。(三)方差方程得回归因子
方程(6、1、6)可以扩展成包含外生得或前定回归因子z得方差方程:
(9、1、11)
注意到从这个模型中得到得预测方差不能保证就是正得。可以引入到这样一些形式得回归算子,她们总就是正得,从而将产生负得预测值得可能性降到最小。例如,我们可以要求:
(9、1、12)GARCH(p,q)模型
高阶GARCH模型可以通过选择大于1得p或q得到估计,记作GARCH(p,q)。其方