基于张量的非局部自相似和低秩正则的张量修复方法.pdf

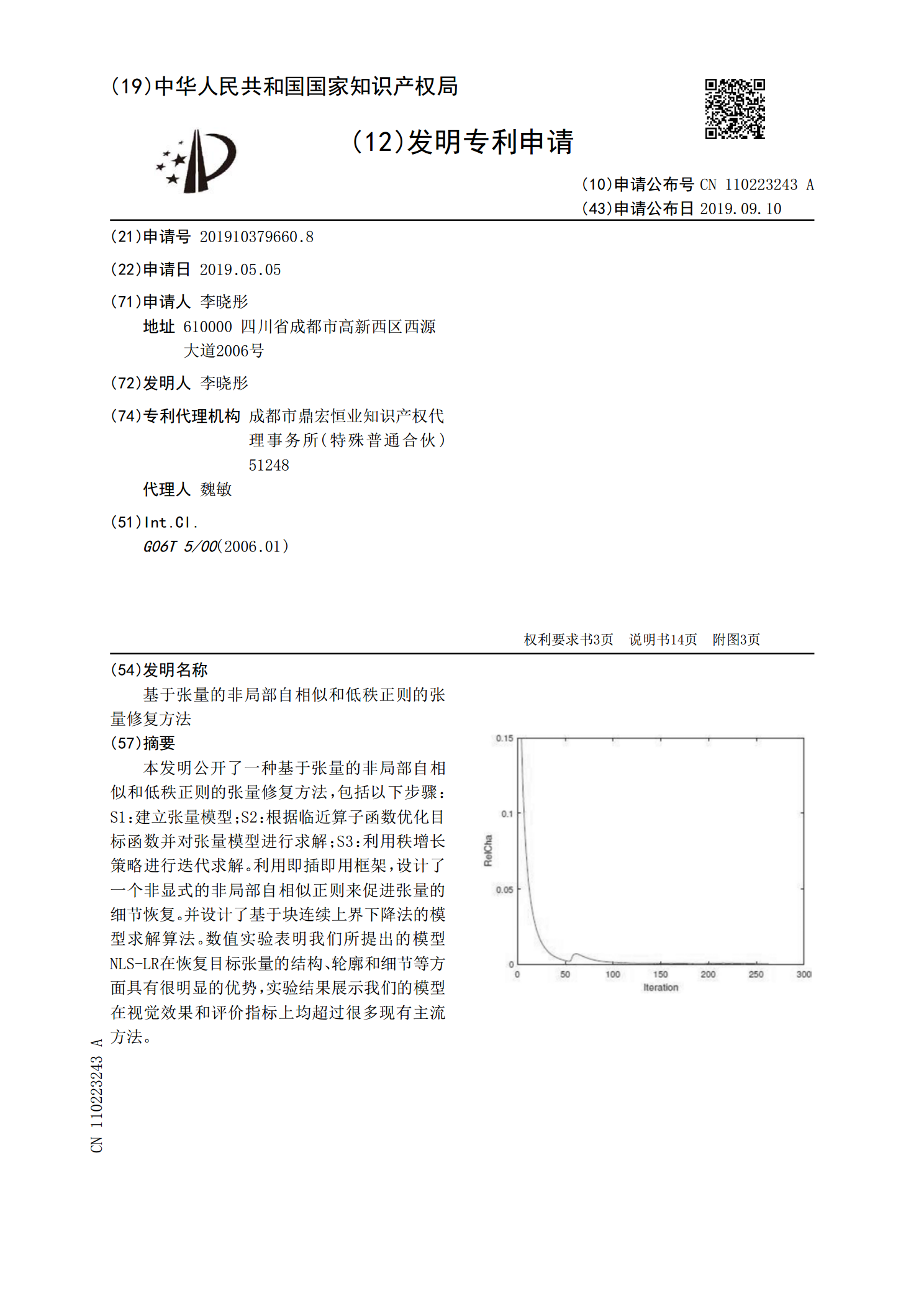
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号CN110223243A(43)申请公布日2019.09.10(21)申请号201910379660.8(22)申请日2019.05.05(71)申请人李晓彤地址610000四川省成都市高新西区西源大道2006号(72)发明人李晓彤(74)专利代理机构成都市鼎宏恒业知识产权代理事务所(特殊普通合伙)51248代理人魏敏(51)Int.Cl.G06T5/00(2006.01)权利要求书3页说明书14页附图3页(54)发明名称基于张量的非局部自相似和低秩正则的张量修复方法(57)摘要本发明公开了一种基于张量的非局部自相似和低秩正则的张量修复方法，包括以下步骤：S1：建立张量模型；S2：根据临近算子函数优化目标函数并对张量模型进行求解；S3：利用秩增长策略进行迭代求解。利用即插即用框架，设计了一个非显式的非局部自相似正则来促进张量的细节恢复。并设计了基于块连续上界下降法的模型求解算法。数值实验表明我们所提出的模型NLS-LR在恢复目标张量的结构、轮廓和细节等方面具有很明显的优势，实验结果展示我们的模型在视觉效果和评价指标上均超过很多现有主流方法。CN110223243ACN110223243A权利要求书1/3页1.一种基于张量的非局部自相似和低秩正则的张量修复方法，其特征在于：包括以下步骤：S1：建立张量模型；S2：根据临近算子函数优化目标函数并对张量模型进行求解；S3：利用秩增长策略进行迭代求解。2.根据权利要求1所述的基于张量的非局部自相似和低秩正则的张量修复方法，其特征在于：所述S1步骤中建立张量模型的具体方法是：针对三维的张量建立模型为其中αn是非负权重，满足Y(n)代表沿张量不同方向的展开矩阵；A＝(A1,A2,A3)和X＝(X1,X2,X3)代表沿张量不同方向的低秩因子矩阵，λ是正则参数，是非局部自相似性正则，是指示函数，满足3.根据权利要求1所述的基于张量的非局部自相似和低秩正则的张量修复方法，其特征在于：所述S2步骤根据临近算子函数优化目标函数并对张量模型进行求解的方法是：根据临近算子函数优化目标函数：其中ρ是临近算子参数；通过使用块连续上界下降法，求解如下：对于Xn和An的子问题：转化为如何求解的子问题，即2CN110223243A权利要求书2/3页矩阵的Frobenius范数是所有元素额算术平方根之和，如果定义为矩阵沿第n方向的折叠张量，那么矩阵的Frobenius范数和张量Frobenius范数是相等的，则得到的子问题转化为如下形式：进一步将目标函数转化成如下形式：其中是矩阵沿第n个方向折叠的张量；现令此时的子问题改写成：是通过即插即用框架设计的非局部自相似正则，那么目标函数通过以下公式求解：通过投影函数来将结果投影到可行域来满足约束条件，至此子问题的解为如下形式：其中是投影函数，是即插即用算子函数，σ是控制正则项强度的参数。4.根据权利要求1所述的基于张量的非局部自相似和低秩正则的张量修复方法，其特征在于：所述S3步骤中利用秩增长策略进行迭代的方法是：以秩作为初始，当迭代的相对误差小于设定的阈值时，即：3CN110223243A权利要求书3/3页把对应的秩rn在第k+1迭代更新为其中Δrn是正整数、是Tucker秩上界；当rn在第k+1次迭代中增加时，将更新为同时，将更新为将rn更新为即添加大小为Δrn的随机矩阵到的列向量组，添加大小为Δrn的随机矩阵到的行向量组。4CN110223243A说明书1/14页基于张量的非局部自相似和低秩正则的张量修复方法技术领域[0001]本发明涉及图像处理技术领域，具体涉及一种基于张量的非局部自相似和低秩正则的张量修复方法。背景技术[0002]在如今的信息化社会中，信息呈爆炸式增长。现实生活中如核磁共振图像(MRI)、高光谱图/多光谱图(HSI/MSI)、彩色图片和视频等数据往往具有高维的结构。作为向量和矩阵的推广，张量在表示高维的数据中具有非常重要的作用。由于信息缺失或者获取信息代价过大，现实生活中的张量往往表现出一种不完整的结构。从缺失张量出发推测得到完整张量的问题叫做张量修复问题(LRTC)。张量修复问题在现实中有广泛的应用，如图片修复、核磁共振图像复原、去雨和遥感卫星图像修复等。[0003]为了解决张量修复问题，我们需要挖掘缺失张量中已知点与未知点间的内在联系。实际上，数据往往存在很强的内在关联，我们一般称之为低秩性。近年来有许多利用刻画已知点和未知点间联系的方法，已经在张量修复问题上取得了很好的进展。从数学模型的角度看，低秩张量修复问题可以被表述为：[0004][0005]其中是目标张量，是观测张量，Ω是已知点所在的观测集，是投影函数(可以使得观测集中的元素保持不变，其余的元素置为0)。事实上