
一种高能罗茨泵用外直转子.pdf

一吃****新冬









亲,该文档总共14页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

一种高能罗茨泵用外直转子.pdf
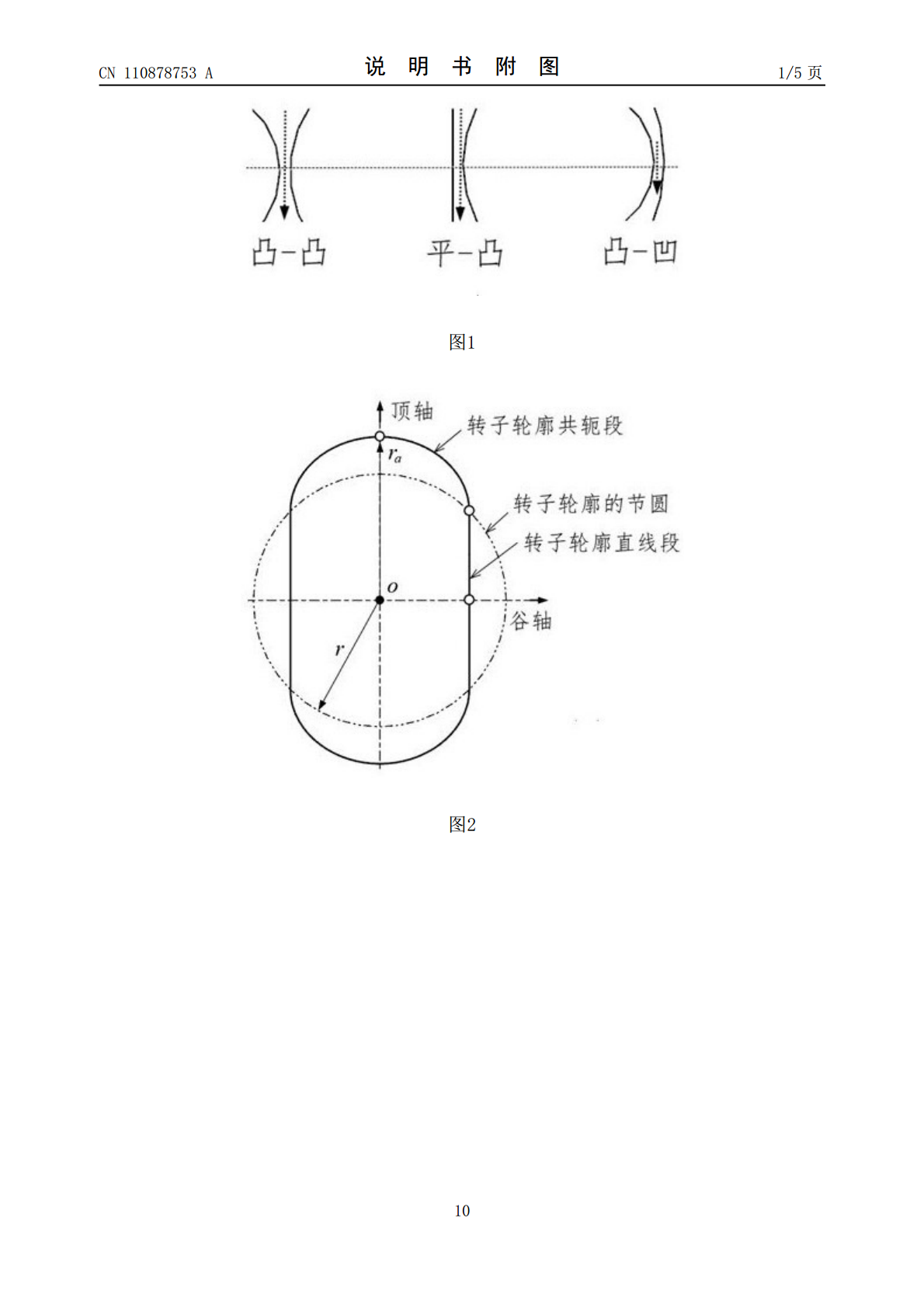
本发明公开了一种高能罗茨泵用外直转子,包括转子本体和与之完全相同的共轭体,所述转子本体的轮廓由半叶轮廓镜像后圆周阵列设置,所述半叶轮廓由节圆外侧的第一圆弧段、第一过渡圆弧段、第二过渡圆弧段、直线段、节圆内侧的第一曲线段、第二曲线段和第二圆弧段组成;所述直线段的起点法线过转子顶轴与节圆的交点,终点位于节圆上,其陡峭程度由起点法线与转子顶轴间的夹角所唯一确定,本发明结构简单、通过本发明设计的转子轮廓,能实现转子更大的形状系数及对应的容积利用系数,降低的内泄漏率尤其径向泄漏率和共轭泄漏。

罗茨泵转子.pdf
本发明涉及一种罗茨泵,特别涉及一种罗茨泵转子,包括本体,本体为二叶式,本体型线包括依次设置的第一圆弧段、共轭曲线段、渐开线段、第二圆弧段、第三圆弧段,第一圆弧段、共轭曲线段、渐开线段、第二圆弧段、第三圆弧段之间平滑连接。本发明通过设置渐开线段、第二圆弧段,大大降低了啮合点数,使转子型线干涉几率大大降低,避免转子卡死,使加工和装配更加容易。

一种单头扭叶罗茨泵转子及罗茨泵.pdf
一种单头扭叶罗茨泵转子及罗茨泵,单头扭叶罗茨泵转子包括相互啮合的第一转子和第二转子,第一转子的型线为偏心圆形结构,第二转子的型线为第一转子型线的包络线;第一转子和第二转子均为扭叶型,扭转方向相反;第一转子和第二转子分别沿各自转子型线以螺旋线为引导线扫描形成;第一转子和第二转子按照各自转轴以相同角速度异向旋转。一种罗茨泵,包括泵体,泵体内部开设有泵腔,泵腔能够容纳所述的单头扭叶罗茨泵转子,泵体上开设与泵腔连通的吸气孔口和排气孔口;第一转子和第二转子与泵腔形成封闭空间,啮合运行过程中由吸气孔口抽气,在泵腔内对

一类罗茨泵用的双曲线转子.pdf
本发明涉及一类罗茨泵用的双曲线转子,由2叶或3叶或4叶的一对双曲线转子副构成,其半叶理论轮廓均由节圆外侧的圆弧段12、过渡圆弧段23、过渡圆弧段34、双曲线段45,节圆内侧的曲线段56、曲线段67和圆弧段78,共首尾相连的7段轮廓段组成。本发明双曲线转子叶的重心明显偏向谷部,转子系统的动平衡性能好,且容积利用系数高、脉动质量好。本发明容积利用率高,综合性能好。

带转子冷却结构的罗茨泵.pdf
本发明公开了一种带转轴冷却结构的罗茨泵,旨在解决现有的罗茨泵对转轴的冷却效果较差,罗茨泵使用寿命短的不足。该发明包括泵体,泵体的前后两端分别连接有前侧盖和后侧盖,前侧盖上连接前盖,后侧盖上连接后盖,前盖和后盖之间连接有转轴,转轴上连接有转子,前盖内设有前盖腔,前侧盖内设有前冷却腔,后盖内设有后盖腔,后侧盖内设有后冷却腔,前盖腔和前冷却腔连通,后盖腔和后冷却腔连通,转子呈8字形结构,转子内设有两个封闭的转子冷却腔,转子冷却腔的两端分别与前冷却腔和后冷却腔连通,转子上靠近进液孔位置套接有用于带动冷却液的离心叶
