
最小相位系统.ppt

qw****27









亲,该文档总共13页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

最小相位系统.ppt
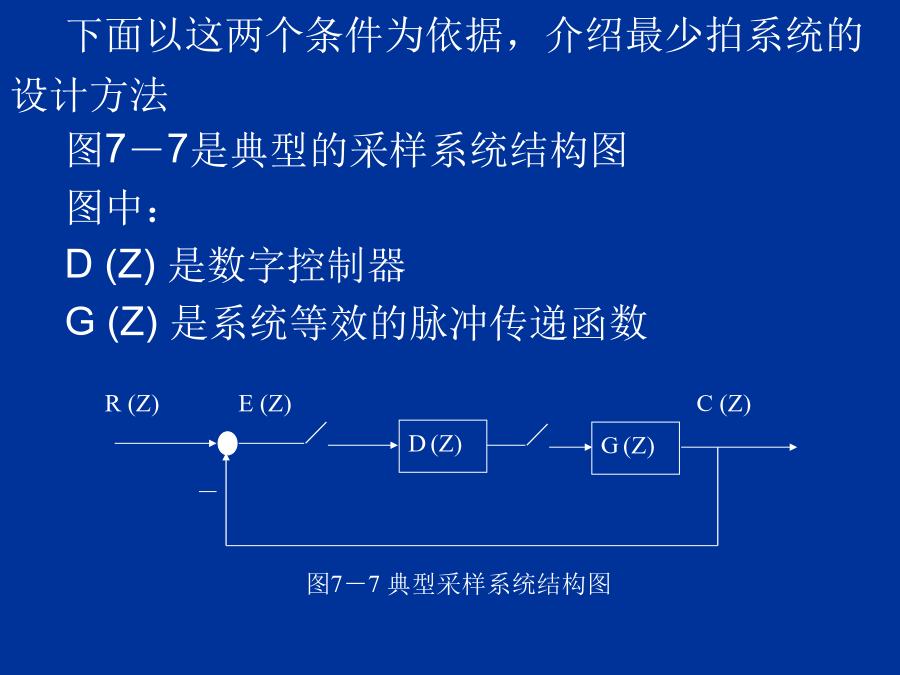
控制工程基础7.6采样系统的校正图7-6是两个系统的输出曲线对比图,图中:曲线1只用1拍达到稳态曲线2用了2拍达到稳态曲线1所代表的系统称为最少拍系统从最少拍系统的概念可知,最少拍系统应满足两个条件:①稳态误差为零②调节时间最短下面以这两个条件为依据,介绍最少拍系统的设计方法图7-7是典型的采样系统结构图图中:D(Z)是数字控制器G(Z)是系统等效的脉冲传递函数2.先讨论如何使系统的稳态误差为零由图可知,误差信号E(Z)为(7-10)根据终值定理可求得系统的稳态误差为(7-11)显然,稳态误差的大小与输入

最小相位系统.ppt
控制工程基础7.6采样系统的校正图7-6是两个系统的输出曲线对比图,图中:曲线1只用1拍达到稳态曲线2用了2拍达到稳态曲线1所代表的系统称为最少拍系统从最少拍系统的概念可知,最少拍系统应满足两个条件:①稳态误差为零②调节时间最短下面以这两个条件为依据,介绍最少拍系统的设计方法图7-7是典型的采样系统结构图图中:D(Z)是数字控制器G(Z)是系统等效的脉冲传递函数2.先讨论如何使系统的稳态误差为零由图可知,误差信号E(Z)为(7-10)根据终值定理可求得系统的稳态误差为(7-11)显然,稳态误差的大小与输入

第12讲bode最小相位系统和非最小相位系统.pptx
第12讲程向红第5章线性系统的频域分析法Frequency-responseanalysis5.1.2频率特性的表示法极坐标图(Polarplot)=幅相频率特性曲线=幅相曲线5.2典型环节频率特性曲线的绘制5.2.2积分与微分因子5.2.3一阶因子5.2.4二阶因子图5-15开环系统的伯德图45.2.5最小相位系统与非最小相位系统对于最小相位系统其传递函数由单一的幅值曲线唯一确定。对于非最小相位系统则不是这种情况。非最小相位系统在具有相同幅值特性的系统中最小相位传递函数(系统)的

非最小相位系统的复杂控制算法研究.docx
非最小相位系统的复杂控制算法研究非最小相位系统的复杂控制算法研究摘要:非最小相位系统是指具有多个零点或者零点与极点分布不均匀的系统。这种系统在控制过程中会带来一定的困难,因为其频率响应的相位特性比最小相位系统复杂。因此,针对非最小相位系统的复杂控制算法研究成为了一个重要的研究方向。本文将从非最小相位系统的定义、特点以及现有的复杂控制算法进行分析和综述,并对未来的研究方向进行展望。1.引言非最小相位系统是指其频率响应的相位特性比最小相位系统复杂的系统。它们具有多个零点或者零点与极点分布不均匀,这导致在控制过

最小相位系统(精品文档)-共2页.pdf
最小相位系统(MinimumPhaseSystems)定义:如果控制系统的所有极点和零点均位于s左半平面上,则称该系统为最小相位系统。一个系统被称为最小相位系统,当且仅当这个系统是因果稳定的,有一个有理形式的系统函数,并且存在着一个因果稳定的逆函数。特点:特点1:如果两个系统有相同的幅频特性,那么对于大于零的任何频率,最小相位系统的相角总小于非最小相位系统;特点2:最小相位系统的幅频特性和相频特性直接关联,也就是说,一个幅频特性只能有一个相频特性与之对应,一个相频特性只能有一个幅频特性与之对应。对于最小相
