通信原理第8讲.pdf

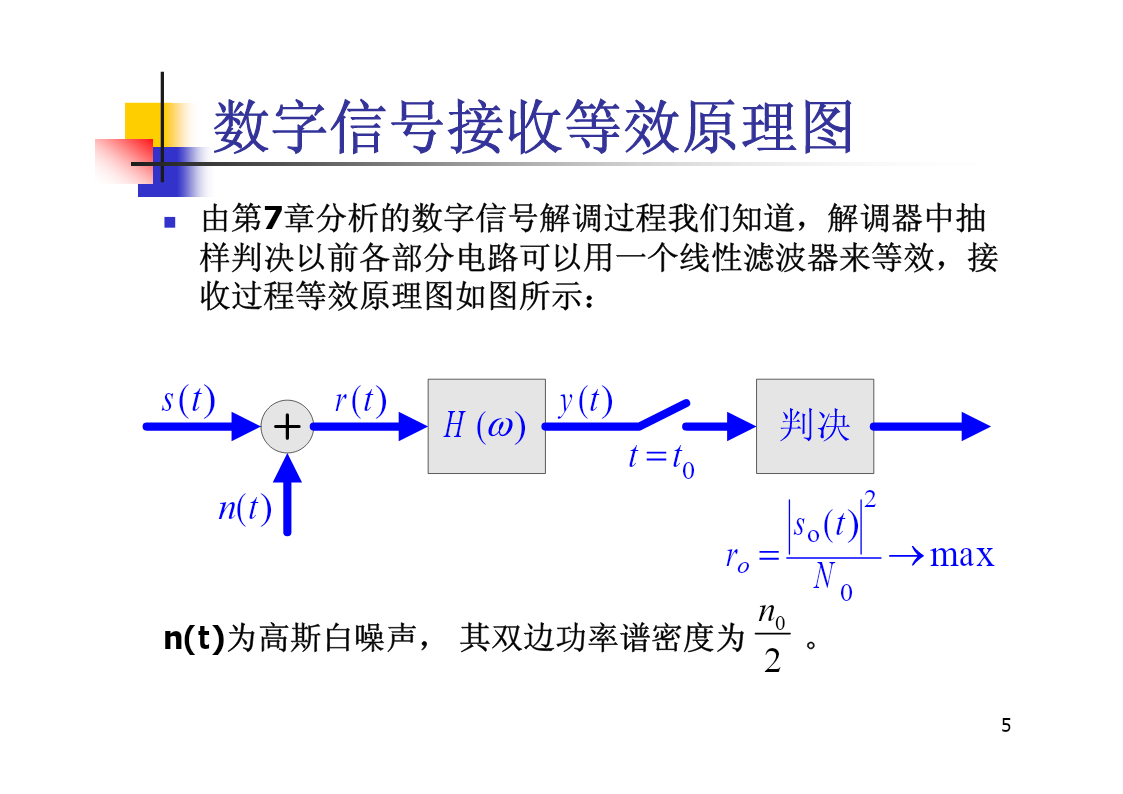
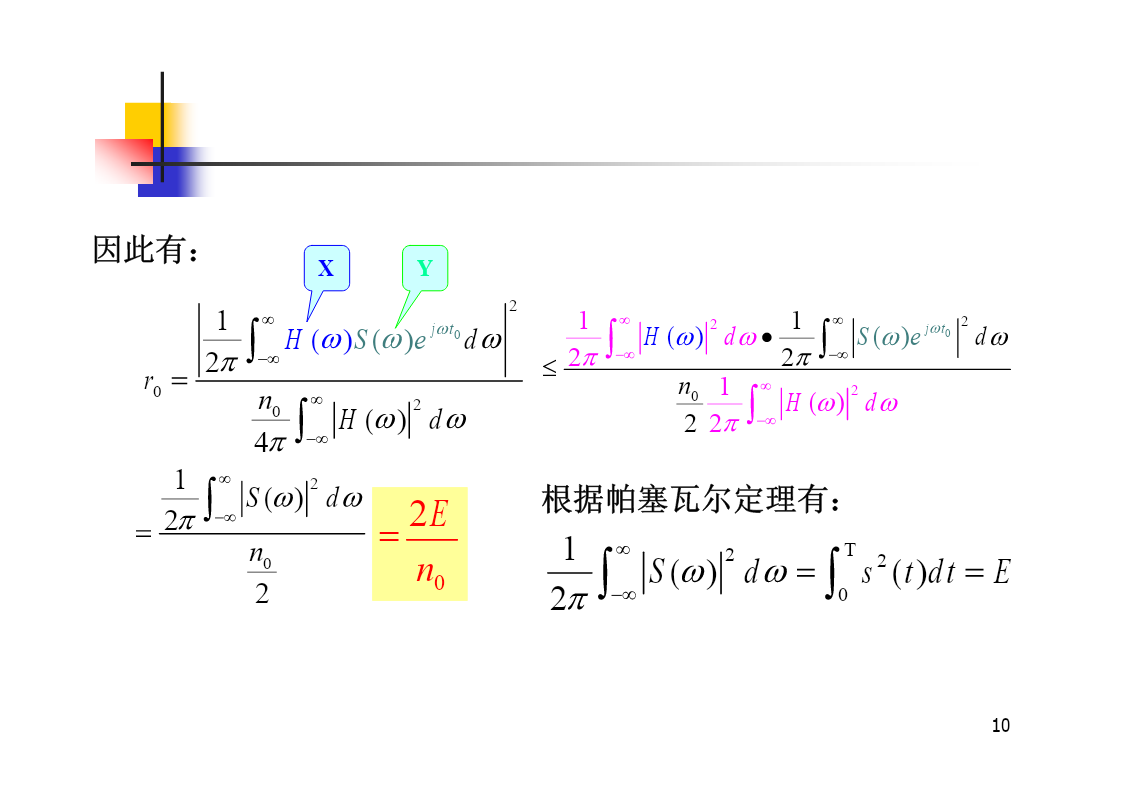
第八章数字信号的最佳接收
内容提要

§8.1匹配滤波器
§8.2最小差错概率接收准则
§8.3确知信号的最佳接收机
§8.4随相信号的最佳接收机
§8.5最佳接收机的性能比较

作业：1、3、4、8、9、10、11、14

2
概述

在通信系统中，信道特性不理想以及存在信道噪声，直接
影响接收系统的性能。

一个通信系统质量的优劣在很大程度上取决于接收系统的
性能。
提高接收系统的性能——最佳接收。

„在噪声条件下，如何最好地提取有用信号，且在某个准则下构成
最佳接收机，使接收性能达到最优。

所谓最佳是在某种标准下系统性能达到最佳，最佳标准也
称最佳准则。

最佳接收是一个相对的概念，在某种准则下的最佳系统，
在另外一种准则下就不一定是最佳的。

在数字通信中，最常采用的最佳准则是输出信噪比最大准
则和差错概率最小准则。

3
§8.1匹配滤波器

在数字通信系统中，滤波器是其中重要部件之一，滤波器
特性的选择直接影响数字信号的恢复。

在数字信号接收中，滤波器的作用有两个方面：

„第一是使滤波器输出有用信号成分尽可能强；

„第二是抑制信号带外噪声，使滤波器输出噪声成分尽可能小，减
小噪声对信号判决的影响。

通常对最佳线性滤波器的设计有两种准则：

„一种是使滤波器输出的信号波形与发送信号波形之间的均方误差
最小，由此而导出的最佳线性滤波器称为维纳滤波器；

„另一种是使滤波器输出信噪比在某一特定时刻达到最大，由此而
导出的最佳线性滤波器称为匹配滤波器。

„在数字通信中，匹配滤波器具有更广泛的应用。

4
数字信号接收等效原理图

„由第7章分析的数字信号解调过程我们知道，解调器中抽
样判决以前各部分电路可以用一个线性滤波器来等效，接
收过程等效原理图如图所示：

st()rt()yt()
H()ω判决
tt=0
nt()2
sto()
r=→max
oN
n0
n(t)为高斯白噪声，其双边功率谱密度为0。
2

5
由数字信号的判决原理我们知道，

抽样判决器输出数据正确与否，与滤波器输出信号波形和
发送信号波形之间的相似程度无关，也即与滤波器输出信
号波形的失真程度无关，

而只取决于抽样时刻信号的瞬时功率与噪声平均功率之
比，即信噪比。

„信噪比越大，错误判决的概率就越小；

„信噪比越小，错误判决的概率就越大。

为了使错误判决概率尽可能小，就要选择滤波器传输特性
使滤波器输出信噪比尽可能大的滤波器。

下面就来分析当滤波器具有什么样的特性时才能使输出信
噪比达到最大。

6
问题

匹配滤波器的传输函数=？

匹配滤波器的单位冲激响应=？

匹配滤波器的输出信号=？

7
匹配滤波器的传输函数

匹配滤波器的输入信号为：r(t)=s(t)+n(t)

匹配滤波器的输出信号为：y(t)=s0(t)+n0(t)

1∞1∞
其中：st()=S()ωejtωdω=S()ωωH()ejtωdω
02π∫−∞02π∫−∞

滤波器输出噪声的平均功率为：

1∞1∞2
N=P(ω)dω=Pn(ω)H()ωdω
02π∫−∞n02π∫−∞i

1∞n2
=0H()ωdω
2π∫−∞2
8
2
∞
1jtω
2HSed()()ωωω0
抽样时刻的输出信噪比：∫−∞
st00()2π
r0==
Nn1∞2
00Hd()ωω
22π∫−∞
利用许瓦尔兹不等式：
2
1∞1∞21∞2
X(ω)Y(ω)dω≤X(ω)dωY(ω)dω
2π∫−∞2π∫−∞2π∫−∞

等号成立的条件：X(ω)=KY*(ω)K为不等于0的常数：

9
因此有：
XY
2
∞∞
1∞121jtω2
H()ωS()ωejtω0dωH()ωdω•Se(ω)0dω
∫−∞∫−∞∫−∞
2π≤2π2π
r=n∞2
0∞01
n02Hd()ωω
H()ωωd22π∫−∞
4π∫−∞
1∞2
Sd()ωω根据帕塞瓦尔定理有：
∫−∞
=2π2E
=∞T
n0122
n0Sd()ωω=stdtE()=
22π∫∫−∞0

10
不等号成立的条件是：

HKSe()ωω=*()−jtω0

2E
ro,max=
n0

S*(ω)是输入信号频谱函数S(ω)的复共轭。

11
匹配滤波器的单位冲激响应

∞1∞
1jtω=KeS*()ω−jωt0edjωtω
ht()=H()ωedω∫−∞
2π∫−∞2π
K∞∞*
=⎡⎤se()ττ−jωτded−−jttω(0)ω
2π∫−∞⎣⎦⎢⎥∫−∞

∞∞
⎡⎤1jttωτ()−+0
=Kedsd⎢⎥ω()ττ
∫∫−∞⎣⎦2π−∞

∞
=−+Ks()(τδτttd)τ
∫−∞0

K=1
ht()=st(−t)
ht()=Kst(0−t)0
12
s()t

-TT
ht(