通信系统原理第8章.ppt

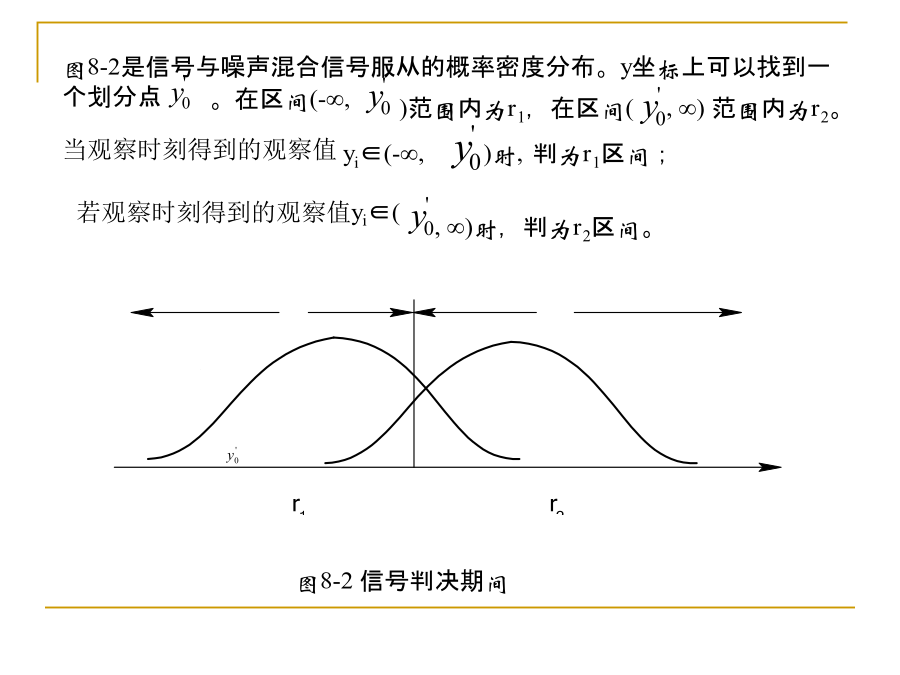
第8章数字信号的最佳接收第8章数字信号的最佳接收8.1引言最佳接收准则2．最大输出信噪比准则-匹配滤波器
在抽样时刻，对每个码元作判决，信噪比越大越好。信噪比越大，误码率就越小。因此，假设存在某种接收方法，使抽样判决时刻的信噪比达到最大，则误码率就会达到最小，这就最大输出信噪比准则。即
和8.2最小差错率准则图8-2信号判决期间如果发送的是s1(t)，但是观察时刻得到的观察值yi却落在r2区间，这时将造成错误判决，因此，发s1(t)而误判为s2(t)的错误概率为在先验概率和似然函数一定的条件下，系统总的误码率Pe是划分点的函数。不同的将有不同的Pe，我们希望选择一个划分点当s1(t)和s2(t)的发送概率相等时，即P(s1)=P(s2)时，则
设信号的持续时间为Ts，在(0,Ts)时间内观测噪声，第i次抽样其概率密度为
根据帕塞瓦尔定理，当k很大时有
8.3确知信号的最佳接收机-理想接收机8.3.1二进制确知信号最佳接收机结构根据上面的分析可知，在加性高斯白噪声条件下，最小差错概率准则与似然比准则是等价的。可以直接利用似然比准则对确知信号做出判决。在观察时间(0，T)内，接收机输入端的信号为s1(t)和s2(t)，信号与噪声的混合波形为
根据式（8-10）判决规则，似然比为式中，P(s1)和P(s2)分别为发送s1(t)和s2(t)的先验概率。对式（8-23）和式（8-24）两边取对数，得根据判决规则，把表达式(8-27)与式（8-28）用框图表示，可得到最佳接收机的模型，如图8-4所示。其中比较器是比较抽样时刻t=T时上下两个支路样值的大小。这种最佳接收机的结构充分考虑了K1和K2对判决的影响，特别是当发送s1(t)的概率为0时，即P(s1)=0，则lnP(s1)=-∞，即K1=-∞，这时式（8-28）总是成立，从而总是判决为s2(t)出现，这个结果正是我们希望的，因为发端只发送了s2(t)。反过来，当P(s2)=0时，情况正好相反。把这种接收机叫做理想接收机。如果发送信号s1(t)和s2(t)的出现概率相等，即P(s1)=P(s2)，可得K1=K2。此时，图中的两个相加器可以省去，则先验等概率情况下的二进制确知信号最佳接收机简化结构为图8-5所示，这个结构属于相关接收机。在后面的章节会介绍，相关接收机的结构来自最小均方误差准则的推导。其中，n(t)是高斯白噪声，其均值为零，方差为若根据式（8-27）进行判决，即再将式（8-29）和式（8-30）代入式（8-33）中，并利用式（8-19），即s1(t)和s2(t)能量相等的条件，可得：根据假设条件，n(t)是高斯随机过程，其均值为零，方差为。根据随机过程理论，高斯型随机变量的线性组合仍然服从高斯分布，而积分运算是线性运算，因此ξ是高斯型随机变量。一个高斯型随机变量被数学期望和方差唯一确定。所以，对于高斯随机变量ξ，只要求出ξ的数学期望和方差，就可以得到ξ的概率密度函数。
ξ的数学期望为至此，可以计算出发送s1(t)时，错误判决为s2(t)的概率为最佳接收机的误码性能与先验概率P(s1)和P(s2)、噪声功率谱密度n0及s1(t)和s2(t)的能量之差有关，而与s1(t)和s2(t)本身的具体结构无关。
一般情况下先验概率是不容易确定的，通常选择先验等概率的假设设计最佳接收机。在发送s1(t)和s2(t)的先验概率相等时，误码率Pe还与s1(t)和s2(t)的能量之差有关，如何设计s1(t)和s2(t)使误码率Pe达到最小，是需要解决的另一个问题。8.3.3抗噪声性能影响因素分析若发送信号s1(t)和s2(t)是不等能量信号，如E1=0，E2=Eb，ρ=0，发送信号s1(t)和s2(t)的平均能量为E=Eb/2，在这种情况下，误码率表示式为8.4最大输出信噪比准则-匹配滤波器式中，s(t)为输入数字信号，其频谱函数为S(ω)。n(t)为高斯白噪声，其双边功率谱密度为n0/2。在抽样时刻t0线性滤波器输出信号的瞬时功率与噪声平均功率之比为式中，X(ω)和Y(ω)都是实变量ω的复函数。当且仅当
根据帕塞瓦尔定理,有8.4.1匹配滤波器的冲击响应匹配滤波器的冲激响应h(t)是输入信号s(t)的镜像函数，t0为输出最大信噪比时刻。对于因果系统，匹配滤波器的冲激响应h(t)应满足8.4.2匹配滤波器的实现1.LC谐振式动态滤波器2.计算法实现动态滤波器3.数字滤波式动态滤波器8.5最小均方误差准则-相关接收机因此，判决规则为
注意，利用E1=E2，整理得：
8.6随相信号的最佳接收机式中
令随机变量为图8-13二进制随相信号最佳接收机结构8.7随机振幅和相位信号的最佳接收8.8最佳基带传输系统8.8.1理想信道下的最佳基带传输系统8.8.2非理想信道下的最佳基带系统8.9*最佳接收