
数字通信原理第11章_伪随机序列及编码.pdf

qw****27








亲,该文档总共41页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

数字通信原理第11章_伪随机序列及编码.pdf
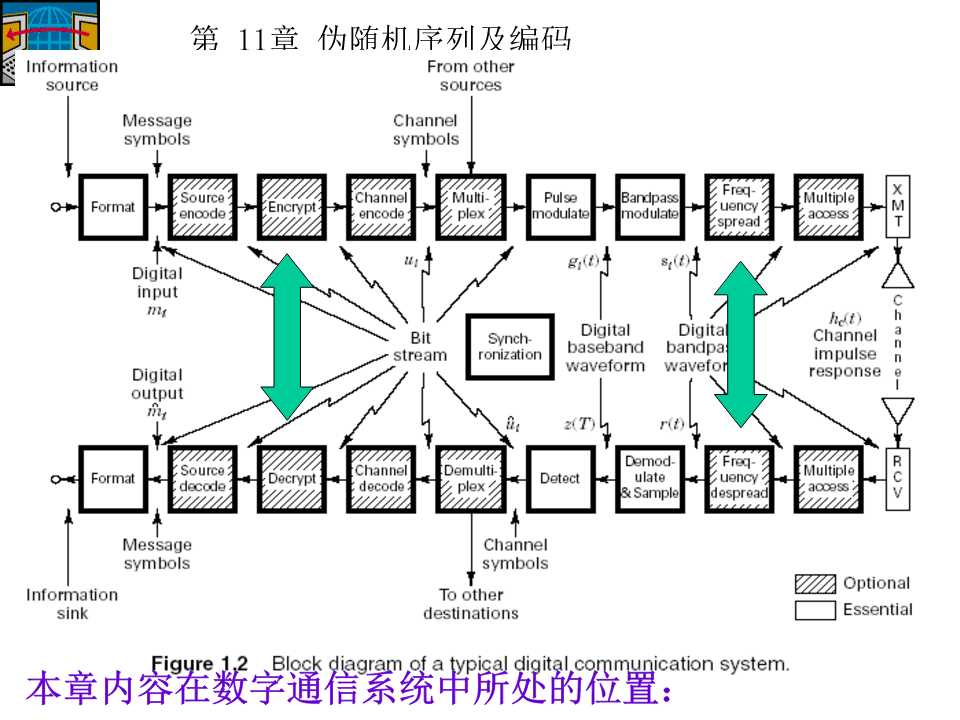
第11章伪随机序列及编码第11章伪随机序列及应用11.1伪随机序列的概念11.2正交码和伪随机码11.3伪随机序列的产生11.4m序列11.5伪随机序列的应用第11章伪随机序列及编码11.1伪随机序列的概念11.1.1基本概念确定序列:可以预先确定且能重复实现的序列。随机序列:既不能预先确定也不能重复实现的序列,性能与噪声性能类似(噪声序列)。伪随机序列:貌似随机序列的确定序列(伪随机码、伪噪声序列、PN码)作用:误码率的测量、通信加密、数据序列的扰码和解码、扩频通信等。第11章伪随机序列及编码伪随机序列

伪随机序列及编码.ppt
指导教师:杨建国二零零七年十一月第十一章伪随机序列及其编码11.1伪随机序列的概念伪随机序列应当具有类似随机序列的性质。在工程上常用二元{0,1}序列来产生伪噪声码,它具有以下几个特点:(1)在随机序列的每一个周期内0和1出现的次数近似相等。(2)每一周期内,长度为n的游程取值(相同码元的码元串)出现的次数比长度为n+1的游程次数多一倍。(3)随机序列的自相关类似于白噪声自相关函数的性质。11.2正交码与伪随机码式中,xi,yi∈(+1,-1),i=1,2,…,n,则x和y之间的互相关函数定义为类似地,

数字通信原理与技术伪随机序列学习教案.pptx
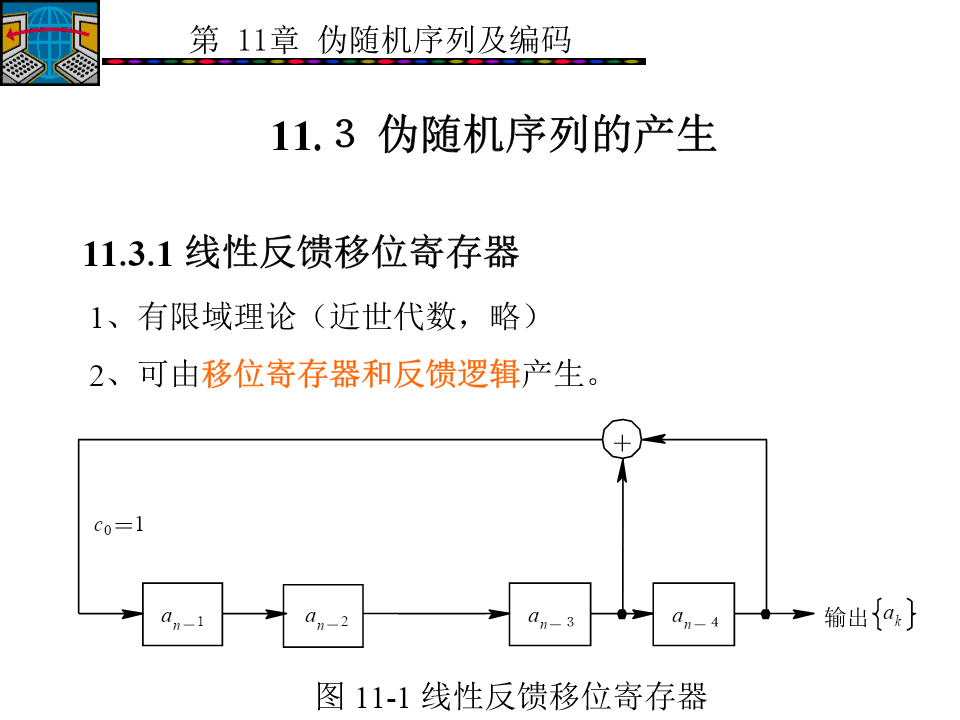
会计学8.1m序列的产生由于带有反馈,因此在移位脉冲作用下,移位寄存器各级的状态将不断变化,通常移位寄存器的最后一级做输出,输出序列为1.线性反馈移位寄存器的递推关系式递推关系式又称为反馈逻辑函数或递推方程。设图8-1所示的线性反馈移位寄存器的初始状态为(a0a1…an-2an-1),经一次移位线性反馈,移位寄存器左端第一级的输入为2.线性反馈移位寄存器的特征多项式用多项式f(x)来描述线性反馈移位寄存器的反馈连接状态:8.1.2m序列产生器图8-2m序列产生器8.2.1均衡特性(平衡性)8.2.2游
伪随机序列.ppt
10.1m序列的产生由于带有反馈,因此在移位脉冲作用下,移位寄存器各级的状态将不断变化,通常移位寄存器的最后一级做输出,输出序列为1.线性反馈移位寄存器的递推关系式递推关系式又称为反馈逻辑函数或递推方程。设图10-1所示的线性反馈移位寄存器的初始状态为(a0a1…an-2an-1),经一次移位线性反馈,移位寄存器左端第一级的输入为2.线性反馈移位寄存器的特征多项式用多项式f(x)来描述线性反馈移位寄存器的反馈连接状态:10.1.2m序列产生器图10-2m序列产生器10.2.1均衡特性(平衡性)10.2

伪随机序列及其应用.pdf
