
定积分的概念和性质.ppt

天马****23





亲,该文档总共23页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

定积分的概念和性质.ppt
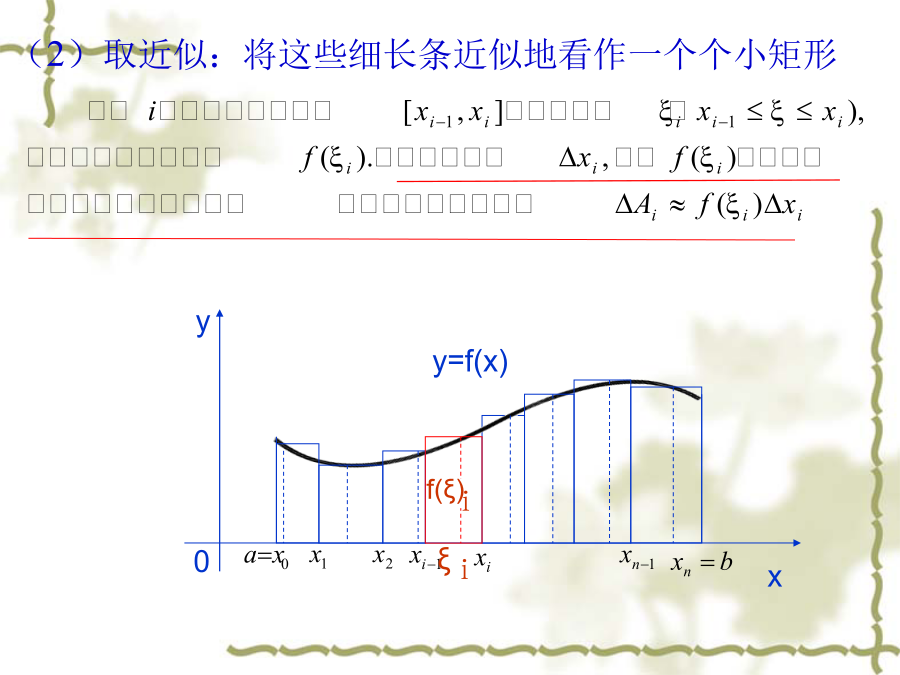
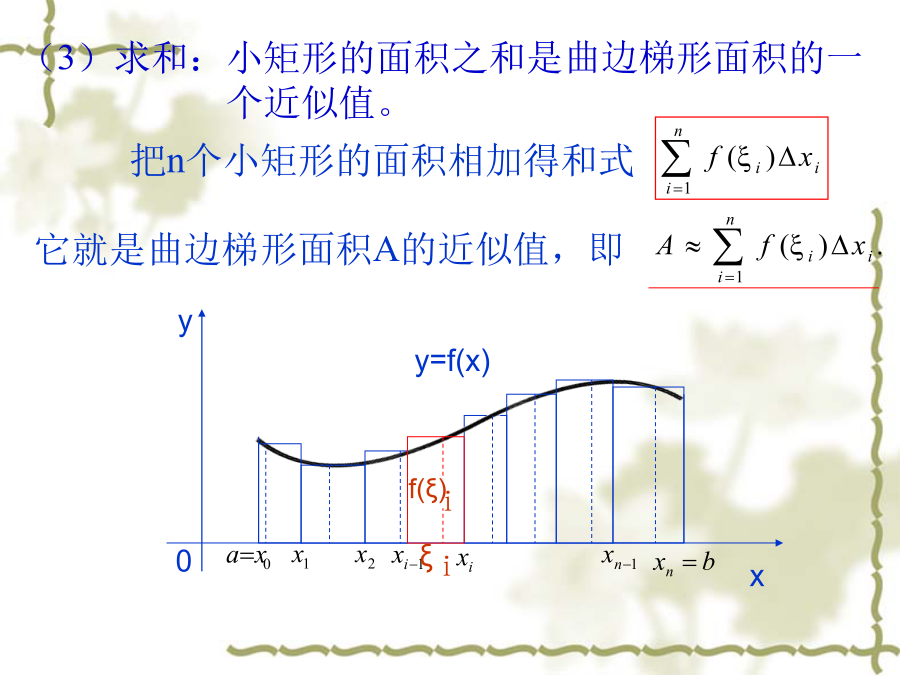
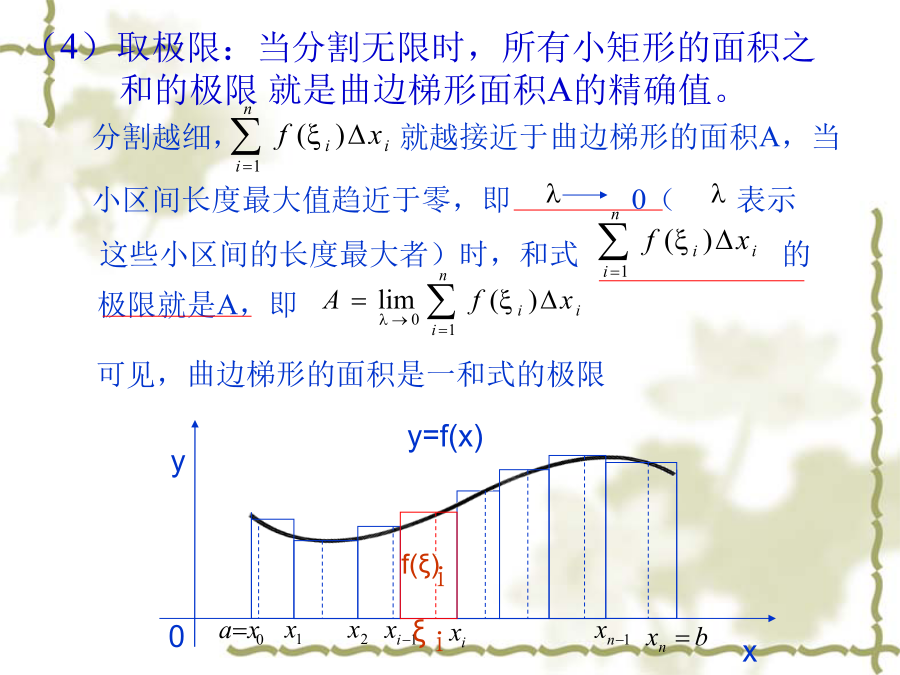
定积分概念思想方法(2)取近似:将这些细长条近似地看作一个个小矩形(3)求和:小矩形的面积之和是曲边梯形面积的一个近似值。(4)取极限:当分割无限时,所有小矩形的面积之和的极限就是曲边梯形面积A的精确值。2、变速直线运动的路程设某物体作直线运动,已知速度是时间间隔上t的连续函数,且,计算在此段时间内物体经过的路程。(2)近似求和:二、定积分的定义定义设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点:分划任取,作和式近似求和记,如果取极限存在,且极限值I不依赖于的选取,也不依赖于[a,b]

定积分的概念和性质.docx
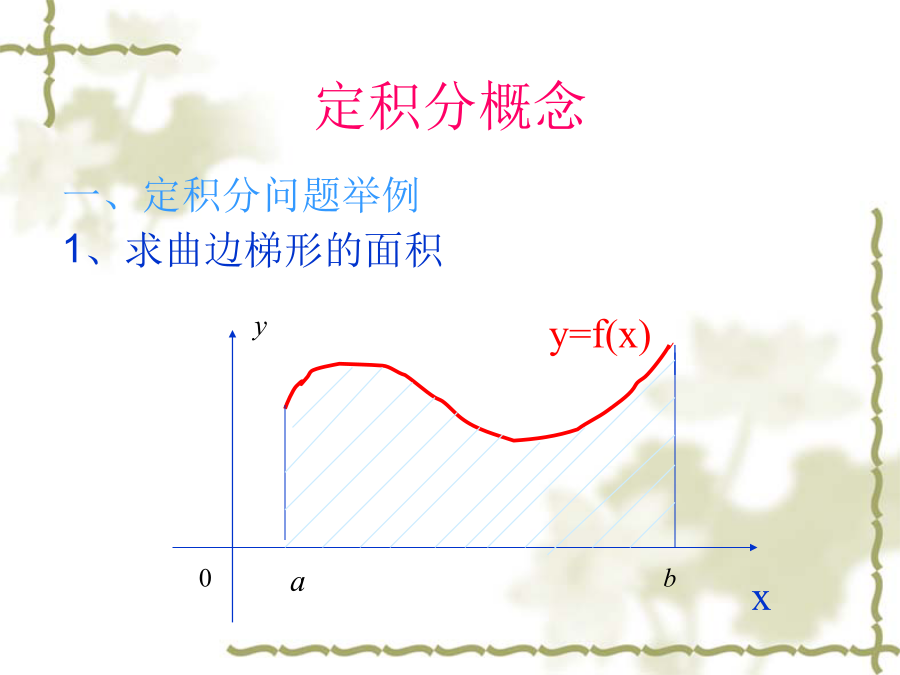
第五章定积分Chapter5DefiniteIntegrals5.1定积分的概念和性质(ConceptofDefiniteIntegralanditsProperties)一、定积分问题举例(ExamplesofDefiniteIntegral)设在区间上非负、连续,由,,以及曲线所围成的图形称为曲边梯形,其中曲线弧称为曲边。Letbecontinuousandnonnegativeontheclosedinterval.Thentheregionboundedbythegraphof,the-axis,

定积分的概念和性质公式.pdf
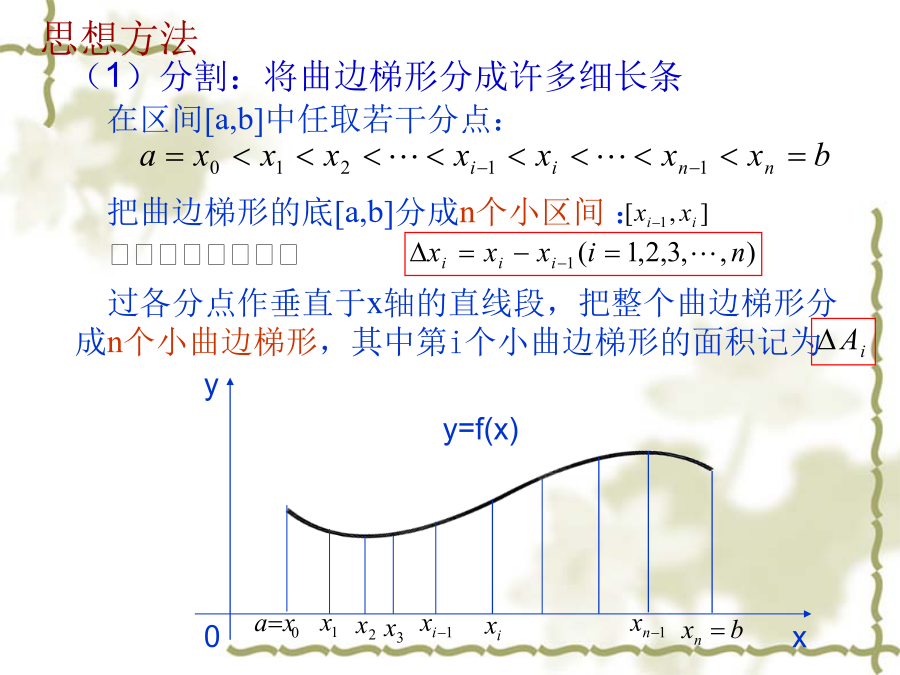
.1.曲边梯形的面积设在区间上,则由直线、、及曲线所围成的图形称为曲边梯形,下面求这个曲边梯形的面积分割求近似:在区间中任意插入若干个分点将分成n个小区间,小区间的长度在每个小区间上任取一点作乘积,求和取极限:则面积取极限..其中,即小区间长度最大者趋于零。2.变速直线运动的路程设某物体作变速直线运动,速度是上的连续函数,且,求在这段时间内物体所经过的路程。分割求近似:在内插入若干分点将其分成n个小区间,小区间长度,。任取,做求和取极限:则路程取极限定义设函数在上有界,在中任意插入若干个分点将分成n个小区

定积分的概念和性质公式.doc
DDY整理1.曲边梯形的面积设在区间上,则由直线、、及曲线所围成的图形称为曲边梯形,下面求这个曲边梯形的面积分割求近似:在区间中任意插入若干个分点将分成n个小区间,小区间的长度在每个小区间上任取一点作乘积,求和取极限:则面积取极限其中,即小区间长度最大者趋于零。2.变速直线运动的路程设某物体作变速直线运动,速度是上的连续函数,且,求在这段时间内物体所经过的路程。分割求近似:在内插入若干分点将其分成n个小区间,小区间长度,。任取,做求和取极限:则路程取极限定义设函数在上有界,在中任意插入若干个分点将分成n个

定积分的概念和性质公式.doc
1.曲边梯形的面积设在区间上,则由直线、、及曲线所围成的图形称为曲边梯形,下面求这个曲边梯形的面积分割求近似:在区间中任意插入若干个分点将分成n个小区间,小区间的长度在每个小区间上任取一点作乘积,求和取极限:则面积取极限其中,即小区间长度最大者趋于零。2.变速直线运动的路程设某物体作变速直线运动,速度是上的连续函数,且,求在这段时间内物体所经过的路程。分割求近似:在内插入若干分点将其分成n个小区间,小区间长度,。任取,做求和取极限:则路程取极限定义设函数在上有界,在中任意插入若干个分点将分成n个小区间,其
