
椭偏测薄膜厚度.ppt

天马****23









亲,该文档总共27页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

椭偏测薄膜厚度.ppt
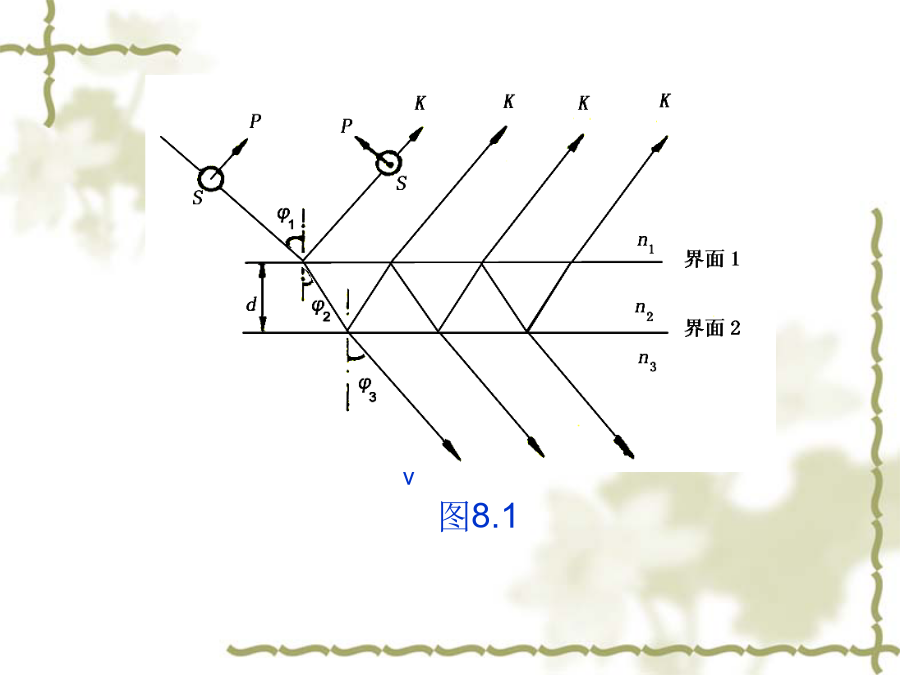
【实验目的】【实验原理】图8.1设表示光的入射角,和分别为在界面1和2上的折射角.根据折射定律有(8.1)光波的电矢量可以分解成在入射面内振动的p分量和垂直于入射面振动的s分量.若用Eip和Eis分别代表入射光的p和s分量,用Erp及Ers分别代表各束反射光K0,K1,K2,…中电矢量的p分量之和及s分量之和,则膜对两个分量的总反射系数Rp和Rs定义为(8.2)经计算可得(8.3)式中,r1p或r1s和r2p或r2s分别为p或s分量在界面1和界面2上一次反射的反射系数。为任意相邻两束反射光之间的位相差。根

椭偏测薄膜厚度.ppt
【实验目的】【实验原理】图8.1设表示光的入射角,和分别为在界面1和2上的折射角.根据折射定律有(8.1)光波的电矢量可以分解成在入射面内振动的p分量和垂直于入射面振动的s分量.若用Eip和Eis分别代表入射光的p和s分量,用Erp及Ers分别代表各束反射光K0,K1,K2,…中电矢量的p分量之和及s分量之和,则膜对两个分量的总反射系数Rp和Rs定义为(8.2)经计算可得(8.3)式中,r1p或r1s和r2p或r2s分别为p或s分量在界面1和界面2上一次反射的反射系数。为任意相邻两束反射光之间的位相差。根

椭偏测薄膜厚度.ppt
用椭圆偏振仪测量薄膜厚度——叶昕【实验目的】【实验原理】图8.1设表示光的入射角,和分别为在界面1和2上的折射角.根据折射定律有(8.1)光波的电矢量可以分解成在入射面内振动的p分量和垂直于入射面振动的s分量.若用Eip和Eis分别代表入射光的p和s分量,用Erp及Ers分别代表各束反射光K0,K1,K2,…中电矢量的p分量之和及s分量之和,则膜对两个分量的总反射系数Rp和Rs定义为(8.2)经计算可得(8.3)式中,r1p或r1s和r2p或r2s分别为p或s分量在界面1和界面2上一次反射的反射系数。为任

基于穆勒椭偏的纳米薄膜厚度测量与溯源.pptx
汇报人:目录PARTONEPARTTWO穆勒椭偏法的定义椭偏参数与薄膜厚度的关系测量原理的数学模型PARTTHREE穆勒椭偏仪:用于测量纳米薄膜厚度光学显微镜:用于观察纳米薄膜表面形貌电子显微镜:用于观察纳米薄膜内部结构热蒸发仪:用于制备纳米薄膜激光干涉仪:用于测量纳米薄膜厚度电子束蒸发仪:用于制备纳米薄膜扫描电子显微镜:用于观察纳米薄膜表面形貌和内部结构光学椭偏仪:用于测量纳米薄膜厚度电子束蒸发仪:用于制备纳米薄膜扫描电子显微镜:用于观察纳米薄膜表面形貌和内部结构光学椭偏仪:用于测量纳米薄膜厚度电子束蒸

椭偏测薄膜厚学习教案.pptx
会计学【实验(shíyàn)原理】图8.1设表示光的入射角,和分别为在界面1和2上的折射角.根据(gēnjù)折射定律有(8.1)光波的电矢量可以分解成在入射面内振动的p分量和垂直于入射面振动的s分量.若用Eip和Eis分别代表入射光的p和s分量,用Erp及Ers分别代表各束反射光K0,K1,K2,…中电矢量的p分量之和及s分量之和,则膜对两个分量的总反射系数Rp和Rs定义为(8.2)经计算可得(8.3)式中,r1p或r1s和r2p或r2s分别为p或s分量在界面1和界面2上一次反射的反射系数。为任意相邻两
