
1复数及复变函数.ppt

雨巷****碧易






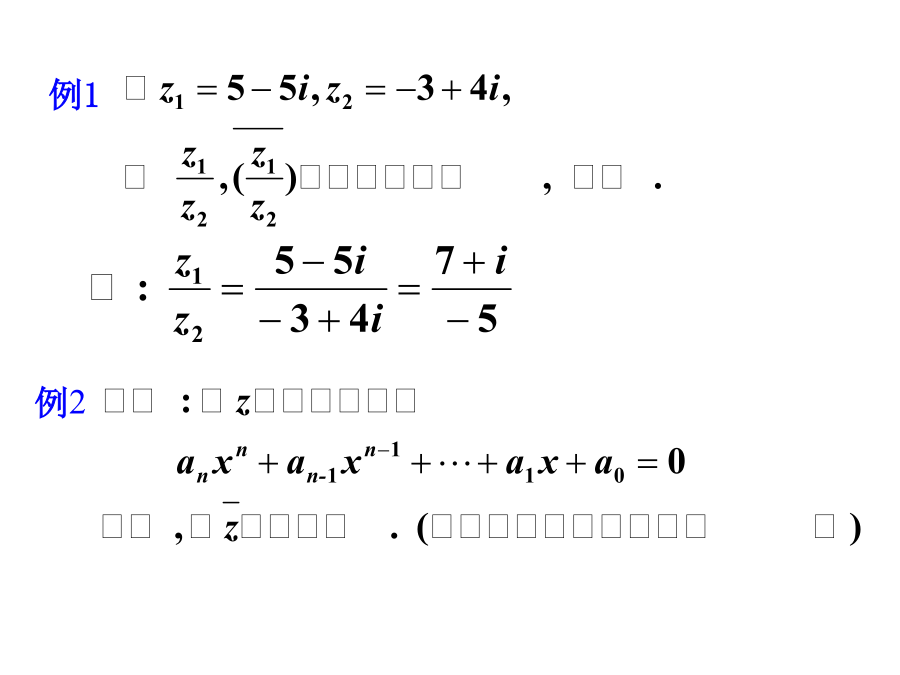



亲,该文档总共58页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

复变函数复数与复变函数.pptx
第一章复数与复变函数复变函数与积分变换及应用背景的概念,从而建立了复变函数理论.(4)应用于计算绕流问题中的压力和力矩等.变换应用于频谱分析和信号处理等.变换应用于控制问题.主要内容§1.1复数1.1.1复数的概念显然,z=x+iy是x-iy的共轭复数,即1.1.2复数的四则运算(3)复数的商3.分配律解:例1.2给定一复数z=x+iy,在坐标平面XOY上存在惟一的点P(x,y)与z=x+iy对应.反之,对XOY平面上的点P(x,y),存在惟一的复数z=x+iy与它对应.根据复数的代数运算及向量的代数运算

复数与复变函数题库_复数和复变函数.docx
复数与复变函数题库_复数和复变函数一.复数与复变函数㈠选择1.包含了单位圆盘|z|B.-π4C.π4D.3π43.复数方程z=3t+it表示的曲线是()A.直线B.圆周C.椭圆D.双曲线4.设z=x+iy,则|e2i+2z|=()A.e2+2xB.e|2i+2z|C.e2+2zD.e2x5.下列集合为无界多连通区域的是()A.0πC.|z+ie|>4D.32πi的辐角为()A.arctan1B.-arctan12C.π-arctan12D.π+arctan1227.方程Rez2=1所表示的平面曲线为()A

1复数及复变函数.ppt
CH1复数及复变函数1.复数的概念一般任意两个复数不能比较大小.定义z1=x1+iy1与z2=x2+iy2的和、差、积和商为:z1±z2=(x1±x2)+i(y1±y2)z1z2=(x1+iy1)(x2+iy2)=(x1x2-y1y2)+i(x2y1+x1y2)z1+z2=z2+z1;z1z2=z2z1;(z1+z2)+z3=z1+(z2+z3);z1(z2z3)=(z1z2)z3;z1(z2+z3)=z1z2+z1z3.例11.代数形式1.代数形式(点表示)2.几何形式(向量表示)辐角无穷多:Argz=

1复数及复变函数.ppt
CH1复数及复变函数1.复数的概念一般任意两个复数不能比较大小.定义z1=x1+iy1与z2=x2+iy2的和、差、积和商为:z1±z2=(x1±x2)+i(y1±y2)z1z2=(x1+iy1)(x2+iy2)=(x1x2-y1y2)+i(x2y1+x1y2)z1+z2=z2+z1;z1z2=z2z1;(z1+z2)+z3=z1+(z2+z3);z1(z2z3)=(z1z2)z3;z1(z2+z3)=z1z2+z1z3.例11.代数形式1.代数形式(点表示)2.几何形式(向量表示)辐角无穷多:Argz=

1复数及复变函数.ppt
CH1复数及复变函数1.复数的概念一般任意两个复数不能比较大小.定义z1=x1+iy1与z2=x2+iy2的和、差、积和商为:z1±z2=(x1±x2)+i(y1±y2)z1z2=(x1+iy1)(x2+iy2)=(x1x2-y1y2)+i(x2y1+x1y2)z1+z2=z2+z1;z1z2=z2z1;(z1+z2)+z3=z1+(z2+z3);z1(z2z3)=(z1z2)z3;z1(z2+z3)=z1z2+z1z3.例11.代数形式1.代数形式(点表示)2.几何形式(向量表示)辐角无穷多:Argz=
