预览加载中，请您耐心等待几秒...

条件分布律条件分布函数条件概率密度.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共37页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

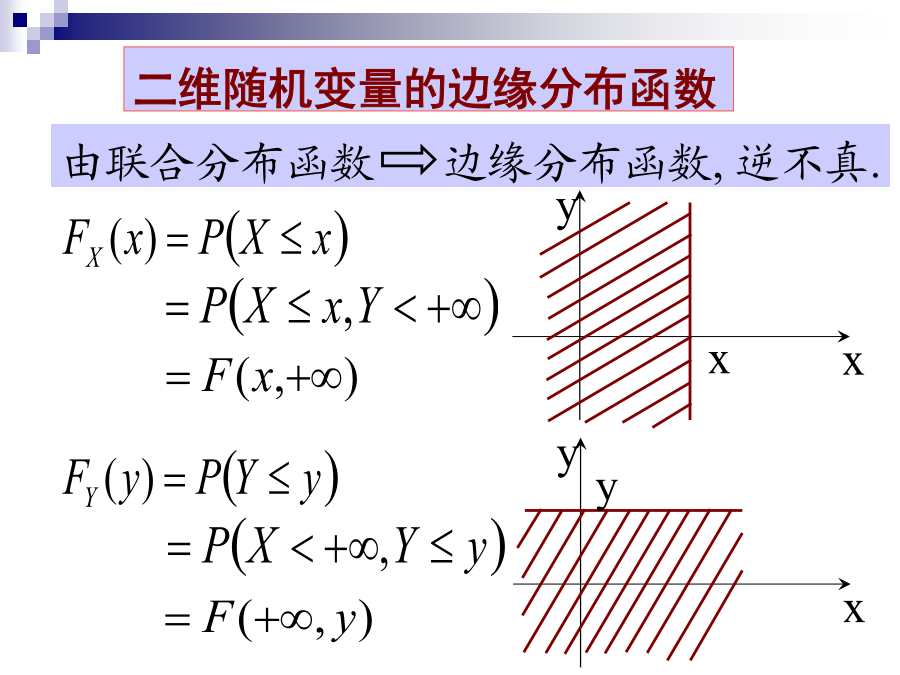
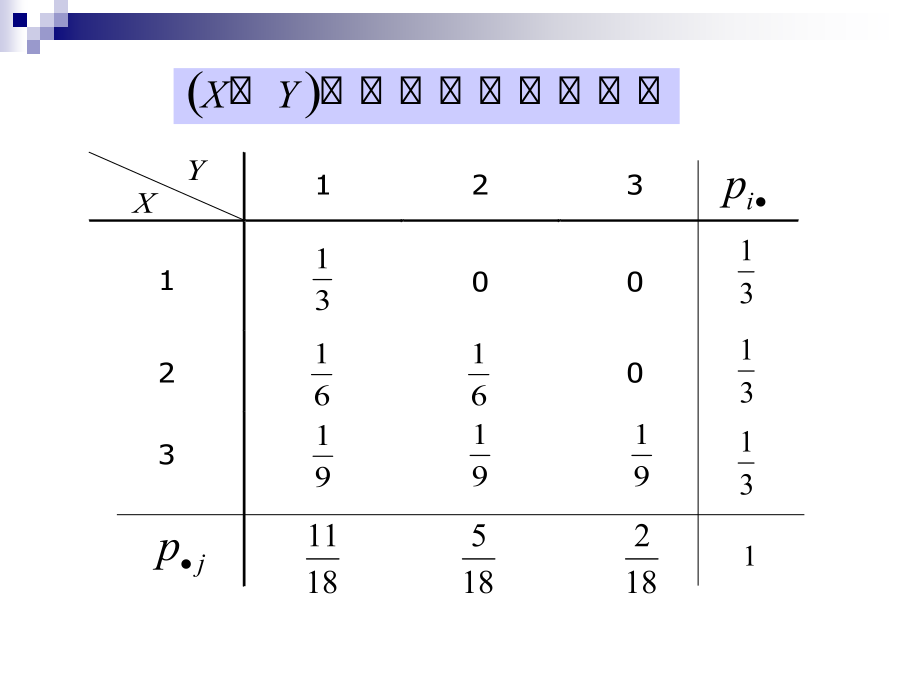
二维随机变量的边缘分布函数例设随机变量(X,Y)的联合分布函数为解(1)(3)二维离散型随机变量的边缘分布1例(P55.1)设随机变量X在1,2,3三个数中等可能地取值，另一个随机变量Y在1~X中等可能地取一整数值，试求X,Y的边缘分布律。例箱子里装有4只白球和2只黑球，在其中随 机地取两次，每次取一只。考虑两种试验： （1）有放回抽样，（2）不放回抽样。 我们定义随机变量X，Y如下，写出X和Y的联 合分布律和边缘分布律。（1）有放回抽样（2）不放回抽样已知联合密度可以求得边缘密度yy例结论（一）条件分布律 条件分布函数 条件概率密度在第一章中，我们介绍了条件概率的概念.一.离散型随机变量的条件分布律由条件概率公式自然地引出如下定义：例(P55.1)设随机变量X在1,2,3三个数中等可能地取值，另一个随机变量Y在1~X中等可能地取一整数值，求Y=1时，X的条件分布律。X二.连续型随机变量的条件分布定义：给定y，设对于任意固定的正数， P(y-<Yy+)>0,若对于任意实数x，由条件分布函数可以引出条件概率密度在条件Y=y下X的条件分布函数定义例已知同理，例设y=x例已知解