线性规划求最优解.ppt

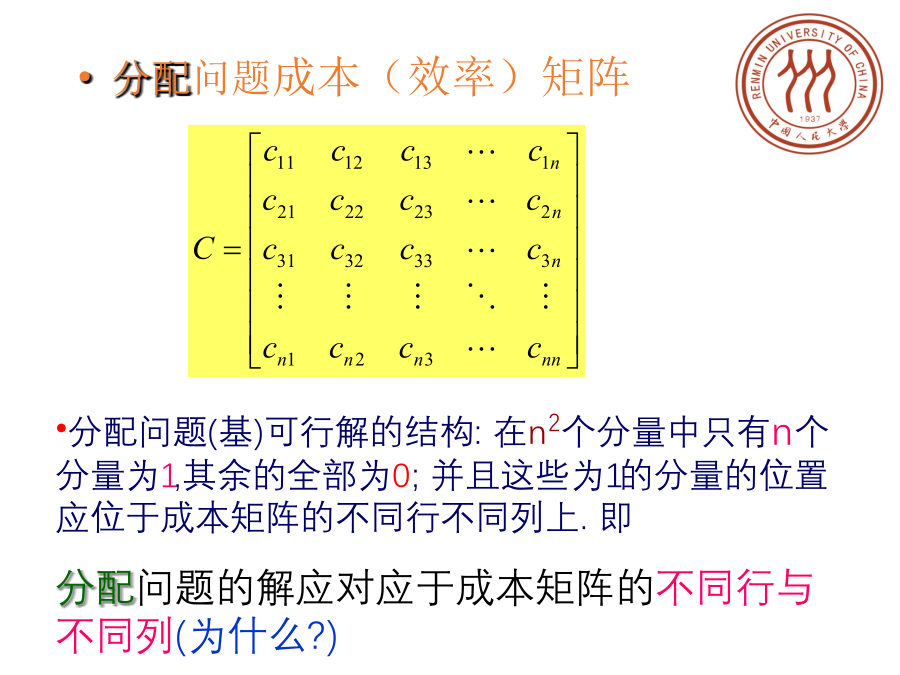
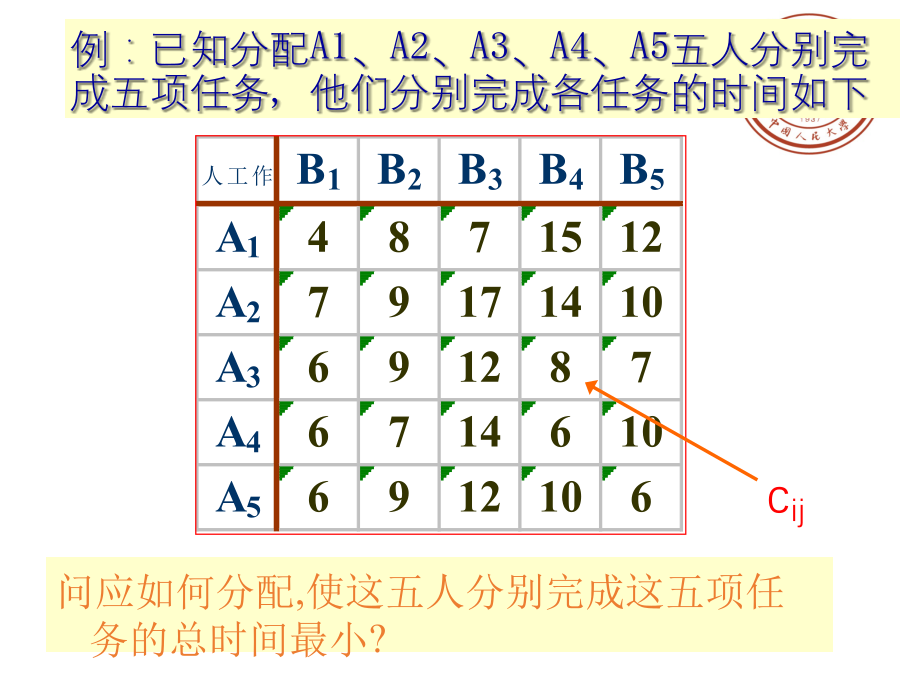
1第二节经典分配(指派)问题与匈牙利法分配问题的数学模型设决策变量为：4例：已知分配A1、A2、A3、A4、A5五人分别完成五项任务,他们分别完成各任务的时间如下匈牙利算法基本思想分配问题的性质—匈牙利算法的依据8指派问题的性质(续)分配问题的求解-匈牙利方法步骤覆盖原则变换原则例题求解14一般指派问题最大化分配问题最大化分配问题人数和工作数不等的分配问题一个人可做几项工作的分配问题某项工作一定不能由某人做的分配问题21222324目标规划
(Goalprogramming)目标规划是在线性规划的基础上，为适应经济管理中多目标决策的需要而逐步发展起来的一个分支。4、线性规划的最优解是绝对意义下的最优，但需花去大量的人力、物力、财力才能得到；实际过程中，只要求得满意解，就能满足需要（或更能满足需要）。（二）、目标规划的基本概念产品Ⅰ产量不大于产品Ⅱ。
超过计划供应原材料时，需高价采购，这使成本增加。
应尽可能充分利用设备工时，但不希望加班。
利润不少于56元。
用式子表示：
x1-x2≤0
2x1+x2≤11
x1+2x2=10
8x1+10x2≥56
左边：决策值（表示实际执行效果）
右边：目标值（表示理想目标）
实际效果与理想目标之间可能有偏差值（不足或者超过），若引入偏差变量，就可变成等式。
例题4—2：
解：确定优先因子后得数学模型：
minZ=P1d1++P2(d2-+d2+)+P3d3-
2x1+x2≤11（在绝对约束基础上进行目标规划）
x1-x2+d1--d1+=0
(要求：d1+尽可能小，最好是0才能满足≤)
x1+2x2+d2--d2+=10
（要求：d2-和d2+都尽可能小，最好等于0）
8x1+10x2+d3--d3+=56
（要求：d3-尽可能小，最好是0才能满足≥）
x1,x2,di-,di+≥0