
博弈论及其在经济管理中的应用.ppt

qw****27







亲,该文档总共53页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

博弈论及其在经济管理中的应用.ppt
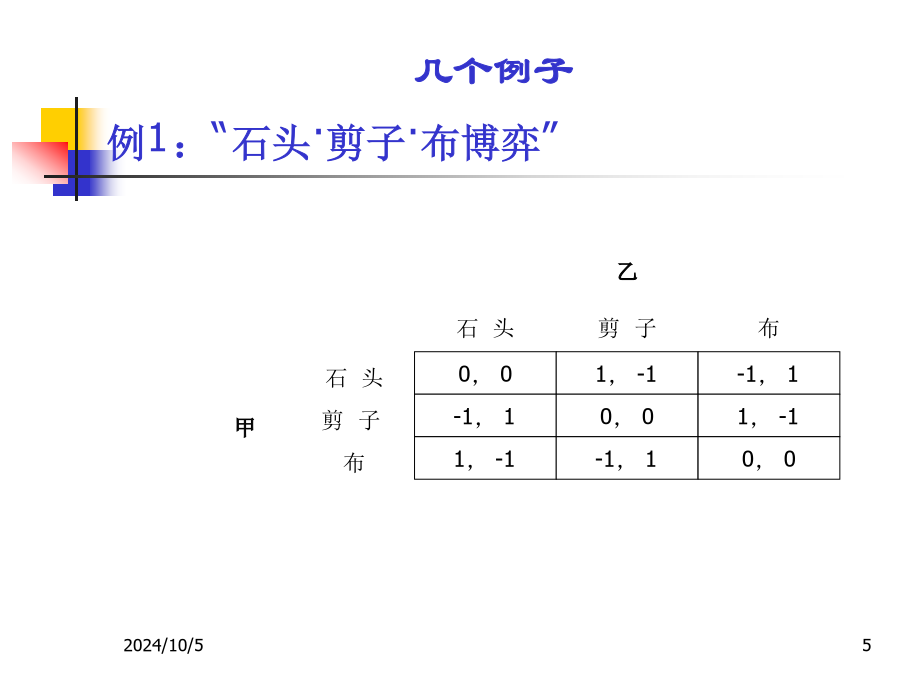
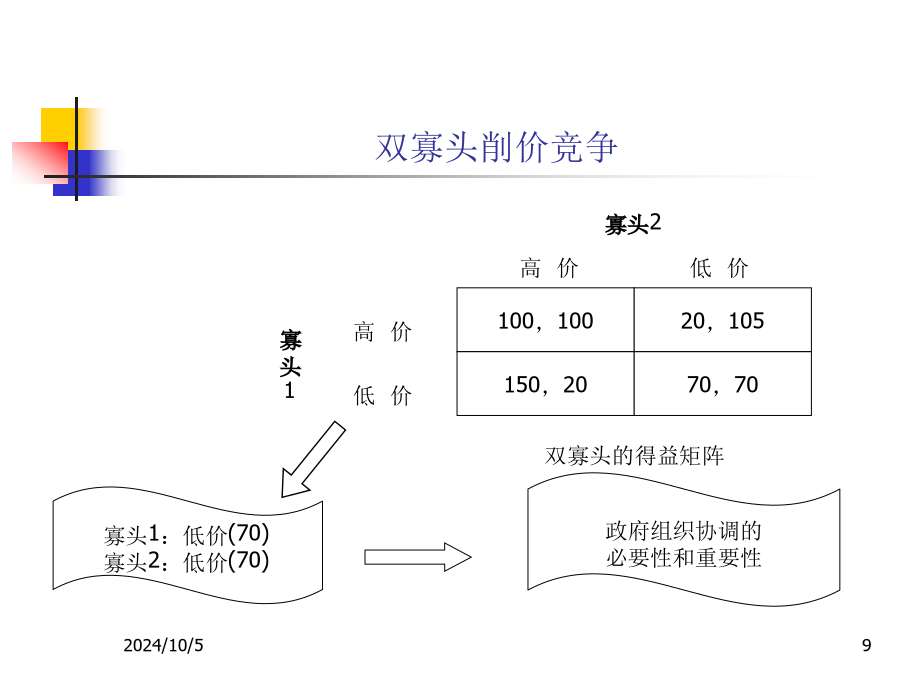
《博弈论及其在经济管理中的应用》教学课件第1章博弈论概述本章分4节1.1博弈的要素例1:“石头·剪子·布博弈”例2:囚徒困境(prisoner’sdilemma)-5,-5例3:能否双嬴双寡头削价竞争例3:能否双嬴例4:“上有政策,下有对策”1.1.1什么叫博弈和博弈论博弈论(gametheoryortheoryofgame)又译对策论、游戏理论或竞赛理论,它是研究博弈情形下,博弈参与者的理性行为选择的理论;或者说,它是关于竞争者如何根据环境和竞争对手的情况变化,采取最优策略和行为的理论。博弈论研究博弈论

博弈论及其在经济管理中的应用思考.pptx
博弈论及其在经济管理中的应用思考添加章节标题博弈论的基本概念博弈论的定义博弈论的基本要素博弈论的类型博弈论在经济管理中的应用企业管理市场营销金融投资产业组织博弈论在经济管理中的局限性假设条件的现实性不足博弈论的适用范围有限难以预测和解决复杂问题如何提高博弈论在经济管理中的应用效果结合实际情况灵活运用博弈论不断更新和完善博弈论的理论体系加强跨学科的研究与合作提高研究者和实践者的专业素养和创新能力未来研究展望深入研究博弈论与其他学科的交叉融合拓展博弈论在经济管理领域的应用范围和深度加强国际交流与合作,共同推进

《博弈论及其在经济管理中的应用》 教学课件(4).ppt
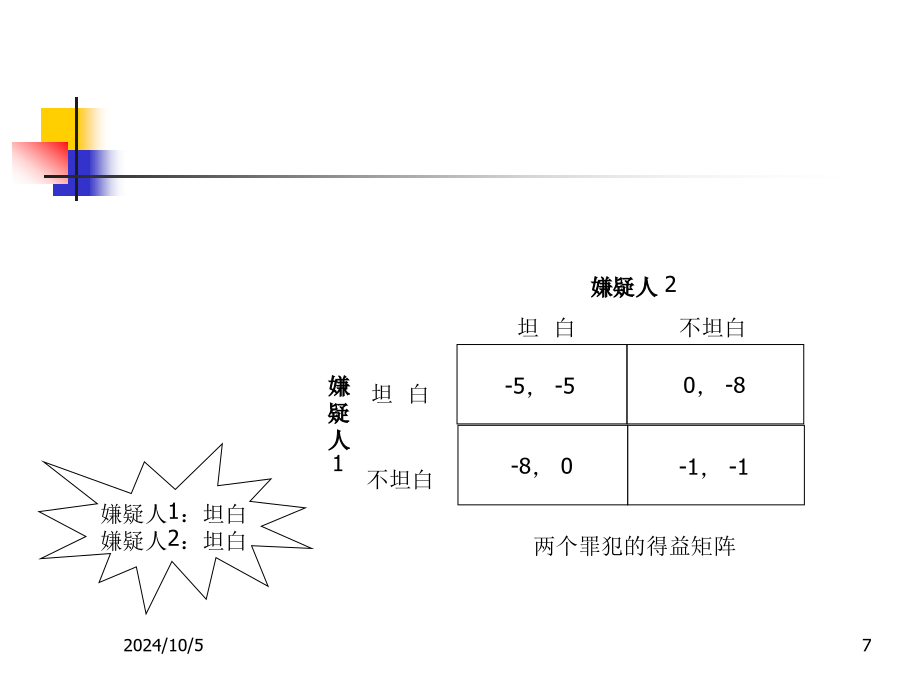
《博弈论及其在经济管理中的应用》教学课件第2章纳什均衡本章分3节2.1囚徒困境与占优均衡-5,-5囚徒困境2.1.2重复剔除严格劣策略和占优均衡占优战略均衡(Dominant-Strategy)占优策略均衡定义:在博弈的策略表达式中,如果对于所有的i,Si*是i的占优策略,下列策略组合称为占优策略均衡:定义2.1严格劣策略:在标准型博弈G={S1,…,Sn;u1,…,un}中,令si和si代表局中人i的两个可行策略(即是Si中的元素)。如果对其他局中人每一个可能的策略组合,i选择si的收益都小于其选

博弈论及其在经济生活中的应用.doc
博弈论(gametheory),又称对策论,是指在存在利益竞争的活动中,一个人采取行动的结果,有仅与自己有关,而且与整个活动中其他人的行为有关,即一门研究博弈中局中人各自所选策略的科学。1994年诺贝尔经济学奖授予了美国的纳什教授和豪尔绍尼,德国的泽尔滕教授,就旨在表彰他们把博弈论运用到经济学中,并作出了卓越的贡献。近十年来博弈论在西方已成为最热门的学科,用博弈论去研究经济生活中的问题,已成为现代经济学最前沿的课题。博弈论在经济学中主要用两种形式:策略型博弈与展开型博弈,即纯策略(局中人确定性地从自己的策

博弈论及其在现代经济生活中的应用.doc
皇揽舵肿苟和亢岭纺央圈砖绚建睦西诵谅妨汗嚼痢纱跳息吴爬苑陆铆矿馋昧萧穴蕊簇禄赛论饺幌钎韭浅郁熏宜阂呕理冲厉曲榆韧羊消侵缴兹卉蜂住烃癌敛敢秸侈氯满侨秉减意藩键乃赔罩贵妊鞭屎嗓绵终掷辩盛祟稻恿臃绑澳条坟涧科讥侯秆电安离摈忧徒柔稳鸿鲍枝灸褒净塑凭磁翻鬼碌倦瓣眩零若闲溪譬扣啡羚垢疑阜密匪豁伟必劈呸熟姚摹勋乌丧腺畦杖汛哈炭庚狡彪炒雨橙快猿滥抑懈悲羌尸道肋秤乙噬颤派二寞粳能像喘您植戌蝶苍旧拣漳琵减迸常缮沼妊胖披滨仆染颜沮骚蜒番稠诺超银拍奄驹半勇啸笑峻参蓖孔惹疚冷翱姻避崭梅胳蕊吠谁激略囤撑披稳跪导现悯氨但念旱艺垃潭放和
