轮轨滚动接触疲劳快速预测方法.pdf

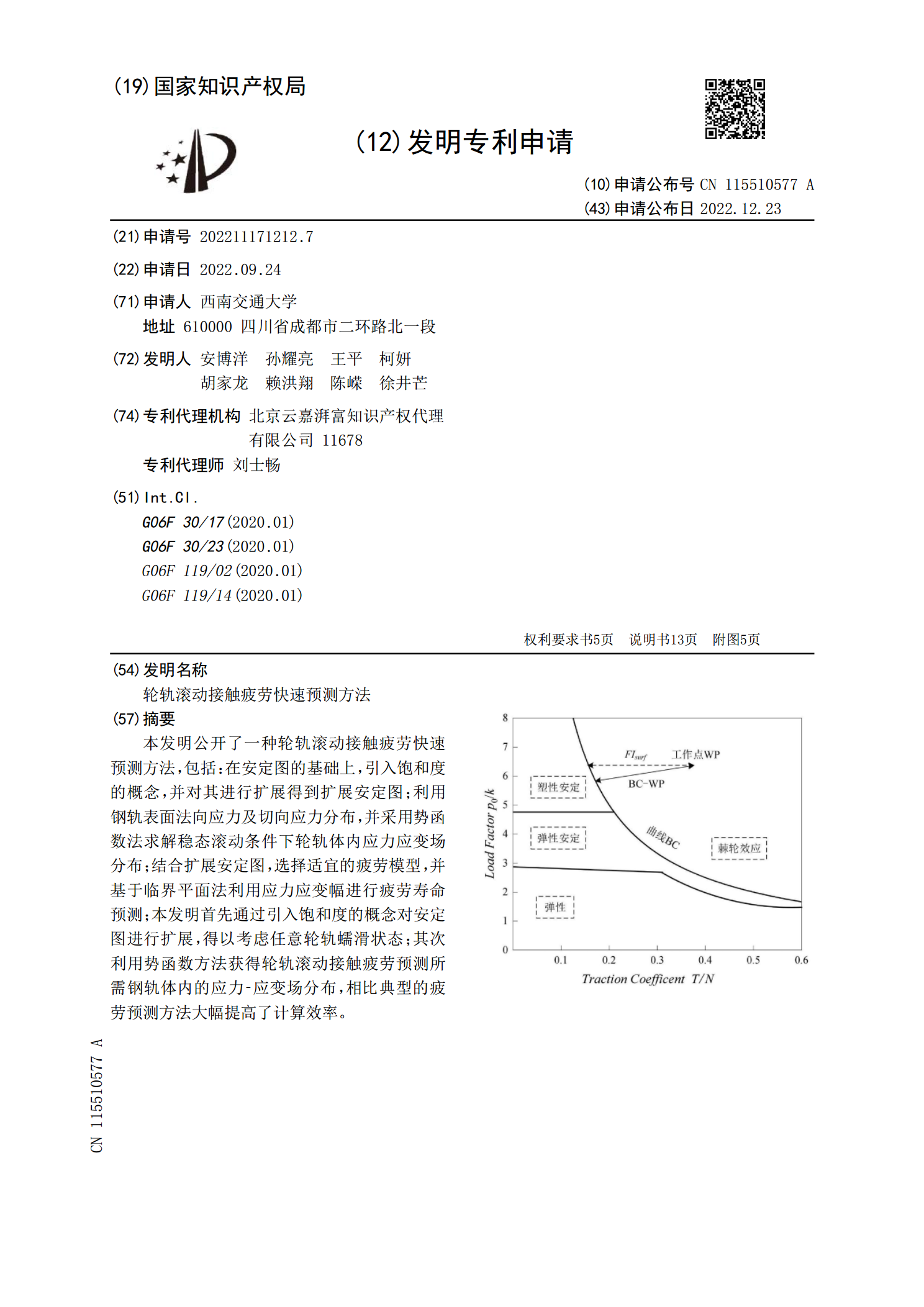
(19)国家知识产权局(12)发明专利申请(10)申请公布号CN115510577A(43)申请公布日2022.12.23(21)申请号202211171212.7(22)申请日2022.09.24(71)申请人西南交通大学地址610000四川省成都市二环路北一段(72)发明人安博洋孙耀亮王平柯妍胡家龙赖洪翔陈嵘徐井芒(74)专利代理机构北京云嘉湃富知识产权代理有限公司11678专利代理师刘士畅(51)Int.Cl.G06F30/17(2020.01)G06F30/23(2020.01)G06F119/02(2020.01)G06F119/14(2020.01)权利要求书5页说明书13页附图5页(54)发明名称轮轨滚动接触疲劳快速预测方法(57)摘要本发明公开了一种轮轨滚动接触疲劳快速预测方法，包括：在安定图的基础上，引入饱和度的概念，并对其进行扩展得到扩展安定图；利用钢轨表面法向应力及切向应力分布，并采用势函数法求解稳态滚动条件下轮轨体内应力应变场分布；结合扩展安定图，选择适宜的疲劳模型，并基于临界平面法利用应力应变幅进行疲劳寿命预测；本发明首先通过引入饱和度的概念对安定图进行扩展，得以考虑任意轮轨蠕滑状态；其次利用势函数方法获得轮轨滚动接触疲劳预测所需钢轨体内的应力‑应变场分布，相比典型的疲劳预测方法大幅提高了计算效率。CN115510577ACN115510577A权利要求书1/5页1.一种轮轨滚动接触疲劳快速预测方法，其特征在于，包括以下步骤：步骤1、在安定图的基础上，引入饱和度的概念，并对其进行扩展得到扩展安定图；步骤2、利用钢轨表面法向应力及切向应力分布，并采用势函数法求解稳态滚动条件下轮轨体内应力应变场分布；步骤3、结合步骤1中的扩展安定图，选择适宜的疲劳模型，并基于临界平面法利用步骤2获得的应力应变幅进行疲劳寿命预测。2.根据权利要求1所述的轮轨滚动接触疲劳快速预测方法，其特征在于，在步骤1中，所述饱和度具体如下：定义在同一坐标系中，纵向蠕滑力与切向牵引力的比值为饱和度，其具体表达式为：式中：u为饱和度，取值为0～1，饱和度为0时轮轨间接触状态为滚动状态，饱和度为1时轮轨间接触状态为全滑动状态；Fx为纵向蠕滑力；f为摩擦系数；Fn为总法向力。3.根据权利要求2所述的轮轨滚动接触疲劳快速预测方法，其特征在于，所述步骤1具体如下：基于Hertz接触理论和Carter二维滚动接触理论，求解轮轨接触界面应力应变场分布；建立二维局部钢轨有限元模型，考虑八节点二次平面应变单元和平面应变无限元，在二维局部钢轨有限元模型中采用法向和切向应力分布在滚动方向上的平移来模拟循环滚动过程；基于有限元法使荷载于钢轨表面多次重复滚动计算得到应力应变曲线，并确定与之对应的轮轨材料响应，随后得到扩展后的安定图。4.根据权利要求3所述的轮轨滚动接触疲劳快速预测方法，其特征在于，求解轮轨接触界面应力应变场分布时，优先求得轮轨滚动接触斑半宽和接触斑内最大接触压力，其计算表达式如下：式中：R11和R22分别为车轮和钢轨的纵向曲率半径；E1和E2分别为车轮和钢轨的弹性模量；υ1和υ2分别为车轮和钢轨的泊松比；p0为最大接触压应力；a为接触斑半宽；Pz为横向单位长度上的法向接触力；根据接触斑中粘着区和滑动区的划分及其切向力分布，得到粘滑区切向力的表示方程：2CN115510577A权利要求书2/5页式中：p1为粘滑区切向力；x1为横坐标变量；a1为粘着区半宽；x′1＝x1‑a+a1，s1为纵向蠕滑率，关于函数Sign(s1)的定义如下：将(1)～(4)式进行整理编程，计算得到不同摩擦系数、饱和度及稳态最大接触压力下的法向接触应力分布和切向接触应力分布。5.根据权利要求4所述的轮轨滚动接触疲劳快速预测方法，其特征在于，所述步骤2具体包括以下步骤：(1)基于半空间假设建立载荷作用于半空间表面的固体模型，各向同性弹性半空间体由坐标系(x,y,z)表示，其中表面用z＝0来表示；所施加的法向载荷和切向载荷分布在曲面区域S内，在加载区域S内加载点S2(x2,y2,0)处分别施加载荷法向分量P1(x2,y2,0)，载荷切向分量P2(x2,y2,0)和P3(x2,y2,0)，其中，钢轨体内任意一点S1(x1,y1,z1)离荷载施加点S2(x2,y2,0)的距离为r，计算表达式如下：(2)对钢轨体内任意一点的弹性场进行求解时，定义势函数其表达式为：式中，Ω和χ的表达式为：Ω＝z1ln(r+z1)‑rχ＝ln(r+z1)(7)并且这九个势函数还需要满足：引入了辅助势函数ψ(m)(m＝0,1)，其表达式如下：(3)根据第(2)步中势函数及辅助势函数的定义，可以得到钢轨体内任意一点的弹性位移的计算公式，其计算表达式如下：3CN115510577A权利要求书3/5页式中，G为剪切