
第七章 连续时间信号与系统的复频域分析.doc

ys****39










亲,该文档总共26页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第七章连续时间信号与系统的复频域分析.doc
第七章连续时间信号与系统的复频域分析1、内容简介在连续时间信号与系统的复频域分析中,首先介绍了利用Laplace变换进行连续时间信号的复频域分析和连续时间系统的复频域分析。在此基础上,分析了系统函数及其与系统特性的关系,并介绍了系统的复频域方框图表示。最后介绍了用MATLAB实现连续时间系统的复频域分析。2、学习目标1.熟练掌握单边Laplace变换及其基本性质和Laplace反变换。(双边Laplace变换不要求)2.掌握用单边Laplace求解连续系统响应的零输入响应和零状态响应。3.重点掌握系统的传

第七章 连续时间信号与系统的复频域分析.doc
第七章连续时间信号与系统的复频域分析1、内容简介在连续时间信号与系统的复频域分析中,首先介绍了利用Laplace变换进行连续时间信号的复频域分析和连续时间系统的复频域分析。在此基础上,分析了系统函数及其与系统特性的关系,并介绍了系统的复频域方框图表示。最后介绍了用MATLAB实现连续时间系统的复频域分析。2、学习目标1.熟练掌握单边Laplace变换及其基本性质和Laplace反变换。(双边Laplace变换不要求)2.掌握用单边Laplace求解连续系统响应的零输入响应和零状态响应。3.重点掌握系统的传

连续时间系统的复频域分析.doc
因而拉普拉斯变换分析法常称为复频域分析法。拉普拉斯变换分析法和傅里叶变换分析法都是建立在线性非时变系统的齐次性可迭加性基础上的。只是信号分解的基本单元函数不同。(1)拉普拉斯变换的数学定义和物理意义(2)拉普拉斯变换的性质及计算方法(3)连续时间系统的复频域分析法(4)系统函数的定义§5.3拉普拉斯变换的收敛域由上面的讨论可知,连续时间信号ft的拉普拉斯变换(以下简称拉氏变换)式Fs是否存在,取决于ft乘以衰减因子以后是否绝对可积,即:受迫分量自然分量受迫分量自然分量例5-15图5-18中,已知C11F,
连续时间信号与系统的频域分析.ppt
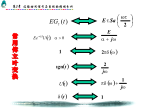
常用傅立叶变换3.5连续时间系统的频域分析一、系统函数(传输函数):1、定义:2、求法:1)从定义求;2)从方程求;3)从冲激响应求;.4)从系统框图求;5)从电路图求.例:求系统函数H(j)。二、系统零状态响应:三、系统频率特性:MATLAB的计算机仿真:四、非周期信号激励下系统的零状态响应解题步骤例:五、系统全响应:六、周期信号通过线性系统2、正弦信号:3、任意周期信号:例:图示系统,若激励如图所示,求响应i(t)。练习:图示系统,频率特性如图所示,求响应y(t)。其中

连续时间LTI系统的复频域分析.docx
实验六:连续时间LTI系统的复频域分析一、实验目的1、掌握拉普拉斯变换的物理意义、基本性质及应用。2、掌握用拉普拉斯变换求解连续时间LTI系统的时域响应。3、掌握系统函数的概念,掌握系统函数的零、极点分布(零、极点图)与系统的稳定性、时域特性等之间的相互关系。4、掌握用MATLAB对系统进行变换域分析的常用函数及编程方法。二、实验原理1、连续时间LTI系统的复频域描述拉普拉斯变换(TheLaplacetransform)主要用于系统分析。描述系统的另一种数学模型就是建立在拉普拉斯变换基础上的“系统函数(S
