
数学模型 运用层次分析法决策考研学校的选择.doc

yy****24




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

数学模型 运用层次分析法决策考研学校的选择.doc
运用层次分析法决策考研学校的选择摘要层次分析法,这是一种定性和定量相结合的、系统化、层次化的分析方法,能有效处理某些实际问题。关键词层次分析法人们在处理一些决策问题时候,要考虑的因素有多有少,有大有小,但是有一个共同的特点是它们通常都涉及经济、社会、人文等方面的因素。在作比较、判断、评价、决策时,这样因素的重要性、影响力或者优先程度往往难以量化,人的主观选择(当然要根据客观实际)会起着相当主要的作用,这就给用一般是数学方法解决问题带来了本质的困难。T.L.Saaty等人在20世纪70年代提出了一种能有效处
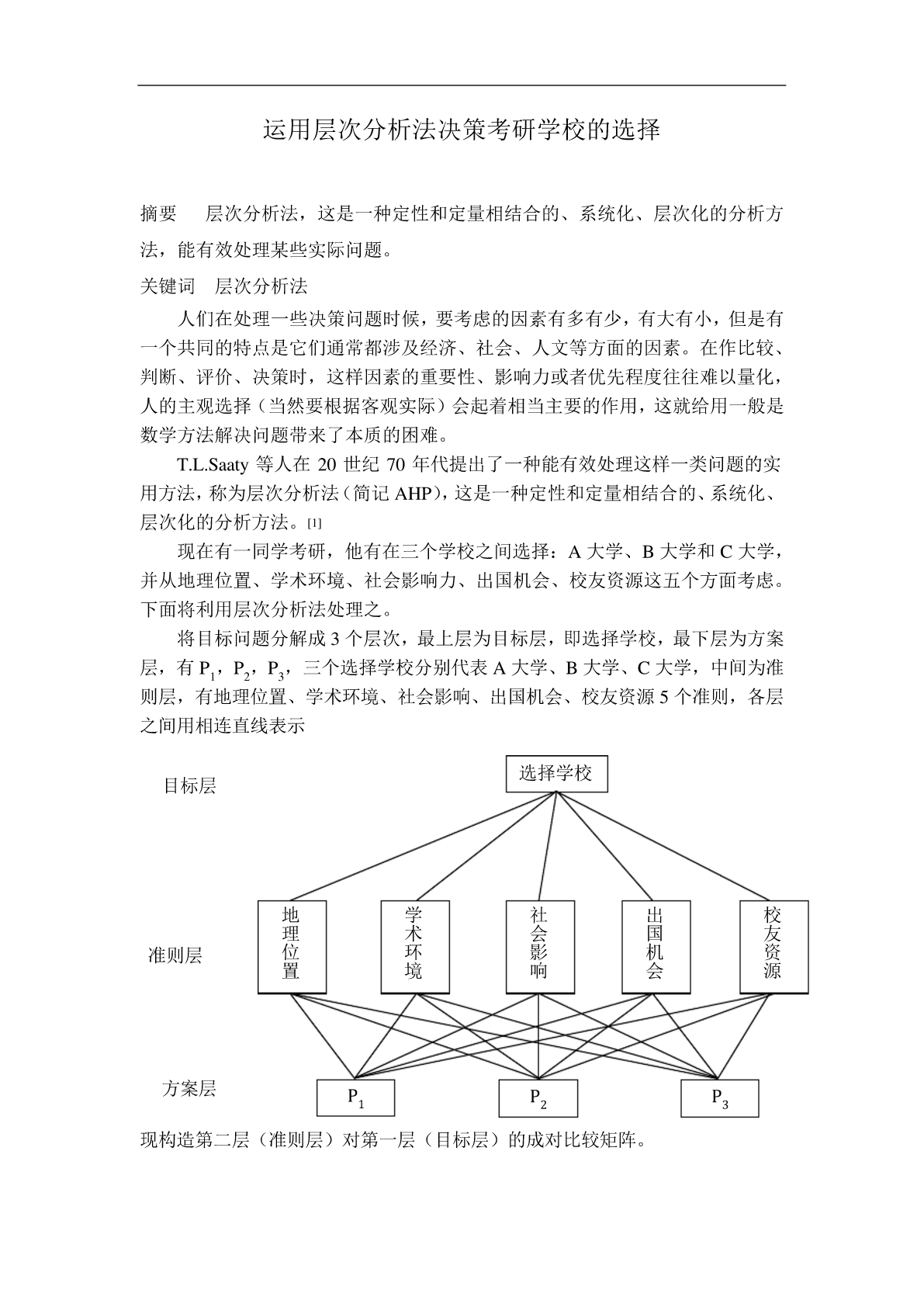
数学模型 运用层次分析法决策考研学校的选择.pdf
运用层次分析法决策考研学校的选择摘要层次分析法,这是一种定性和定量相结合的、系统化、层次化的分析方法,能有效处理某些实际问题。关键词层次分析法人们在处理一些决策问题时候,要考虑的因素有多有少,有大有小,但是有一个共同的特点是它们通常都涉及经济、社会、人文等方面的因素。在作比较、判断、评价、决策时,这样因素的重要性、影响力或者优先程度往往难以量化,人的主观选择(当然要根据客观实际)会起着相当主要的作用,这就给用一般是数学方法解决问题带来了本质的困难。T.L.Saaty等人在20世纪70年代提出了一种能有效处
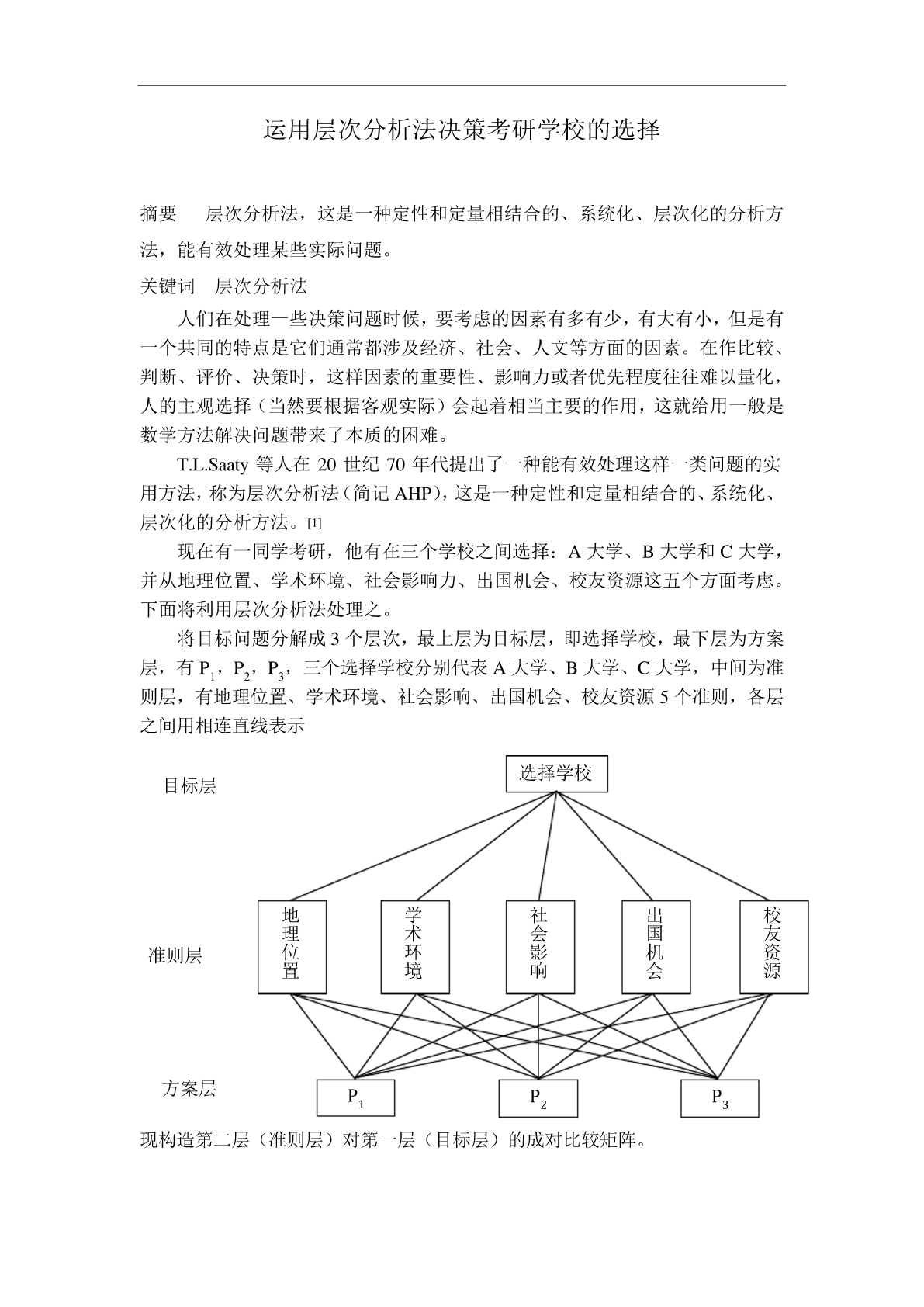
数学模型 运用层次分析法决策考研学校的选择.pdf
运用层次分析法决策考研学校的选择摘要层次分析法,这是一种定性和定量相结合的、系统化、层次化的分析方法,能有效处理某些实际问题。关键词层次分析法人们在处理一些决策问题时候,要考虑的因素有多有少,有大有小,但是有一个共同的特点是它们通常都涉及经济、社会、人文等方面的因素。在作比较、判断、评价、决策时,这样因素的重要性、影响力或者优先程度往往难以量化,人的主观选择(当然要根据客观实际)会起着相当主要的作用,这就给用一般是数学方法解决问题带来了本质的困难。T.L.Saaty等人在20世纪70年代提出了一种能有效处

运用层次分析法决策考研学校的选择.pdf
运用层次分析法决策考研学校的选择学生姓名:QQQ学生学号:xxxxxxxxxxx院系班级:10级数学与应用数学(2)班指导老师:QQQ摘要人们在处理一些决策问题的时候,要考虑的因素有多有少,有大有小,但是有一个共同的特点是它们通常都涉及经济、社会、人文等方面的因素。在作比较、判断、评价、决策时,这样因素的重要性、影响力或者优先程度往往难以量化,人的主观选择会起着相当主要的作用,这类问题处理起来往往比较困难,然而T.L.Saaty等人在20世纪70年代提出了一种能有效处理这样一类问题的实用方法,称为层次分析

运用层次分析法决策考研学校的选择.pdf
运用层次分析法决策考研学校的选择学生姓名:QQQ学生学号:xxxxxxxxxxx院系班级:10级数学与应用数学(2)班指导老师:QQQ摘要人们在处理一些决策问题的时候,要考虑的因素有多有少,有大有小,但是有一个共同的特点是它们通常都涉及经济、社会、人文等方面的因素。在作比较、判断、评价、决策时,这样因素的重要性、影响力或者优先程度往往难以量化,人的主观选择会起着相当主要的作用,这类问题处理起来往往比较困难,然而T.L.Saaty等人在20世纪70年代提出了一种能有效处理这样一类问题的实用方法,称为层次分析
