内容提供者
垂径定理公开课.ppt
2024-09-02
10金币
807KB
22页
qw****27
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共22页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
垂径定理.1.2 垂径定理.ppt
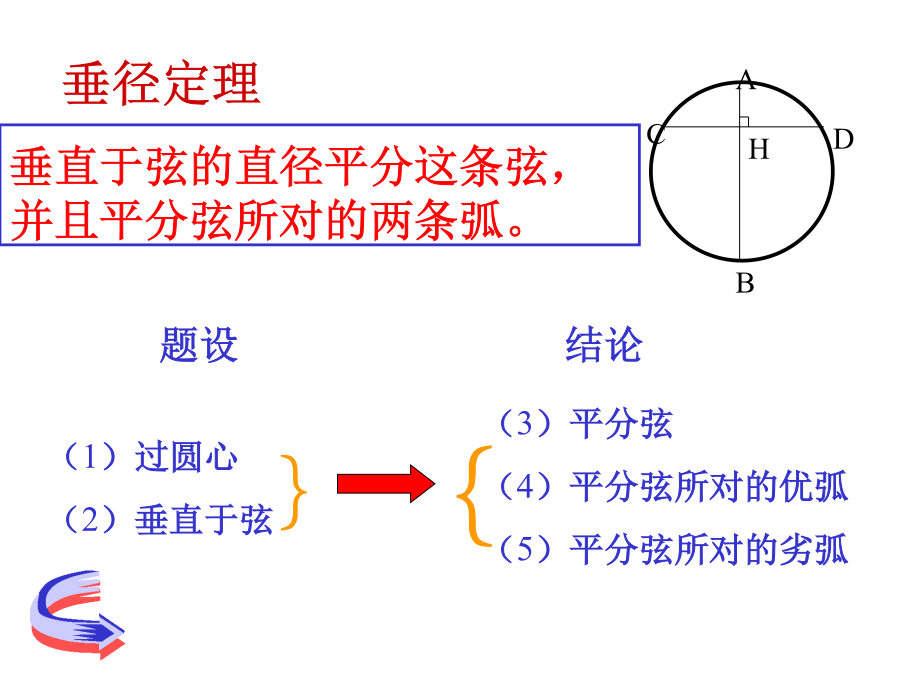
24.1.2OOO证明结论垂径定理①直线CD过圆心O②CD⊥AB如果交换垂径定理的题设和结论的部分语句，会有一些什么样的结论呢？①直线CD过圆心③AM=BM推论1.(1)平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。O推论1:(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;O推论1:(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。小结判断赵州桥又名安济桥，建于隋大业(公元605-618)年间，距今已1400年，是著名匠师李春建造。主桥拱是圆弧形，跨度（弧所对的弦长3
2024-09-26
16
1.9MB
垂径定理公开课.ppt
垂径定理的应用1、已知：如图，⊙O中，弦AB∥CD，AB＜CD，直径MN⊥AB，垂足为E，交弦CD于点F.图中相等的线段有.图中相等的劣弧有.垂径定理1、已知：如图，⊙O中，弦AB∥CD，AB＜CD，直径MN⊥AB，垂足为E，交弦CD于点F.图中相等的线段有AE=BE,CF=DF,MO=NO图中相等的劣弧有.讨论例41300多年前，我国隋朝建造的赵州石拱桥（如图）的桥拱是圆弧形，它的跨度（弧所对是弦的长）为37.4米，拱高（弧的中点到弦的距离，也叫弓形高）为7.2米，求桥拱的半径（精确到0.1米）.解：如
2024-09-02
10
807KB
垂径定理.1.2垂径定理[1].ppt
24.1.2垂径定理·辨析定理的应用条件：解得：R≈27．9（m）1．如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．2．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．巩固训练⌒4、弓形的弦长为6cm，弓形的高为2cm，则这弓形所在的圆的半径为.5、已知P为⊙O内一点，且OP＝2cm，如果⊙O的半径是3cm，那么过P点的最短的弦等于.活动三说一说不经历风雨，怎么见彩虹
2024-09-25
16
1.6MB
垂径定理.1 垂径定理的应用.ppt
24.1垂径定理的应用乌鲁木齐市第七中学3.如图,在⊙O中弦AB⊥AC,OM⊥AB,ON⊥AC,垂足分别为M,N,且OM=2,0N=3,则AB=,AC=,OA=练一练1、辅助线：连半径、作弦心距小结与思考快乐学习与君共勉
2024-09-26
16
1.5MB
垂径定理.1.2垂径定理cyz.ppt
24.1.2垂直于弦的直径１．（１）圆是轴对称图形吗？③AM=BM,如图理由是:下列图形是否具备垂径定理的条件？例１．如图，在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。求证：AC=BDA①直线CD过圆心O②CD⊥AB①直线CD过圆心O③AM=BM(AB不是直径)垂径定理及逆定理例2.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).解：如图，用表示桥拱，所
2024-09-25
16
1.6MB