
统计回归模型.pdf

qw****27







亲,该文档总共44页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

《统计回归模型》.ppt
整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件整理课件

统计回归模型.pptx
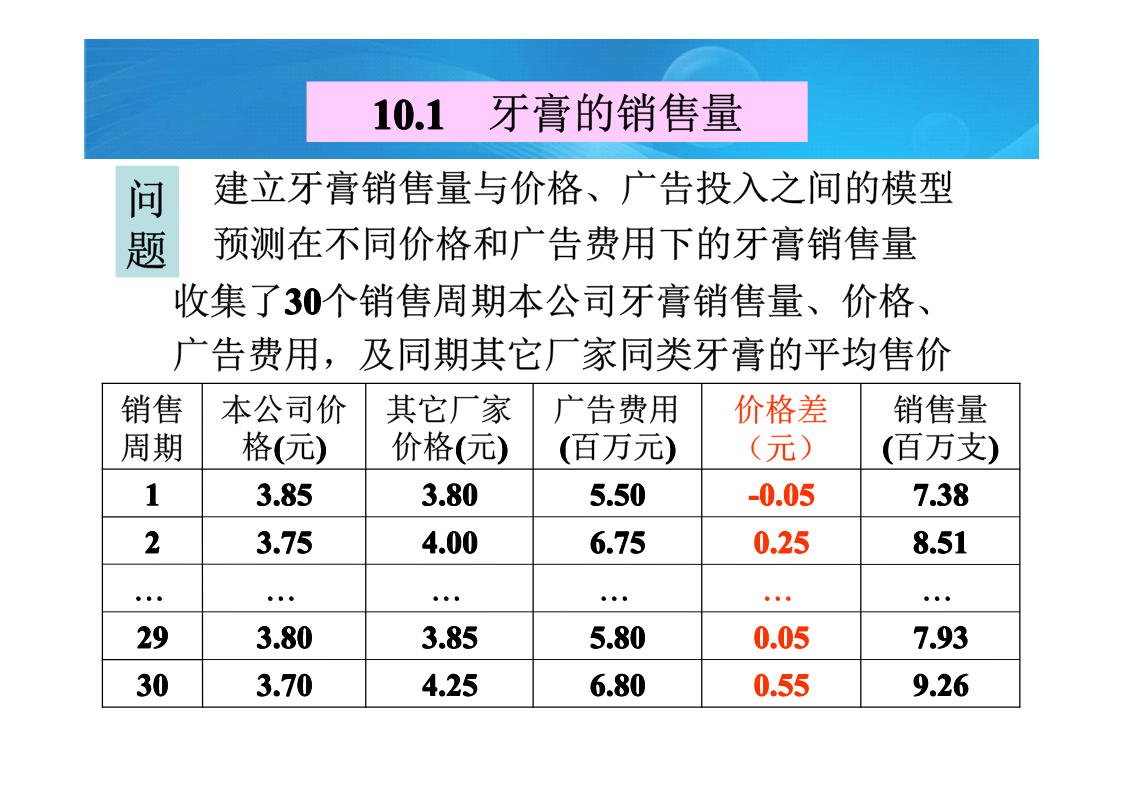
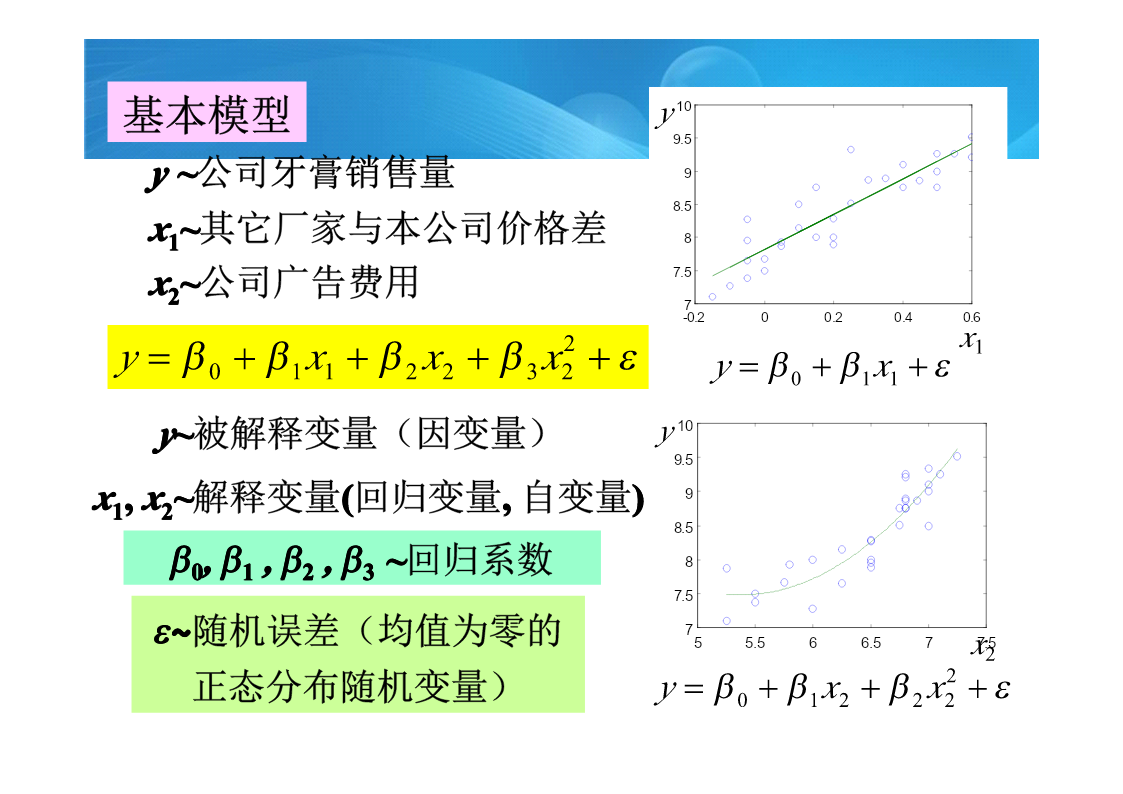
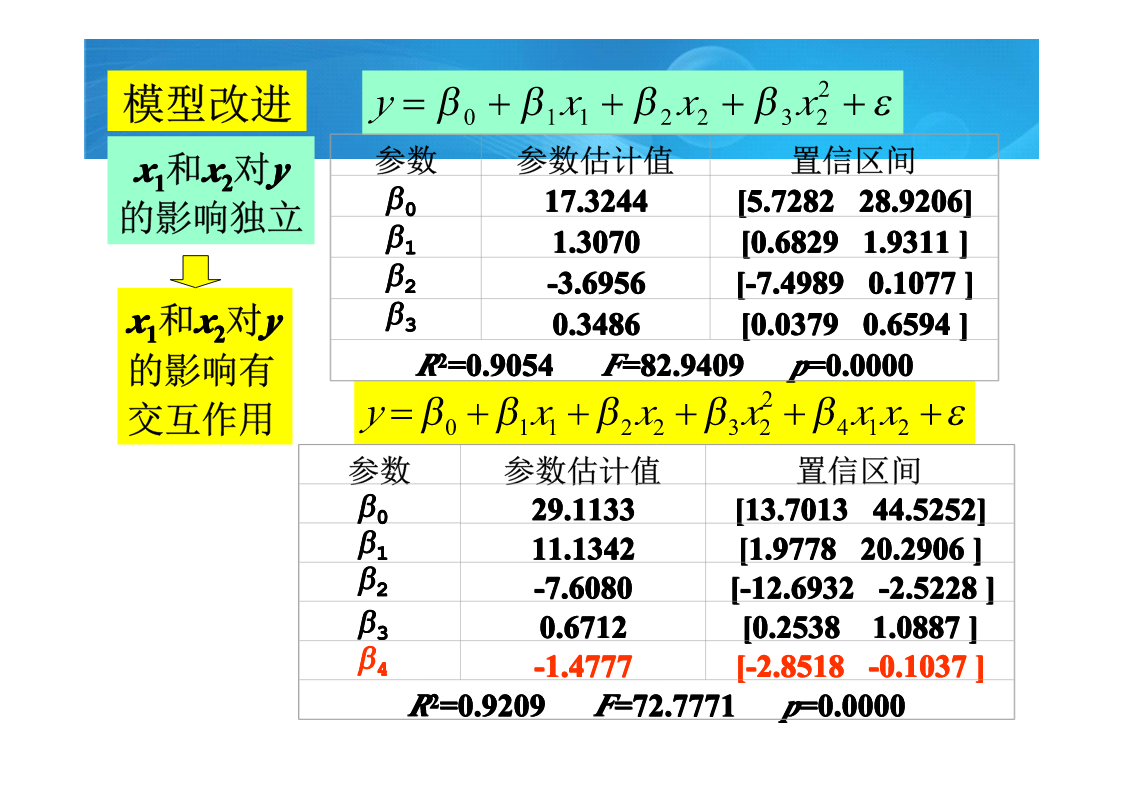
统计回归模型回归模型是用统计分析方法建立的最常用的一类模型1牙膏的销售量基本模型MATLAB统计工具箱结果分析销售量预测模型改进两模型销售量预测比较x2=6.5交互作用影响的讨论完全二次多项式模型2软件开发人员的薪金分析与假设模型求解残差分析方法去掉异常数据后的结果模型应用对定性因素(如管理、教育),可以引入0-1变量处理,0-1变量的个数应比定性因素的水平少13酶促反应线性化模型线性化模型结果分析[beta,R,J]=nlinfit(x,y,’model’,beta0)非线性模型结果分析混合反应模型o~

统计回归模型.ppt
第十章统计回归模型回归模型是用统计分析方法建立的最常用的一类模型10.1牙膏的销售量基本模型MATLAB统计工具箱结果分析销售量预测模型改进两模型销售量预测比较x2=6.5交互作用影响的讨论完全二次多项式模型10.2软件开发人员的薪金分析与假设模型求解残差分析方法进一步的模型去掉异常数据后的结果模型应用对定性因素(如管理、教育),可以引入0-1变量处理,0-1变量的个数应比定性因素的水平少110.3酶促反应基本模型线性化模型线性化模型结果分析[beta,R,J]=nlinfit(x,y,’model’,b

统计回归模型.pdf
统计回归模型10.1牙膏的销售量10.2软件开发人员的薪金10.3酶促反应10.4投资额与国民生产总值和物价指数55128.5d6d.net福彩3D数学建模的基本方法机理分析测试分析由于客观事物内部规律的复杂及人们认识程度的限制,无法分析实际对象内在的因果关系,建立合乎机理规律的数学模型。通过对数据的统计分析,找出与数据拟合最好的模型回归模型是用统计分析方法建立的最常用的一类模型•不涉及回归分析的数学原理和方法•通过实例讨论如何选择不同类型的模型•对软件得到的结果进行分析,对模型进行改进10.1牙膏的销售

回归模型与统计.ppt
回归模型与统计软件表1各机组出力方案(单位:兆瓦,记作MW)16表8.2各线路的潮流值(各方案与表1相对应,单位:MW)16对函数拟合,我们可以采用线性,也可以采用非线性的函数.非线性有多项式,三角函数,指数函数等,面对如本问题所示的具体数据,我们当然准备好把这些函数都拿去尝试的打算.不过那是万不得已,没招的情况下才采用的最后招数.我们做实际问题,首先想到的还是采用最简单的方法下手,如果简单的方法都可以完成得很好,当然没必要采用复杂的方法.况且对该赛题,后面还有四个更难的问题在等着我们.我们不能把第一个问
