
隐马尔可夫模型_刘秉权.pdf

qw****27









亲,该文档总共37页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

隐马尔可夫模型_刘秉权.pdf
隐马尔可夫模型刘秉权哈工大智能技术与自然语言处理研究室2006年11月主要内容马尔可夫模型隐马尔可夫模型隐马尔可夫模型的三个基本问题隐马尔可夫模型的基本算法隐马尔可夫模型的应用隐马尔可夫模型2马尔可夫链一个系统有个状态,随着时间推移,系统从NS1,S2,L,SN某一状态转移到另一状态,设qt为时间t的状态,系统在时间t处于状态的概率取决于其在时间的状态,该概率为:Sj1,2,L,t-1P(qt=Sj|qt-1=Si,qt-2=Sk,L)如果系统在t时间的状态只与其在时间t−1的状态相关,则该系统

隐马尔可夫模型.ppt
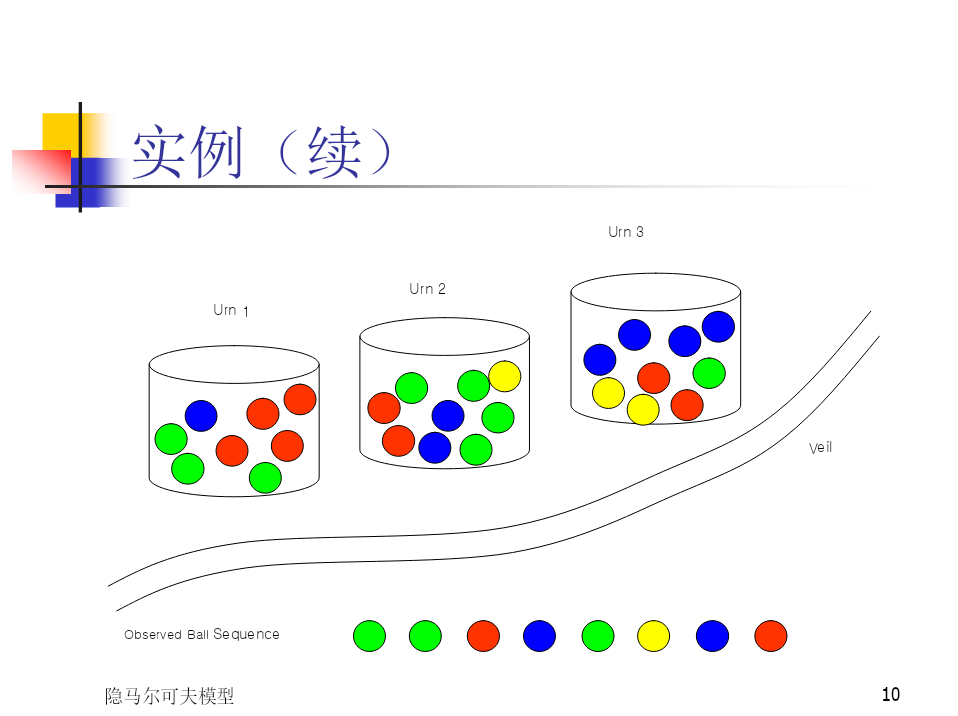
隐马尔可夫模型HiddenMarkovModelHiddenMarkovModel思考题:主要内容一、隐马尔可夫模型的基本概念(1)HMM的基本概念1每个硬币代表一个状态;每个状态有两个观测值:正面H和反面T;每个状态产生H的概率:P(H);每个状态产生T的概率为:1-P(H)对比两个模型可见:马尔可夫模型的观测序列本身就是状态序列;隐马尔可夫模型的观测序列不是状态序列;设有N个篮子,每个都装了许多彩色小球,小球颜色有M种.现在按下列步骤产生出一个输出符号(颜色)序列:按某个初始概率分布,随机的选定一个篮

隐马尔可夫模型简介.ppt
隐马尔可夫模型简介假设定义问题算法算法:向前算法(一)算法:向前算法(二)变化例子:病情转化例子:词性标注应用资源总结

隐马尔可夫模型的原理与实现.pdf
国外医学生物医学工程分册2002年第25卷第6期·352·隐马尔可夫模型的原理与实现刘河生,高小榕,杨福生(清华大学电机工程与应用电子技术系,北京100084)摘要:隐马尔可夫模型正在被愈来愈多地引入到生物医学信号的处理中。本文旨在简述它的基本原理和实现中的问题,并且用简洁的列表形式总结它的算法步骤。关键词:隐马尔可夫模型;信号处理;实现算法中图分类号:R311;R318文献标识码:A文章编号:100121110(2002)0620253207TheoryofhiddenMarkovmodelingand

连续型隐马尔可夫模型.pdf
第32卷第1期华中师范大学学报(自然科学版)Vol.32No.11998年3月JOURNALOFCENTRALCHINANORMALUNIVERSITY(Nat.Sci.)Mar.1998连续型隐马尔可夫模型(HMM)参数与语音识别3李四信韦岗(华南理工大学电子与通信工程系,广州510641)摘要提出了一种新的连续型隐马尔可夫模型(HMM)的概率密度函数,并导出了一系列的参数寻优迭代公式,与常用的概率密度函数相比,它的运算量较小,且不易产生计算时的上溢与下溢问题,把它用于HMM语音识别,效果较好.关键词连
