03-多元线性回归模型.pdf

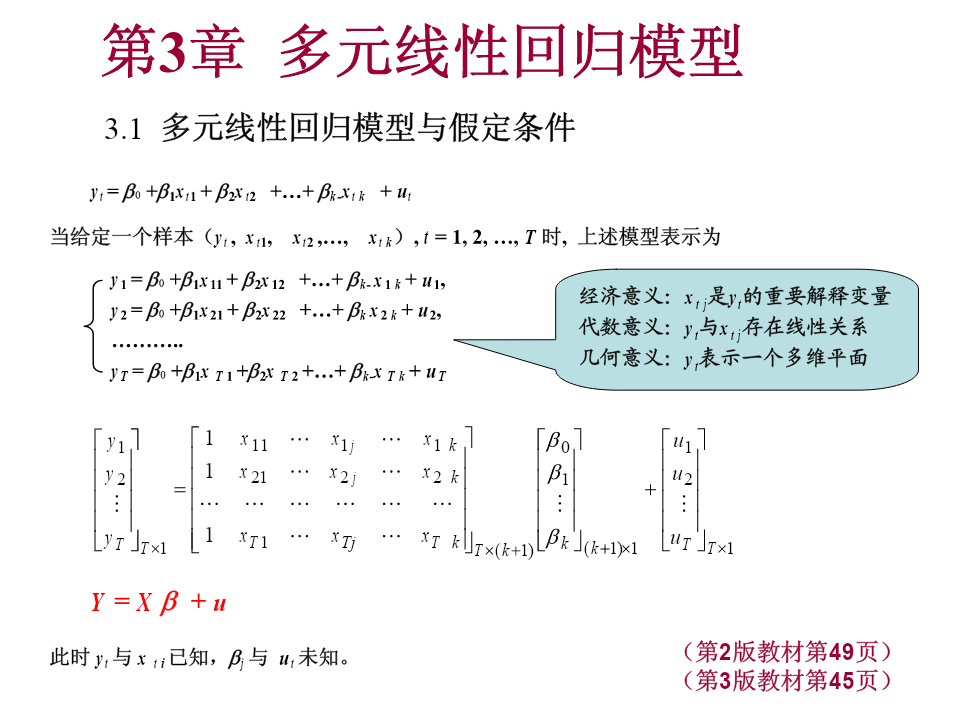
第3章多元线性回归模型

多元线性回归模型与假定条件
最小二乘法（OLS）
最小二乘估计量的特性
可决系数
显著性检验与置信区间
预测
预测的评价指标
建模过程中应注意的问题
案例分析
第3章多元线性回归模型

3.1多元线性回归模型与假定条件

yt=β0+β1xt1+β2xt2+…+βk-xtk+ut

当给定一个样本（yt,xt1,xt2,…,xtk）,t=1,2,…,T时,上述模型表示为

y1=β0+β1x11+β2x12+…+βk-x1k+u1,
经济意义：xtj是yt的重要解释变量
y2=β0+β1x21+β2x22+…+βkx2k+u2,
代数意义：y与x存在线性关系
………..ttj
几何意义：yt表示一个多维平面
yT=β0+β1xT1+β2xT2+…+βk-xTk+uT

⎡y1⎤⎡1x11"x1j"1xk⎤⎡β0⎤⎡u1⎤
⎢⎥⎢⎥⎢⎥⎢⎥
y1x21"x2j"2xkβu
⎢2⎥=⎢⎥⎢1⎥+⎢2⎥
""""""⎢#⎥⎢⎥⎢#⎥⎢#⎥
⎢⎥⎢⎥⎢⎥⎢⎥
y1x"x"xβu
⎣T⎦T×1⎣⎢T1TjTk⎦⎥T×(k1+⎣)(k⎦k+1)×1⎣T⎦T×1

Y=Xβ+u

此时yt与xti已知，βj与ut未知。（第2版教材）
（第3版教材）
3.1多元线性回归模型与假定条件

为保证得到最优估计量，回归模型应满足如下假定条件：
⎡0⎤
假定（）：⎢⎥
1E(u)=0=⎢#⎥
⎣⎢0⎦⎥
假定（2）：误差项同方差、非自相关
1⎡0⎤0
⎢⎥
220%0
Var(u)=E(uˆuˆ')=σI=σ⎢⎥
0⎣⎢0⎦⎥1

假定（3）：解释变量与误差项相互独立。E(X'u)=0

假定（4）：解释变量之间线性无关。rk(X'X)=rk(X)=k+1

假定（5）：解释变量是非随机的，且当T→∞时，T–1X'X→Q

其中Q是一个有限值的非退化矩阵。（第2版教材）
（第3版教材）
3.2最小二乘法（OLS）

最小二乘(OLS)法的原理是求残差平方和最小。代数上是求极值问题。

minS=(Y-Xβˆ)'(Y-Xβˆ)=Y'Y-βˆ'X'Y-Y'Xβˆ+βˆ'X'Xβˆ

=Y'Y-2βˆ'X'Y+βˆ'X'Xβˆ

因为Y'Xβˆ是一个标量，所以有Y'Xβˆ=βˆ'X'Y。上式的一阶条件为：

∂S
=-2X'Y+2X'Xβˆ=0
∂βˆ

X'Y=X'Xβˆ

因为(X'X)是一个非退化矩阵（假定（5）），所以有

ˆ-1
β=(X'X)X'Y
（第2版教材）
（第3版教材）
3.2最小二乘法（OLS）

βˆ的最小二乘(OLS)估计公式也可以用下面的方式推导。

对估计的回归模型Y=Xβˆ+uˆ左乘一个X'，

X'Y=X'Xβˆ+X'uˆ

根据（最小二乘）估计的回归函数的性质（4），X'uˆ=0有

X'Y=X'Xβˆ

ˆ-1
β=(X'X)X'Y
高斯—马尔可夫定理：若前述假定条件成立，OLS估计量是
最佳线性无偏估计量。βˆ具有无偏性，最小方差特性，一致性。

求出βˆ，估计的回归模型写为

Y=Xβˆ+uˆ=Yˆ+uˆ
例题3.1

obsYX1X2
158956
248853
363760
468670
573778
698584
798491
878682
91083100
10885120

Y：某商品需求量
Yˆ=113.83-8.36X1+0.18X2X1：该商品价格
X2：消费者平均收入
(4.0)(-3.6)(0.9)
（第2版教材）
2
R=0.88,F=26.4,T=10（第3版教材）
3.3最小二乘（OLS）估计量的特性

1．βˆ的分布
（第2版教材）
（第3版教材）
E(βˆ)=E[(X'X)-1X'Y]=E[(X'X)-1X'(Xβ+u)]

=β+(X'X)-1X'E(u)=β

Var(βˆ)=E[(βˆ–β)(βˆ–β)']=E[(X'X)-1X'uu'X(X'X)-1]

=E[(X'X)-1X'σ2IX(X'X)-1]=σ2(X'X)-1

因为u∼N(0,σ2I)，Y∼N(Xβ,σ2I)，βˆ=(X'X)-1X'Y，

βˆ是Y的线性函数，所以

ˆ2-1
β∼N(β,σ(X'X))。
3.3最小二乘（OLS）估计量的特性

2.残差的方差

s2=σˆ2=uˆ'uˆ/(T–k-1)

s2是σ2的无偏估计量，E(s2)=E(σˆ2)=σ2。

βˆ的估计的方差协方差矩阵是

∧
Var(βˆ)=s2(X'X)-1=σˆ2(X'X)-1

（第2版教材）
（第3版教材）
3.4可决系数（R2）

1.决系数）多重确定系数（多重可

Y=Xβˆ+uˆ=Yˆ+uˆ，STS=SRS+ESS

SSRY'Yˆˆ−Ty2
R2==
SSTYY-′Ty