
主成分分析,多元回归分析.ppt

as****16




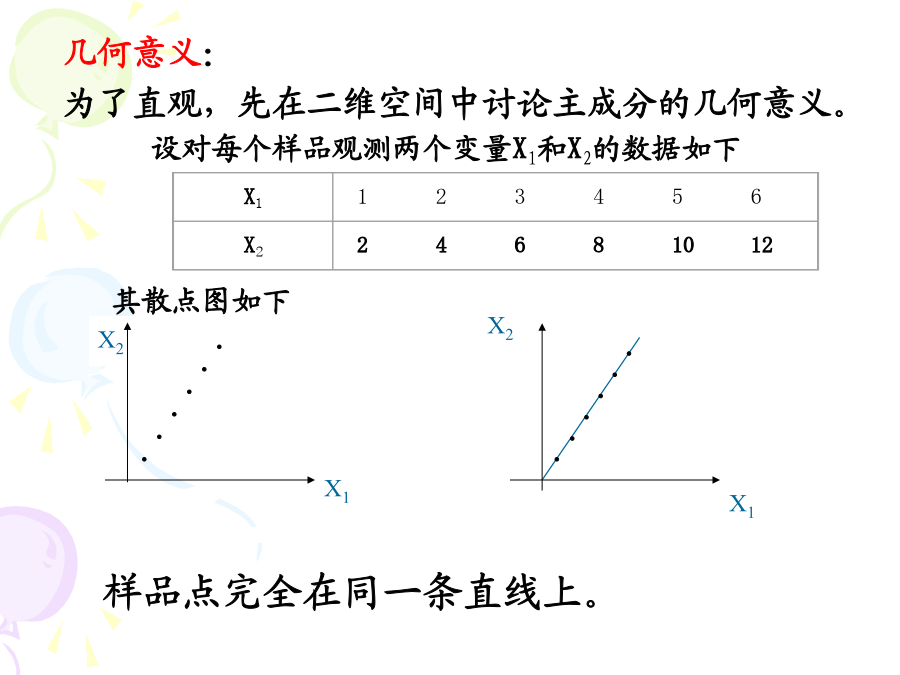
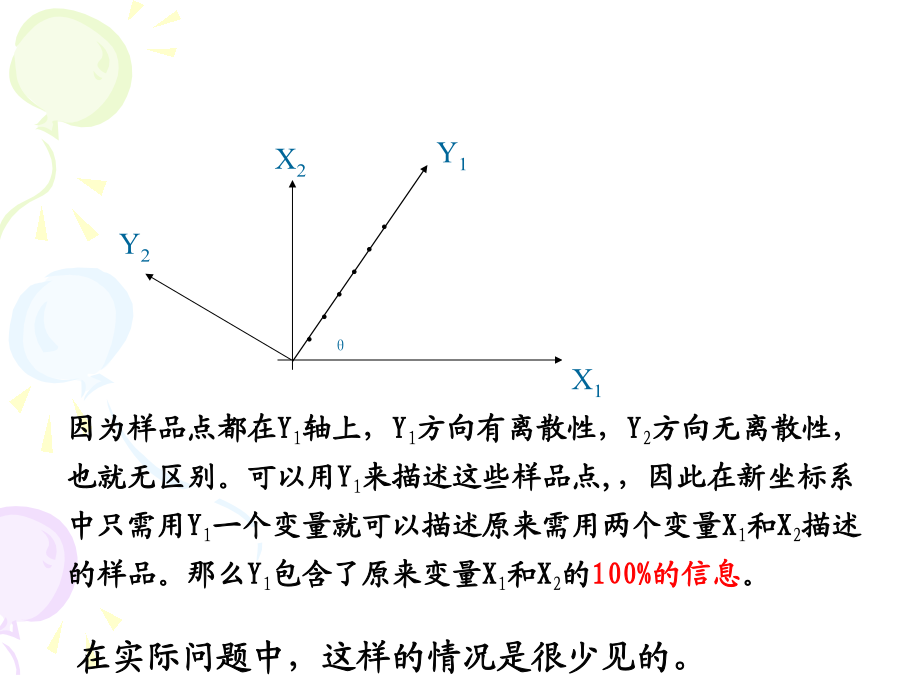
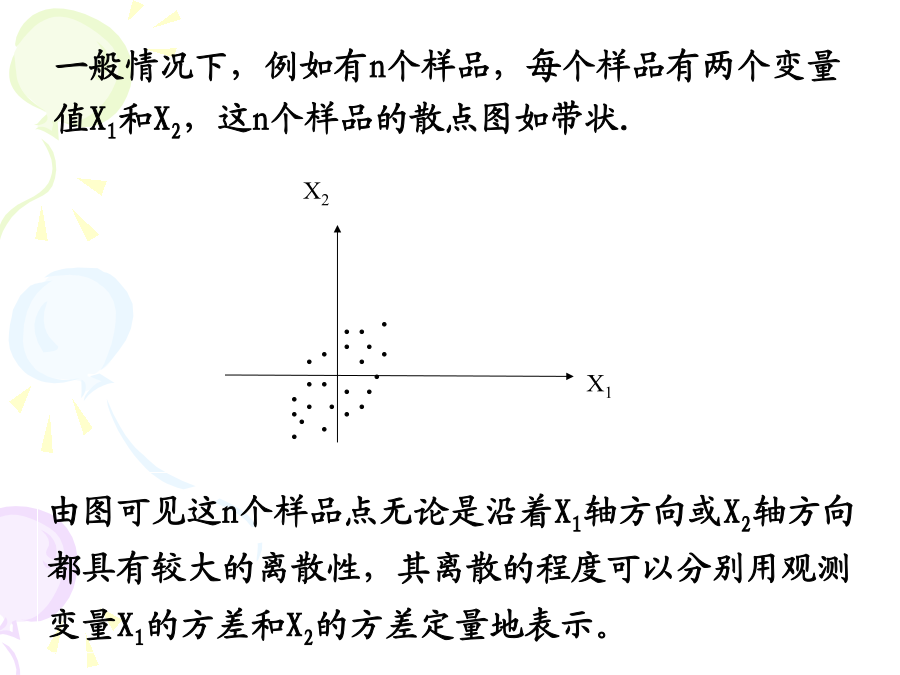
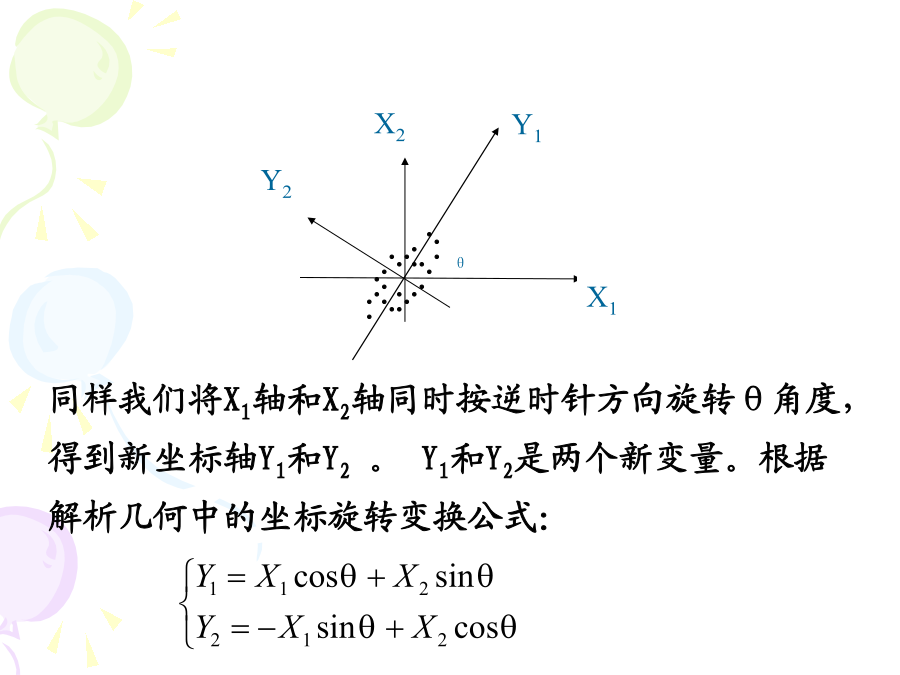


亲,该文档总共37页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

主成分分析,多元回归分析.ppt
第五章主成分分析什么是主成分分析在综合评价工业企业的经济效益中,考核指标有:1每百元固定资产原值实现产值、2每百元固定资产原值实现利税、3每百元资金实现利税、4每百元工业总产值实现利税、5每百元销售收入实现利税、6每吨标准煤实现工业产值、7每千瓦电力实现工业产值、8全员劳动生产率、9每百元流动资金实现的产值指标间信息有重叠,指标数量又多。经过主成分分析计算,最后确定选择了2个主成分作为综合评价工业企业经济效益的依据,变量数由9个减少到2个,这两个主成分代表的信息达91.6%,使所研究的问题简化。第一节主成

山仔水库蓝藻水华因子主成分多元回归分析.docx
山仔水库蓝藻水华因子主成分多元回归分析山仔水库蓝藻水华因子主成分多元回归分析概述:水库是一种重要的淡水资源储存和供应方式。然而,水体中蓝藻水华的出现可能会威胁到水库的水质和生态环境。因此,研究和分析影响蓝藻水华的因子对于保护和管理水库具有重要意义。本文将以山仔水库为例,应用主成分分析和多元回归分析方法,探究影响蓝藻水华的主要因素。一、山仔水库概况山仔水库位于XX省XX市,它是该地区重要的水源之一。山仔水库的主要功能是供应生活用水和灌溉用水。然而,最近几年,山仔水库频繁出现蓝藻水华,严重影响了水库的水质和生

基于主成分分析的多元回归算法在电力预测中的应用.docx
基于主成分分析的多元回归算法在电力预测中的应用基于主成分分析(PCA)的多元回归算法在电力预测中的应用摘要:电力预测在能源行业中起着重要作用,能够为能源供应和需求的平衡提供支持。然而,由于电力系统复杂性和不确定性的特点,电力预测存在一定的困难。为了提高电力预测的准确性和可靠性,研究者开始采用多元回归算法,并将主成分分析(PCA)应用于该算法中。本文重点介绍了主成分分析的原理和步骤,并详细说明了利用主成分分析的多元回归算法在电力预测中的应用。实证结果表明,基于主成分分析的多元回归算法在电力预测中具有较好的效

主成分分析方法在主成分分析方法中的应用.docx
主成分分析与因子分析及SPSS实现(一):原理与方法(2014-09-0813:33:57)转载▼一、主成分分析(1)问题提出在问题研究中,为了不遗漏和准确起见,往往会面面俱到,取得大量的指标来进行分析。比如为了研究某种疾病的影响因素,我们可能会收集患者的人口学资料、病史、体征、化验检查等等数十项指标。如果将这些指标直接纳入多元统计分析,不仅会使模型变得复杂不稳定,而且还有可能因为变量之间的多重共线性引起较大的误差。有没有一种办法能对信息进行浓缩,减少变量的个数,同时消除多重共线性?这时,主成分分析隆重登

主成分分析分析报告.pptx
主成分分析分析报告引言主成分分析简介数据准备与预处理主成分提取与分析结果解释与讨论结论与展望引言目的本报告主要介绍主成分分析的基本原理、实施步骤、结果解释以及应用场景。主成分分析简介数据准备与预处理对获取的数据进行清洗,去除重复、错误或不完整的数据,确保数据的准确性和完整性。数据标准化主成分提取与分析结果解释与讨论结论与展望在进行主成分分析时,可能存在主观因素影响结果的解释性,未来可以尝试采用不同的方法进行主成分提取和解释。THANKS
