双因素实验回归分析和方差分析的转化.pdf

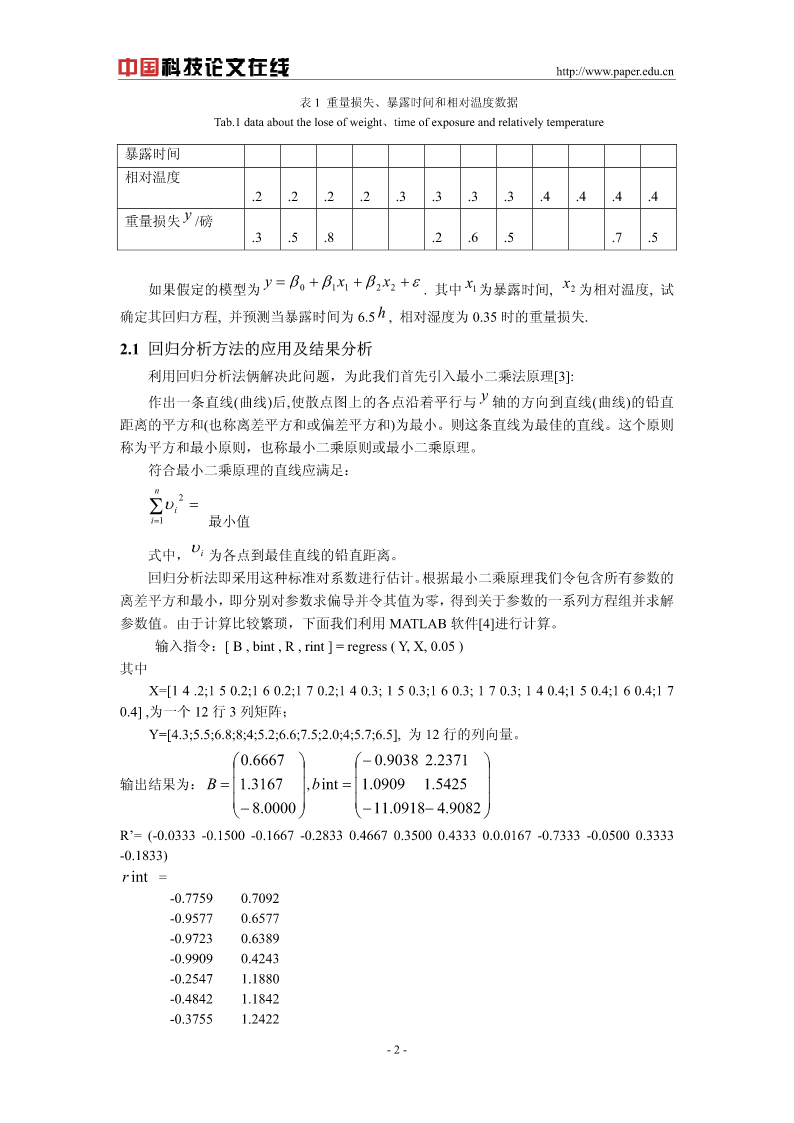
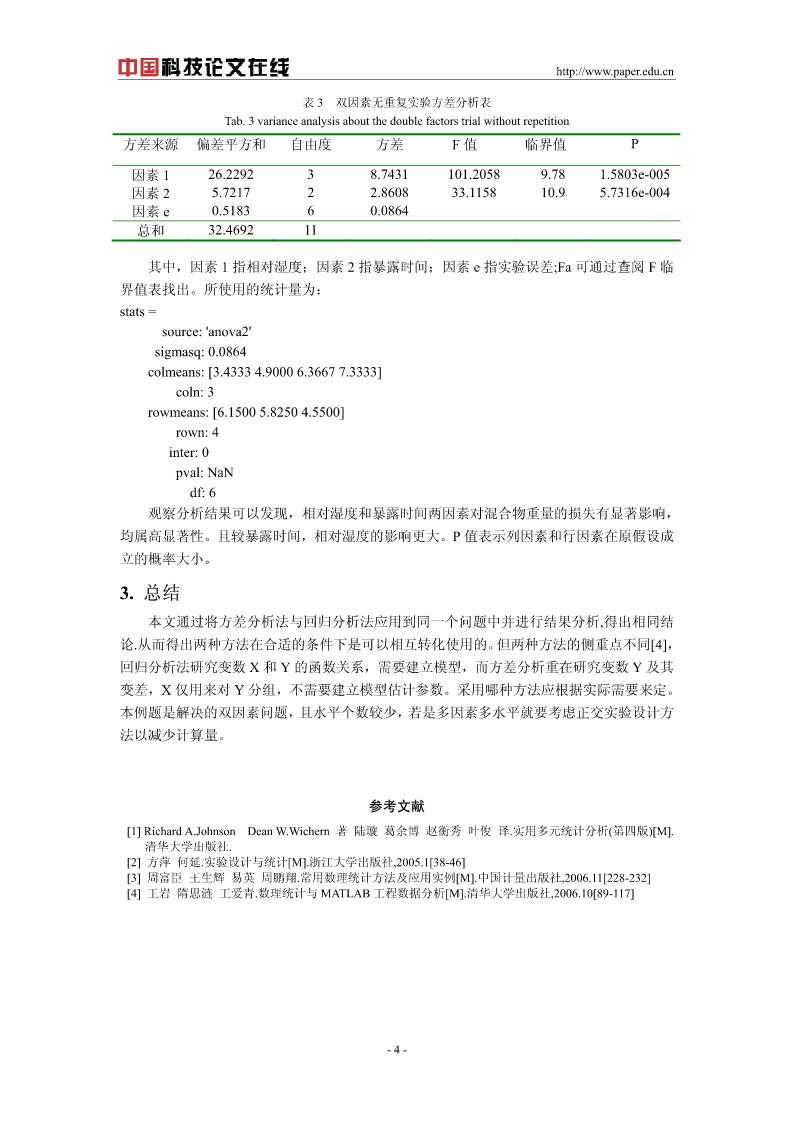
http://www.paper.edu.cn

双因素实验回归分析和方差分析的转化

李晓燕
新疆大学数学与系统科学学院，乌鲁木齐（830046）
E-mail:[e-mail]
摘要：本文简要介绍了回归分析和方差分析的基本原理，并根据实际问题中的双因素无重
复实验的具体实施情况分别采用回归分析法和方差分析法进行分析讨论。对前者，首先对实
验数据进行认真观测，研究自变量及结果变量的相关性和变化规律，给出假定的回归模型并
对参数及其置信区间进行估计推断；对后者，双因素实验观测数据虽较多，但因素水平较少
的情况下，就可以通过重新调整数据结构设置，使其变为正交实验设计模式，从而可单独对
某因素进行显著性影响的评判，即方差分析。从而得出同一问题在适当条件下两种方法的可
实现性。
关键词：回归分析，方差分析，最小二乘原理，离差平方和，双因素
中图分类号：O212.6

1.引言
在科学实践的许多问题中，常会遇到许多相互联系相互制约的变量，常见的变量之间的
关系大致分为两类：确定性关系和非确定性关系。确定性关系即函数关系，此关系大家较为
熟悉；非确定性关系即相关关系。相关关系是指两个相互关联的变量之间存在着一定的数量
关系，而这种关系并不是完全确定的，当一个变量发生变化时，另一个变量也在一定范围内
有规律的变化。变量间存在相关关系的例子也很多。例如，身高和体重的关系，总体来说，
身高者体也重；在气候、种子、管理等条件基本相同时，施肥量和浇水量多些，亩产量则高
些，但也不会无限制上涨，而是在某个范围内大体上满足这种关系。回归分析就是研究某随
机变量（因变量）与其它一个或多个普通变量（自变量）之间的数量关系，并建立其数学关
系，称为回归方程。如果所建立的方程是线性的，称作线性回归[1]，否则称作非线性回归。
回归分析是解决这种非确定关系的有力工具。
方差分析也是数理统计的基本方法之一，是工农业生产和科学研究中分析数据的一种常
用方法。例如，在化工生产中，原料成分、原料剂量、催化剂和反应时间等因素都会对产品
的质量和数量产生影响，但影响大小各有不同，要想找出对产品的质量和数量产生显著影响
的因素就需要进行实验。而方差分析是通过对观测实验数据的数学处理，来判断一个或多个
因素在水平发生变化时是否会对实验结果产生显著影响，从而选出最优生产条件的一种数理
统计方法。本文所讨论的双因素无重复正交试验设计较简单（读者可参阅文献[2]）。回归分
析法和方差分析法都是工农业生产和科学研究中观测实验数据的常用工具，且在一定条件下
也可以转化使用。本文仅对双因素无重复实验条件下的线性回归分析和方差分析进行讨论。
2.回归分析法和方差分析法的实例应用

我们给出这样一个例子：

例某化学家想要确定一特定的混合物暴露在空气中，其重量的减少y暴露时间x1,暴

露过程中环境的温度x2之间的函数关系。下面给出了12组样本的重量减少与暴露时间、相
对湿度的数据（见下表）：

-1-
http://www.paper.edu.cn

表1重量损失、暴露时间和相对温度数据
Tab.1dataabouttheloseofweight、timeofexposureandrelativelytemperature

暴露时间
相对温度
.2.2.2.2.3.3.3.3.4.4.4.4
重量损失y/磅4424
.3.5.8.2.6.5.7.5

y=β+βx+βx+ε
如果假定的模型为01122.其中x1为暴露时间,x2为相对温度,试
确定其回归方程,并预测当暴露时间为6.5h,相对湿度为0.35时的重量损失.

2.1回归分析方法的应用及结果分析
利用回归分析法俩解决此问题，为此我们首先引入最小二乘法原理[3]:
作出一条直线(曲线)后,使散点图上的各点沿着平行与y轴的方向到直线(曲线)的铅直
距离的平方和(也称离差平方和或偏差平方和)为最小。则这条直线为最佳的直线。这个原则

称为平方和最小原则，也称最小二乘原则或最小二乘原理。

符合最小二乘原理的直线应满足：
n
υ2=
Σi
i=1最小值
υ
式中，i为各点到最佳直线的铅直距离。
回归分析法即采用这种标准对系数进行估计。根据最小二乘原理我们令包含所有参数的
离差平方和最小，即分别对参数求偏导并令其值为零，得到关于参数的一系列方程组并求解
参数值。由于计算比较繁琐，下面我们利用MATLAB软件[4]进行计算。
输入指令：[B,bint,R,rint]=regress(Y,X,0.05)
其中
X=[14.2;150.2;160.2;170.2;140.3;150.3;160.3;170.3;140.4;150.4;160.4;17
0.4],为一个12行3列矩阵；
Y=[4.3;5.5;6.