10 简单线性回归分析.pdf

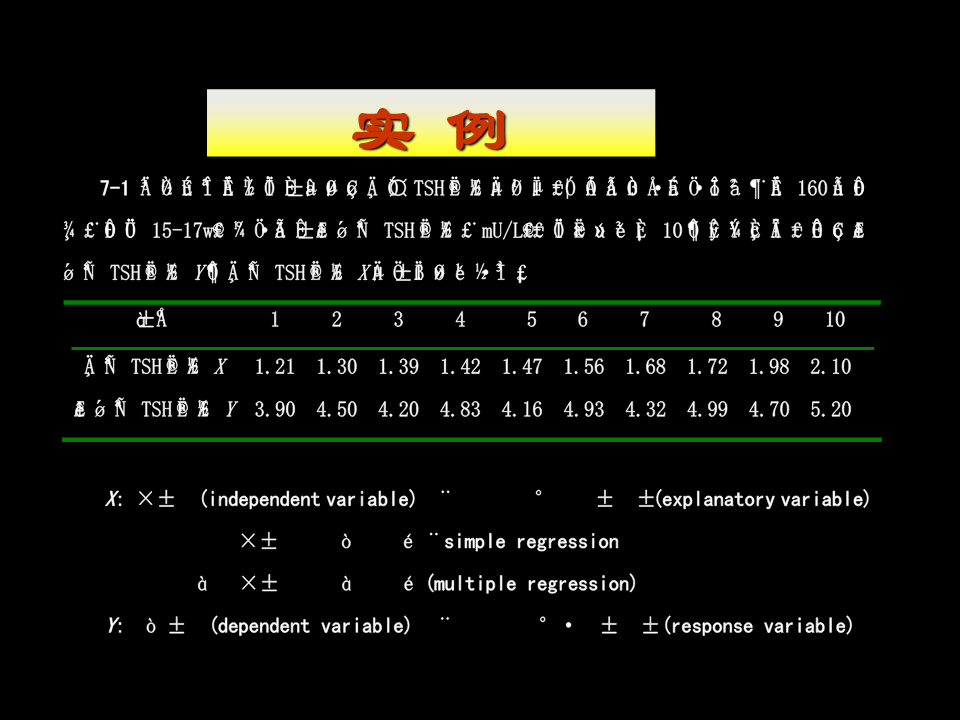
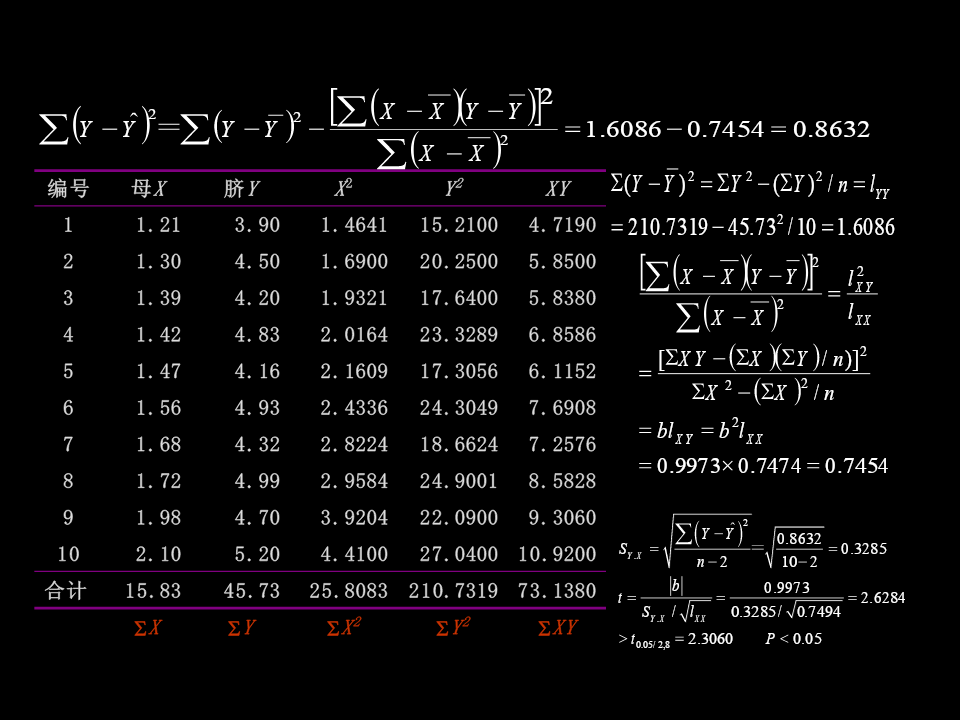
10简单线性回归分析

变量间关系问题：年龄~身高、肺活量~体重、药物剂量与
动物死亡率等。
两个关系：

y(1)依存关系：应变量(dependentvariable)Y随自变量(independent
variable)X变化而变化。——回归分析
(2)互依关系：应变量Y与自变量X间的彼此关系——相关分析
实例
ÀÀ7-1ijҼÉúΪÁË̼ÌÖȱµâµØÇøÄ·Ó¤TSHˮƼµÄ¸Øϵ£¬Ó¦ÓÃÃâÒß²ÅÉä²ÖÎö²â¶¨ÁË160ÃûÔÐ
·½£¨ÔÐÖÜ15-17w£©»°²ÖÃäʱÆê´øѪTSHˮƼ£¨mU/L£©£¬ÏÖËæºú³éÈ¡10¶ÔÊý½ÝÈçÏ£¬ÊÔÇóÆê
´øѪTSHˮƼY¶ÔķѪTSHˮƼXµÄÖ±Ïߺظ鲼³Ì¡£

±´¹Å12345678910

ķѪTSHˮƼX1.211.301.391.421.471.561.681.721.982.10
Æê´øѪTSHˮƼY3.904.504.204.834.164.934.324.994.705.20

X:³À±ÀÀÀ(independentvariable)ÀÀÀ¨ÀÀÀÀÀÀÀÀÀ°ÀÀÀÀ±ÀÀÀÀ±(explanatoryvariable)
ÀÀÀÀÀÀÀÀ³À±ÀÀÀÀÀÀÀÀòÀÀÀÀÀéÀ¨simpleregressionÀÀÀÀ
À´ÀÀ³À±ÀÀÀÀÀÀÀÀ´ÀÀÀÀÀé(multipleregression)
Y:Àò±ÀÀÀ(dependentvariable)ÀÀÀ¨ÀÀÀÀÀÀÀÀÀ°²ÀÀÀ±ÀÀÀÀ±(responsevariable)
散点图

5.5

5.0

4.5
（mU/L）Y

4.0
新生儿脐带血TSH水平

3.5
1.01.21.41.61.82.02.2
母血TSH水平（mU/L）X
图7-1母血与新生儿脐带血TSH水平散点图X
函数关系：确定。例如园周长与半径：y=2πr。
回归关系：不确定。例如血压和年龄的关系，称为直线回
归(linearregression)。

目的：
建立直线回归方程(linearregressionequation)
一、直线回归方程
一般表达式：
YˆabX
a：截距(intercept)，直线与Y轴交点的纵坐标。
b：斜率(slope)，回归系数(regressioncoefficient)。
意义：X每改变一个单位，Y平均改变b个单位。
b>0，Y随X的增大而增大（减少而减少）——斜上；
b<0，Y随X的增大而减小（减少而增加）——斜下；
b=0，Y与X无直线关系——水平。
｜b｜越大，表示Y随X变化越快，直线越陡峭。
例71资料的回归方程：Yˆ2.99430.9973X
二、回归方程参数的计算

最小二乘法原则(leastsquaremethod)：使各散点到直
2
线的纵向距离的平方和最小。即使YYˆ最小。
nn
ˆ2ˆ22
Q(YY)(YiYi)YiabXi
i1i1
(XX)(YY)XYXY/nl
bXY
222
(XX)XX/nlXX
aYbX因为直线一定经过“均数”
点
散点图
5.5X

5.0

4.5
YY

4.0

（mU/L）3.5

新生儿脐带血TSH水平3.0

2.5
0.00.20.40.60.81.01.21.41.61.82.02.2
母血TSH水平（mU/L）X
图7-1母血与新生儿脐带血TSH水平散点图X
回归参数计算的实例

编号母X脐YX2Y2XY
lXYXY/n
bXY
11.213.901.464115.21004.719022
lXXXX/n
21.304.501.690020.25005.850073.13815.8345.73/10

31.394.201.932117.64005.838025.808315.832/10
41.424.832.016423.32896.85860.7474
0.9973
51.474.162.160917.30566.11520.7494
61.564.932.433624.30497.6908
XX/n15.83/101.583
71.684.322.822418.66247.2576
81.724.992.958424.90018.5828YY/n45.73/104.573
91.984.703.920422.09009.3060aYbX
102.105.204.410027.040010.92004.5730.