MATLAB 回归分析.ppt

数学建模与matlab软件一、基本统计量二、分布函数的近似求法3、t分布t(n)
概率密度：tpdf(x,n);概率函数：tcdf(x,n)
4、F分布F(n1,n2)
概率密度：fpdf(x,n1,n2);概率函数：fcdf(x,n1,n2)
5、随机数生成：rnd
例生成标准正态分布数据：normrnd(m)
生成(0,1)上均匀分布数据：unitrnd(m)

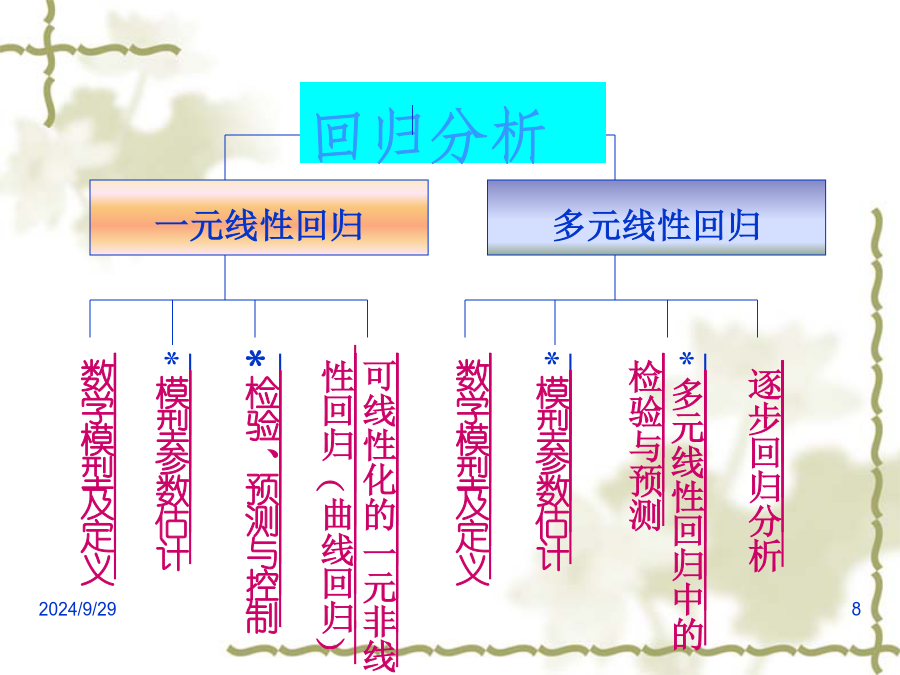
四、参数估计五、假设检验教学目的一元线性回归本讲命令2、预测和预测误差估计：非线性回归一、数学模型一元线性回归分析的主要任务是：二、模型参数估计2024/9/292024/9/29三、检验、预测与控制（Ⅰ）F检验法（Ⅲ）r检验法2、回归系数的置信区间3、预测与控制（2）控制四、可线性化的一元非线性回归
（曲线回归）散
点
图通常选择的六类曲线如下：一、数学模型及定义二、模型参数估计返回三、多元线性回归中的检验与预测2、预测四、逐步回归分析这个过程反复进行，直至既无不显著的变量从回归方程中剔除，又无显著变量可引入回归方程时为止。
统计工具箱中的回归分析命令多元线性回归3、画出残差及其置信区间：rcoplot（r，rint）例某商场一年内每月的销售收入X(万元)与销售费用Y(万元)统计如表，试求销售费用Y关于销售收入X的线性回归方程。例13、残差分析，作残差图：
rcoplot(r,rint)法一法二（二）多元二项式回归例3设某商品的需求量与消费者的平均收入、商品价格的统计数
据如下，建立回归模型，预测平均收入为1000、价格为6时
的商品需求量.在画面左下方的下拉式菜单中选”all”,则beta、rmse和residuals都传送到Matlab工作区中.在Matlab工作区中输入命令：beta,rmse结果为:b=
110.5313
0.1464
-26.5709
-0.0001
1.8475
stats=
0.970240.66560.0005非线性回归例4对第一节例2，求解如下：4、预测及作图：
[YY,delta]=nlpredci('volum',x',beta,r,J)；
plot(x,y,'k+',x,YY,'r')例5财政收入预测问题：财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。下表列出了1952-1981年的原始数据，试构造预测模型。
1．对回归模型建立M文件model.m如下:
functionyy=model(beta0,X)
a=beta0(1);
b=beta0(2);
c=beta0(3);
d=beta0(4);
e=beta0(5);
f=beta0(6);
x1=X(:,1);
x2=X(:,2);
x3=X(:,3);
x4=X(:,4);
x5=X(:,5);
x6=X(:,6);
yy=a*x1+b*x2+c*x3+d*x4+e*x5+f*x6;
2.主程序liti6.m如下:
betafit=
0.5243
-0.0294
-0.6304
0.0112
-0.0230
0.3658

即y=0.5243x1-0.0294x2-0.6304x3+0.0112x4-0.0230x5+0.3658x6

逐步回归例6水泥凝固时放出的热量y与水泥中4种化学成分x1，x2，x3，x4有关，今测得一组数据如下，试用逐步回归法确定一个线性模型.2、逐步回归：
（1）先在初始模型中取全部自变量：
stepwise(x,y)
得图StepwisePlot和表StepwiseTable（2）在图StepwisePlot中点击直线3和直线4，移去变量x3和x4（3）对变量y和x1、x2作线性回归：
X=[ones(13,1)x1x2];
b=regress(y,X)作业2024/9/294、混凝土的抗压强度随养护时间的延长而增加，现将一批混凝土作成12个试块，记录了养护日期x（日）及抗压强度y（kg/cm2）的数据：谢谢大家