
第9章 spss的相关分析和线性回归分析.ppt

qw****27









亲,该文档总共52页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

SPSS的相关分析和线性回归分析.pptx
问题第八章本章内容8.1相关分析和回归分析概述简单散点图:表示一对变量间统计关系的散点图。重叠散点图:表示多对变量间统计关系的散点图。矩阵散点图:以方形矩阵的形式在多个坐标轴上分别显示多对变量间的统计关系。以3*3矩阵散点图为例。三维散点图:以立体图的形式展现三对变量间的统计关系。对不同类型的变量应采用不同的相关系数来度量,常用的相关系数主要有Pearson简单相关系数、Spearman等级相关系数和Kendall相关系数等。8.2.2.1Pearson简单相关系数(适用于两个变量都是数值型的数据)Pea

第9章 spss的相关分析和线性回归分析.ppt
第9章spss的相关分析和线性回归分析相关分析和回归分析是统计分析方法中最重要内容之一,是多元统计分析方法的基础。相关分析和回归分析主要用于研究和分析变量之间的相关关系,在变量之间寻求合适的函数关系式,特别是线性表达式。本章主要内容:对变量之间的相关关系进行分析(Correlate)。其中包括简单相关分析(Bivariate)和偏相关分析(Partial)。建立因变量和自变量之间回归模型(Regression),其中包括线性回归分析(Linear)和曲线估计(CurveEstimation)。数据条件:参

2012下-第8章-SPSS的相关分析和线性回归分析.ppt
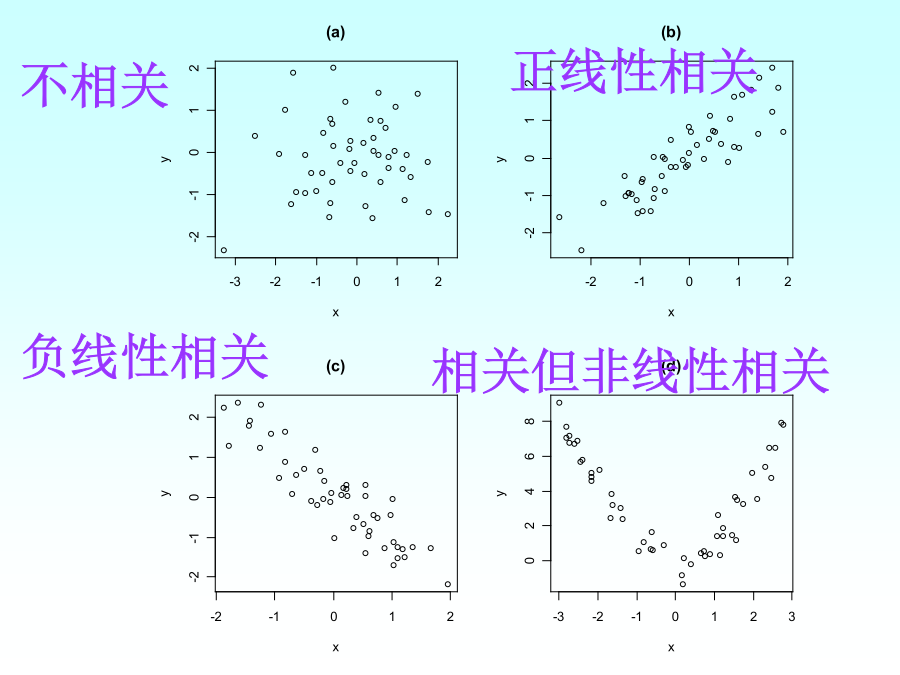
第八章SPSS的相关分析和线性回归分析8.1相关分析和回归分析概述8.2相关分析8.3偏相关分析8.4线性回归分析(重点)8.5曲线估计8.6二项Logistic回归分析8.1相关分析和回归分析概述相关分析与回归分析的区别8.2相关分析相关分析通过图形和数值两种方式,有效地揭示事物之间相关关系的强弱程度和形式。8.2.1散点图它将数据以点的的形式画在直角坐标系上,通过观察散点图能够直观的发现变量间的相关关系及他们的强弱程度和方向。散点图的绘制简单分布(SimpleScatter),只能在图上显示一对相关变

线性回归spss分析.docx
线性回归分析的具体步骤SPSS软件中进行线性回归分析的选择项为Analyze→Regression→Linear。如图3.9所示。下面通过例题介绍线性回归分析的操作过程。图3.9Regression分析功能菜单例3.仍然用例2的数据,考察火柴销售量与各影响因素之间的相关关系,建立火柴销售量对于相关因素煤气户数、卷烟销量、蚊香销量、打火石销量的线性回归模型,通过对模型的分析,找出合适的线性回归方程。解:建立线性回归模型的具体操作步骤如下:1、打开数据文件SY-9,单击AnalyzeRegressionL

SPSS的线性回归分析.ppt
第九章SPSS的线性回归分析回归分析概述回归分析概述线性回归分析概述一元线性回归分析一元线性回归方程的检验一元线性回归方程的检验一元线性回归方程的检验一元线性回归方程的检验一元线性回归方程的检验一元线性回归分析操作一元线性回归分析操作一元线性回归分析操作线性回归方程的残差分析线性回归方程的残差分析线性回归方程的残差分析线性回归方程的预测多元线性回归分析多元线性回归方程的检验多元线性回归方程的检验多元线性回归方程的检验多元线性回归方程的检验多元线性回归分析中的自变量筛选多元线性回归分析中的自变量筛选多元线性
